标签:数组 动手 逻辑 col dtree eve 理解 none 难度
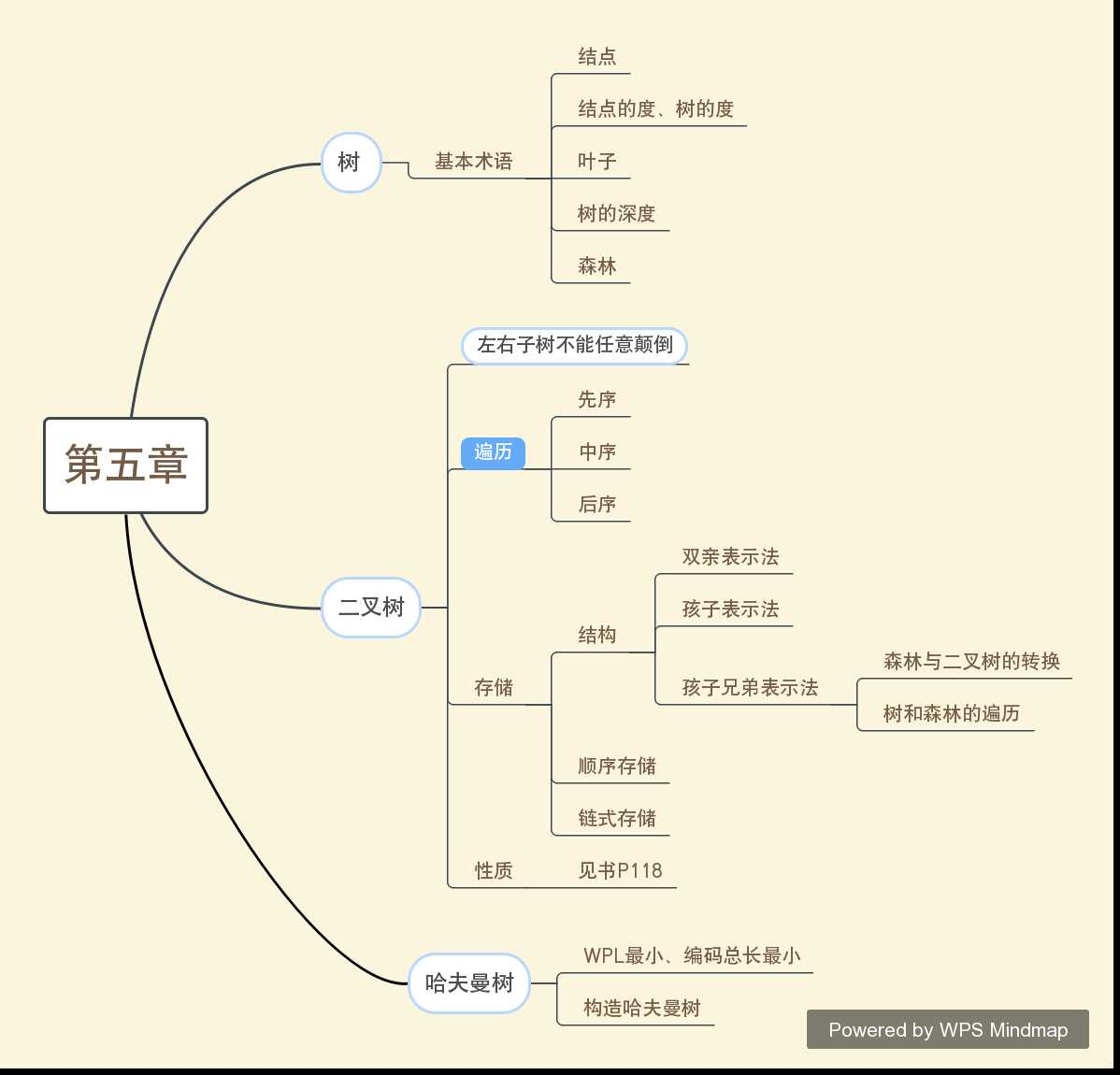
本章学习内容:
1.list leave
以下是完整代码:

1 #include <iostream> 2 #include <queue> 3 using namespace std; 4 5 typedef struct 6 {//定义结点类型 7 int left;//左孩子下标 8 int right;//右孩子下标 9 }node; 10 11 void levelOrderTraverse(node t[],int x); 12 int createBiTree(node t[]); 13 14 int main() 15 { 16 node t[10]; 17 int x; 18 x=createBiTree(t);//x为根节点 19 levelOrderTraverse(t,x); 20 } 21 22 23 24 int createBiTree(node t[]) 25 { 26 int n, i; 27 char x,y; 28 bool check[10]={false}; 29 cin>>n; 30 if(n) 31 { 32 for(i=0;i<n;i++){ 33 cin>>x>>y; 34 if(x!=‘-‘)//对左节点处理 35 { 36 t[i].left=x-‘0‘; 37 check[t[i].left]=true;//标记该结点指向了某个位置 38 } 39 else t[i].left=-1;//该节点没有孩子 40 41 if(y!=‘-‘)//对右节点处理 42 { 43 t[i].right=y-‘0‘; 44 check[t[i].right]=true;//标记该结点指向了某个位置 45 } 46 else t[i].right=-1;//没有孩子 47 } 48 for(i=0;i<n;i++){//找根节点 49 if(!check[i]) 50 return i; 51 }//返回根节点下标 52 } 53 } 54 55 void levelOrderTraverse(node t[],int x) 56 {//层次遍历 57 queue<int> q; 58 int temp; 59 int leaves=0;//标记是第几个叶子结点 60 q.push(x);//根据根节点下标入队 61 62 while(!q.empty()) 63 { 64 temp=q.front(); 65 q.pop(); 66 if(t[temp].left==-1&&t[temp].right==-1) 67 { 68 if(leaves)//第一个叶子节点不输出空格 69 cout<<" "; 70 cout<<temp; 71 ++leaves; 72 } 73 if(t[temp].left!=-1) 74 q.push(t[temp].left);//左孩子入队 75 if(t[temp].right!=-1) 76 q.push(t[temp].right); //右孩子入队 77 } 78 }
这道题中让我觉得很妙的点是buildtree中利用ASCII码将char输出成数字;除此之外主要用了队列和层次遍历来完成按层次遍历顺序输出。在处理最后一个空格的问题时,我一开始不知道要怎么标记才能最后一个空格不输出,最后用了leaves标记叶子数,第一个叶子时不输出空格。除此之外也可以用队是否为空来判断,因为最后一个数要先pop出来此时队为空,不输出空格。***createtree的时候要返回根节点,这样在遍历的时候才可以从根节点开始遍历!!!(利用了check数组,一开始全部初始化为false,没有在其他结点的左右节点出现过的就是根节点(没有被变成true的))
2.树的同构
以下是完整代码:

1 #include <iostream> 2 using namespace std; 3 #define ElemType char 4 #define MAXTREE 10 5 struct treenode 6 {//定义结点类型 7 ElemType element;//本结点数据 8 int left;//左孩子下标 9 int right;//右孩子下标 10 }T1[MAXTREE],T2[MAXTREE]; 11 12 int judge(int,int); 13 int createBiTree(struct treenode t[]); 14 int main() 15 { 16 int r1=createBiTree(T1);//r1为T1根节点下标 17 int r2=createBiTree(T2);//r2为T2根节点下标 18 if(judge(r1,r2)) cout<<"Yes"<<endl; 19 else cout<<"No"<<endl; 20 return 0; 21 } 22 23 int createBiTree(struct treenode t[]) 24 { 25 int n, i; 26 char x,y; 27 bool check[10]={false}; 28 cin>>n; 29 if(n) 30 { 31 for(i=0;i<n;i++){ 32 cin>>t[i].element>>x>>y; 33 if(x!=‘-‘)//对左节点处理 34 { 35 t[i].left=x-‘0‘; 36 check[t[i].left]=true;//标记该结点指向了某个位置 37 } 38 else t[i].left=-1;//该节点没有孩子 39 40 if(y!=‘-‘)//对右节点处理 41 { 42 t[i].right=y-‘0‘; 43 check[t[i].right]=true;//标记该结点指向了某个位置 44 } 45 else t[i].right=-1;//没有孩子 46 } 47 for(i=0;i<n;i++){//找根节点 48 if(!check[i]) 49 return i; 50 }//返回根节点下标 51 } 52 else 53 return -1; 54 } 55 56 57 int judge(int r1,int r2) 58 {//判断是否同构 59 if((r1==-1)&&(r2==-1))//两树都为空 60 return 1; 61 62 if(((r1==-1)&&(r2!=-1))||((r1!=-1)&&(r2==-1)))//其中一棵树不为空 63 return 0; 64 65 if(T1[r1].element!=T2[r2].element)//两树根不相同 66 return 0; 67 68 if(T1[r1].left==-1&&T2[r2].left==-1)//两树都没有左孩子 69 return judge(T1[r1].right,T2[r2].right);//比较右孩子 70 71 if((T1[r1].left!=-1&&T2[r2].left!=-1)&&(T1[T1[r1].left].element==T2[T2[r2].left].element))//左子树同时不为空时比较左子树的element 72 return (judge(T1[r1].right,T2[r2].right)&&judge(T1[r1].right,T2[r2].right));//比较左边和右边相等不相等 73 74 else//左子树的element不同时比较t1左子树和t2右子树,t1右子树和t2左子树 75 return (judge(T1[r1].left,T2[r2].right)&&judge(T1[r1].right,T2[r2].left)); 76 77 78 }
这道题也是利用createtree返回根节点下标,然后再从根节点开始比较两棵树是否同构。其中分情况比较两棵树是否同构让我觉得很头痛,很容易就漏掉情况,要考虑到每一种情况才能正确比较出来。在PTA上运行的时候空树的判定点一直都显示段错误,我也没有发现有什么错误,后来在别人的提醒下才发现是没有列出空树的情况要返回什么值,导致了空树的情况下是没有运行结果的。在比较是否同构时考虑不同的情况下也运用到了递归,这里就很好的体现了要停留在本层的思想。

1 int judge(int r1,int r2) 2 {//判断是否同构 3 if((r1==-1)&&(r2==-1))//两树都为空 4 return 1; 5 6 if(((r1==-1)&&(r2!=-1))||((r1!=-1)&&(r2==-1)))//其中一棵树不为空 7 return 0; 8 9 if(T1[r1].element!=T2[r2].element)//两树根不相同 10 return 0; 11 12 if(T1[r1].left==-1&&T2[r2].left==-1)//两树都没有左孩子 13 return judge(T1[r1].right,T2[r2].right);//比较右孩子 14 15 if((T1[r1].left!=-1&&T2[r2].left!=-1)&&(T1[T1[r1].left].element==T2[T2[r2].left].element))//左子树同时不为空时比较左子树的element 16 return (judge(T1[r1].right,T2[r2].right)&&judge(T1[r1].right,T2[r2].right));//比较左边和右边相等不相等 17 18 else//左子树的element不同时比较t1左子树和t2右子树,t1右子树和t2左子树 19 return (judge(T1[r1].left,T2[r2].right)&&judge(T1[r1].right,T2[r2].left)); 20 21 22 }
其中在没有左孩子时就递归比较右孩子,在左子树同时不为零时比较两左子树的元素是否相等,相等就比较左和右是否相等,不相等就看看是不是左右子树交换了
3.深入虎穴

1 #include <iostream> 2 #include <queue> 3 using namespace std; 4 typedef struct 5 { 6 int doors;//门的数量 7 int *p;//指向具体门的编号 ,把p看作是整型数组 8 }node; 9 10 int find(node *a, int root); 11 int input(node *&a); 12 13 int main() 14 { 15 node *a;//定义一个动态的整型数组 16 int i, j, k, root; 17 18 root=input(a); 19 cout<<find(a,root)<<endl; 20 21 return 0; 22 } 23 24 int input(node *&a) 25 { 26 int n, x,i,j; 27 bool *vi; 28 cin>>n; 29 a=new node[n+1];//为a数组申请空间 30 vi=new bool[n+1]; 31 for(i=1;i<=n;i++)//将vi初始化 为false 32 vi[i]=false; 33 for(i=1;i<=n;++i) 34 { 35 cin>>x; 36 a[i].doors=x; 37 a[i].p=new int[x];//有效下标为0~x-1 38 for(j=0;j<x;++j) 39 { 40 cin>>a[i].p[j]; 41 vi[a[i].p[j]]=true;//标记该门为true 42 } 43 } 44 45 for(i=1;i<=n;++i) 46 if(!vi[i]) break; 47 return i; 48 } 49 50 int find(node *a, int root) 51 {//从a数组的root下标开始往下搜索 52 int x, j; 53 queue<int> q;//定义一个用于存放待访问的门编号的队列 54 q.push(root);//根编号入队 55 while(!q.empty()){//当队列不为空: 56 x=q.front(); 57 q.pop(); 58 if(x!=0){ 59 for(j=0;j<a[x].doors;j++) 60 q.push(a[x].p[j]);//x后面的门的编号 61 } 62 }//while 63 return x;//答案就是x 64 }
这道题在课上跟着老师的步骤做,基本没有什么大的问题,但自己在写最后的find函数时还是有点点难度。这道题用了动态数组,这样可以让空间使用更加灵活。除了这种方法外,在数据量小的时候也可以直接用二维数组,通向的门标记1,不通的门标记0(门的编号就是数组下标),但是这种方法在数据量大的时候通常为稀疏矩阵,而且这道题的数据量太大了也不适合。除此之外还可以用静态链表,一个元素存门的序号,再定义一个指针,指向单链表(放通向的门)。
其中find函数部分:
1 while(!q.empty()){//当队列不为空: 2 x=q.front(); 3 q.pop(); 4 if(x!=0){ 5 for(j=0;j<a[x].doors;j++) 6 q.push(a[x].p[j]);//x后面的门的编号 7 } 8 }//while
这里当x出队时,就让x对应的门都入队,本质上其实是层次遍历。因为最后一个出队的就是最后一个进队的,也就是最深的那一个,所以x就是要找的那个
这次的三道编程题最后都顺利完成了,但是有些问题是因为不注重细节,考虑得不够完整,思维逻辑还不够严密,而且深入虎穴那道题也是跟着老师才做出来的,课下还是要自己好好消化理解,希望自己能够多看代码,多实践,能够熟练掌握树的遍历的内容,多看看哈夫曼树的内容,也要动手自己画一下分析一下!:D
标签:数组 动手 逻辑 col dtree eve 理解 none 难度
原文地址:https://www.cnblogs.com/liulijun1551/p/10807277.html