标签:基本操作 info 提高 .com 出现 一个 div 判断 建立
一、树的实践应用
(近两周系统地学习了树的基本操作知识。但是在完成实际应用的时候,发现知识的迁移能力还是有待提高)
(1)树的遍历的选择,是否使用递归。
对于list leaves(寻找叶子结点)的题目中,基于遍历方式的选择有不同的结果。
(a)使用:递归——先序:
前提:
a是存储结点的数组,每个结点有两个成员,左右孩子的下标。
typedef struct
{
int lc;
int rc;
}node;
实现代码:
void find(node a[],int x)//
{
if(x!=-1)
{
if(a[x].lc==-1 &&a[x].rc==-1)
{
leaves[n]=x;
}
else
{
find(a,a[x].lc);
find(a,a[x].rc);
}
}
(b)使用:while循环——层次遍历;特点:叶子结点即为孩子下标下标均为“-1”的
以下是5.5作业(树)的7-1list leaves中的节选代码:
法一:左右孩子需要判断“-1”
或者法二:与法一区别于对空结点的判断的顺序:每一次都判断是否为“-1”
void find(node a[],int x)//层次遍历基于数组的二叉树
{
int tmp;
queue<int> q;
q.push(x); //根结点所在下标入队
int print[10],n=0;
while(!q.empty())
{
tmp=q.front();//用于临时存放二叉树根结点
q.pop();
if(a[tmp].lc==-1&&a[tmp].rc==-1)
{
print[n]=tmp;//满足叶子结点的条件,用一个数组存放
n++;
}
if(a[tmp].lc!=-1)
{
q.push(a[tmp].lc);
}
if(a[tmp].rc!=-1)
{
q.push(a[tmp].rc);
}
}
cout<<print[0];
for(int k=1;k<n;k++)
{
cout<<" "<<print[k];
}
}
(2)建立树的方法:
以结点结构体为元素类型的数组:
1、结构体包括该结点数据孩子data、孩子结点的下标:
typedef struct
{
int data;
int lc;
int rc;
}node;
2、结构体包括该结点数据孩子data、含有未知孩子个数的下标的数组首地址:
typedef struct
{
int doors;
int *p;//由于有未知的孩子个数,建立数组
}node;
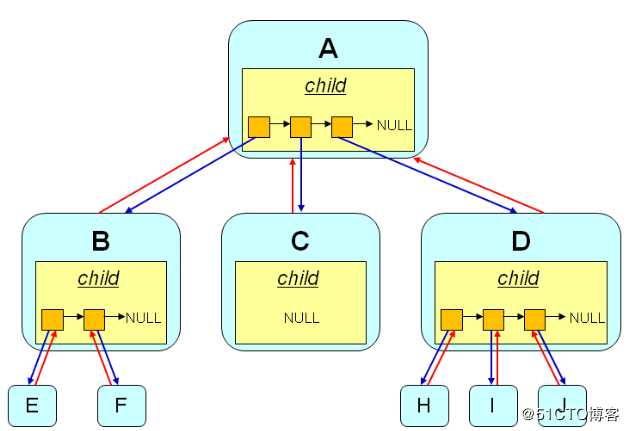
二、哈夫曼树
目的:编码最短最优。
创建哈夫曼树原理:
结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和,通常记作WPL。
创建哈夫曼树步骤:
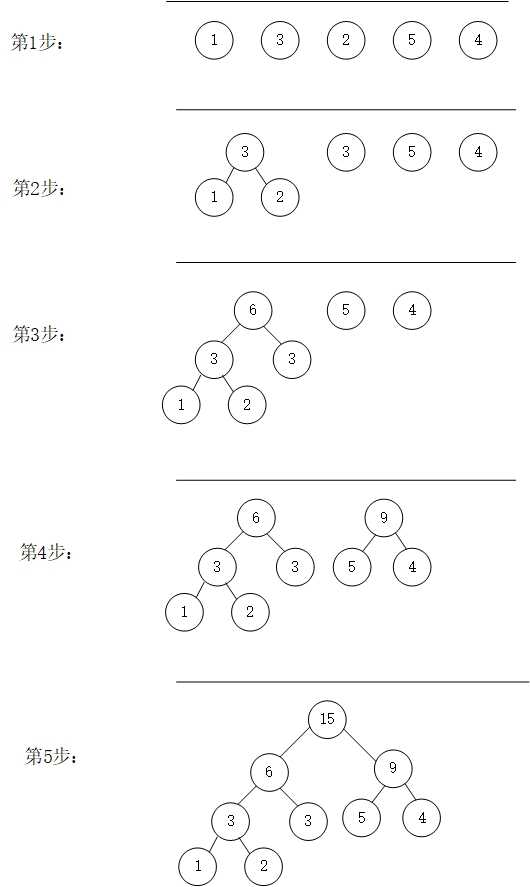
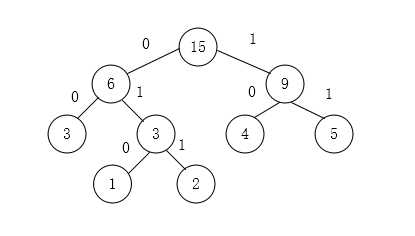
图来自https://www.cnblogs.com/sench/p/7798064.html
由此出现频率最高的离跟最近,最短编码得以求解。
二、目标完成程度,下阶段目标
对于树的实际应用和课本知识的迁移还需要多加练习,每日代码只完成50%。
下阶段需要加强对“段错误”“超限”等问题的分析的总结。
每日代码仍需努力。
标签:基本操作 info 提高 .com 出现 一个 div 判断 建立
原文地址:https://www.cnblogs.com/gzq18/p/10808767.html