第五章数据结构总结

标签：nbsp   ==   灵活   lse   iso   image   一个   mamicode   顺序   

实践第一题的一段代码

int Isomorphic(int root1,int root2)
   {   //用递归结构判断
    if(root1==-1 && root2==-1)    
    return 1;       //若都为空树，则同构
    if((root1==-1 && root2!=-1) || (root1!=-1 && root2==-1))
       return 0;      //一颗为空，一颗不为空则不同构
    if(t1[root1].name!=t2[root2].name)
      return 0;       //第一层数据不相等，不同构
    if(t1[root1].lch==-1 && t2[root2].rch==-1) //如果左孩子都为空  
      return( Isomorphic(t1[root1].rch,t2[root2].rch));   //判断右孩子是否为空，数据是否相等，是否一个有右孩子，一个没有
 
 if((t1[root1].lch!=-1) && (t2[root2].lch!=-1) && (t1[t1[root1].lch].name==t2[t2[root2].lch].name)) 
        return ( Isomorphic(t1[root1].lch,t2[root2].lch) && Isomorphic(t1[root1].rch,t2[root2].rch ) ) ;
    else
    return( Isomorphic( t1[root1].lch,t2[root2].rch ) && Isomorphic( t1[root1].rch,t2[root2].lch ) )
 ;}

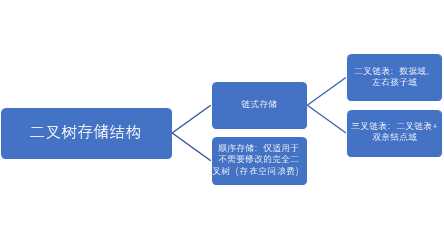
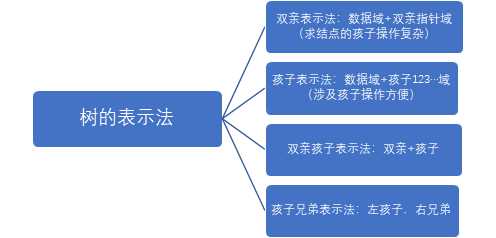
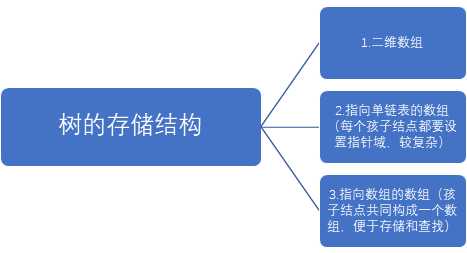
在这一章学习中我们学会了如何用多种顺序遍历一棵二叉树，如何查找根结点，并在老师的带领下学会如何让进一步分析树的最方便的存储结构.但有时运用的不够灵活，比如知道一个完全二叉树的结点数，还能反过来推出他的深度，作业中就有一题说到一个二叉树有65个节点，也就是2的6次方加一，所以一共有七层，虽然感觉学到了一丢丢但感觉作业还是有很多还没弄懂，要继续加油.

第五章数据结构总结

标签：nbsp   ==   灵活   lse   iso   image   一个   mamicode   顺序   

原文地址：https://www.cnblogs.com/gjhhaidouS/p/10817191.html