标签:blank plot 代码实现 eid 维度 子矩阵 测试 简单 time
这个是本人在做大创项目,师姐做完的特征提取部分代码后,我们利用接收到的结果进行特征选择操作。下面从要求和思路两个部分简单介绍一下:我们通过BPSO结合KNN进行降维的基本思路。
一、要求
学姐给我们的数据一共有4个.mat文件。分别是训练集数据、训练集标签、测试集数据和测试集标签。训练集和测试集分别是60张图片,每张图片提取了1862个特征。因此,我们得到的Train_dataH和Test_data都是60*1862的阵列,标签为60*1的列矩阵。我们观察了标签,发现训练集和测试集都分别是10类,每一类都是6个。对于拿到的数据,我猜想应该是有60张照片,然后一共有10个人,每个人6张照片。
学姐给我们的要求是,让我们通过算法,选择特征,我们的首要任务是,通过算法删减掉了冗余特征以后,算法识别准确率得到提升。如果在准确率难以得到改善的情况下,我们应尽可能减少特征数。
所以,我们的目标是:1.提升准确率2.实现进一步降维。
二、基本思路
1.提高准确率即减少错误率,降维即减小特征数。我将这个问题定性为组合优化。优化问题中,可以利用启发式智能算法进行处理。在该问题中,显然是离散类问题,我们针对性的使用二进制粒子群算法。由于我们有两个目标,所以,这是双(多)目标优化。为了简单起见,我们通过线性组合的方式,同时将错误率和降维后的特征数组合在一个适应度函数里。
2.所谓降维,即删除冗余特征,哪怕是不删除,也应当在操作中剔除不予以不考虑。由于共有1862维,我的考虑是,最终对于这些数据,从每一维数据的角度来看也就是删除或保留两种情况。这样就好办了,我们利用0/1来表示我们要删除或是保留该特征。如果我们从宏观上来理解,1862个特征,取与不取,在总体解空间里,会有21862组解。但是显然我们不可能利用暴力枚举法去寻找到最合适的解的情况,因为这明显超出了我们所能承受的时间复杂度,因此,“退而求其次”的启发式算法可以大显身手。启发式算法的定义如下:一个基于直观或经验构造的算法,在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每一个实例的一个可行解,该可行解与最优解的偏离程度一般不能被预计[1]。我们设定了300个粒子,每一个粒子长1862。因此对于粒子矩阵x,它是(N=300)*(D=1862)维的矩阵。矩阵中的每一个元素取值非0即1.xij代表的是第i个粒子粒子,在第j个特征下取或不取。我们通过这300个粒子在解空间中不断迭代更新,找到每一个粒子的个体最优解pbest,在个体最优找到的情况下,搜寻全体最优gbest。经过一次迭代以后会有一个gbest。我们利用gb来进行标记每次迭代后的gbest的值。在经过T次的迭代以后,我们就能够得到T次迭代下的适应度函数变化情况,我们可以以函数图像方式将其呈现出来。
3.对于适应度函数,我们在第1点中也有提到。我们利用错误率与降维后的特征数的线性组合来定义适应度函数,使得两者能够同时得到较好结果。由于准确率显然更重要,所以,我们将准确率权值设置为0.8,而将后者设置为0.2.
适应度函数表达式如下:
fitness=ERRORRATE*0.8+DIMENSION/D*0.2
(1)ERRORRATE:错误率来源于分类结果,分类结果来源于分类器。这里,我们利用KNN进行分类。
对于KNN代码,我们直接利用matlab自带函数进行求取。在求取过程中,需要注意我们有对特征进行选取的操作。也就是说如果我们不取的特征在比较求解汉明距离时就应当考虑到。我们通过将x的每一维与每一张图片的1862个特征的每一维相乘,如果在该维不取,即x为0,在相乘过程中,相应位的训练集和测试集数据都将被置0.在求解距离时也为0,则不受到影响,达到降维效果。我们将distancetraindata和distancetestdata分别定义为数据经过第i个粒子降维后的矩阵,将这两个矩阵进行knn分类,计算分类识别的准确率。
(2)DIMENSON:其为第i个粒子所取特征数,只需记录x矩阵第i行有多少个1即可。
三、代码实现
main.m
clear all;
close all;
clc;
load TrainData1.mat
load TrainLabels1.mat
load testData1.mat
load testLabels1.mat
Train_data = TrainData1 ;%归一化以后的训练集数据
Train_lable = TrainLabels1 ;%将训练集标签导入
Test_data = testData1 ;%归一化后的测试集数据
Test_lable = testLabels1;%将测试集标签导入
%%
%数据赋值
N=300;% 粒子数随机设定为300个
D=1862;% 粒子维度为1862
T=20;% 迭代次数设定为2,快速查看结果
c1=1.5;% 学习因子均设为1.5
c2=1.5;
Wmax=0.8;% 惯性权重随着迭代次数增加进行更改
Wmin=0.4;
Vmax=10;% 粒子速度设定为+-10范围内
Vmin=-10;
%%
%思路:
%粒子群算法在本题内实现降维功能
%设定N个粒子,每一个粒子D维,每一维是否为1/0,代表这一个特征取与不取
%最终反应到g上表示全局最优情况下每一维取或不取
%%
%初始化
%初始化种群个体
x=randi([0,1],N,D);% 设定x每一个粒子的每一维上为0/1
v=rand(N,D)*(Vmax-Vmin)+Vmin;%速度取随机
%初始化个体、全局最优极值及其初始位置
p=x;
pbest=ones(N,1);
g=ones(1,D);
gbest=1000000;
%个体极值初始化
for i=1:N
pbest(i)=bpso_project(x(i,:),Train_data , Train_lable , Test_data , Test_lable);
end
%全局极值初始化
for i=1:N
if(pbest(i)<gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%%
%迭代更新
for i=1:T %以下为每次迭代情况
for j=1:N %对于每一个粒子而言
%更新个体最优值机器位置
if(pbest(j)>bpso_project(x(j,:),Train_data , Train_lable , Test_data , Test_lable))
p(j,:)=x(j,:);
pbest(j)=bpso_project(x(j,:),Train_data , Train_lable , Test_data , Test_lable);
end
%更新全局最优值及其位置
if(pbest(j)<gbest)
g=p(j,:);
gbest=pbest(j);
end
%计算动态惯性权重
w=Wmax-(Wmax-Wmin)*i/T;
%更新位置和速度值
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
%边界处理
for ii=1:D
if(v(j,ii)>Vmax|v(j,ii)<Vmin)
v(j,ii)=rand*(Vmax-Vmin)+Vmin;
end
end
vx(j,:)=1./(1+exp(-v(j,:)));
for jj=1:D
if vx(j,jj)>rand
x(j,jj)=1;
else
x(j,jj)=0;
end
end
end
%记录历代全局最优值
gb(i)=gbest;
end
%%
%经过运算以后的特征数
DIMENSION=sum(g);
%%
%准确率
acc=100-(gb-0.2*WeiDu/D)/80
%%
%适应度变化曲线
figure(1);
plot(gb);
xlabel(‘迭代次数‘);
ylabel(‘适应度值‘);
title(‘适应度变化曲线‘);
%%
%看一看降维效果
figure(2);
R=x;
for m=1:N
for n=1:D
R(m,n)=x(m,n)*g(1,n);
end
end
imshow(R);
bpso_project.m
function fit = bpso_project(x,Train_data , Train_lable , Test_data , Test_lable) D=1862; TIME=sum(x); accuracy=myknn_func(x,Train_data,Train_lable,Test_data,Test_lable); fit=(100-accuracy)/100*0.8+TIME/D*0.2;
myknn_func.m
function accuracy=myknn_func(x,traindata,trainlabel,testdata,testlabel)
Distance=zeros(60,60);%每一行存储的是一个测试样本与所有训练样本的距离
%%
%利用汉明距离来计算两个样本的差距
distancetestdata=zeros(60,1862);
distancetraindata=zeros(60,1862);
for i=1:60
for j=i:1862
distancetestdata(i,j)=testdata(i,j)*x(1,j);%如果在某一维上不去,则将该维所有的训练集与测试集样本置0存入新变量中,利用新变量计算汉明距离
distancetraindata(i,j)=traindata(i,j)*x(1,j);%如此一来,对于测试集与训练集数据没有任何变化
end
end
Distance=pdist2(distancetestdata,distancetraindata,‘hamming‘); %此为计算汉明距离
%%
%KNN分类实现
mdl = ClassificationKNN.fit(distancetraindata,trainlabel,‘NumNeighbors‘,1);
predict_label = predict(mdl, distancetestdata);
accuracy = length(find(predict_label == testlabel))/length(testlabel)*100
运行结果如下:
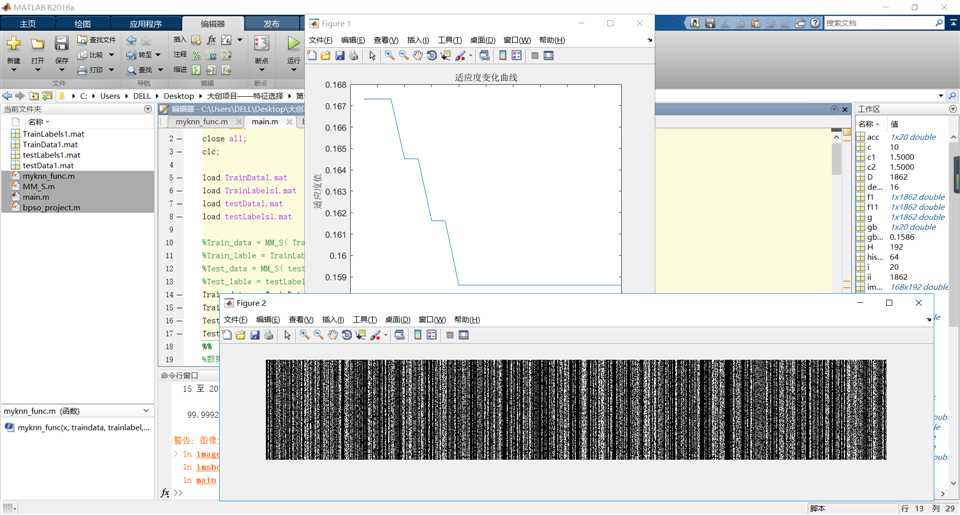
经过计算,维度是856.,准确率达到了99.9992%。
参考文献:
[1]https://baike.baidu.com/item/%E5%90%AF%E5%8F%91%E5%BC%8F%E7%AE%97%E6%B3%95/938987?fr=aladdin
2019-05-08
18:41:23
标签:blank plot 代码实现 eid 维度 子矩阵 测试 简单 time
原文地址:https://www.cnblogs.com/lyxyhhxbk/p/10833679.html