码迷，mamicode.com
首页 > 其他好文 > 详细

各种友(e)善(xin)数论总集（未完待续），从入门到绝望

时间：2019-05-11 10:56:31      阅读：122      评论：0      收藏：0      [点我收藏+]

标签：方程组   solution   裴蜀定理   位置   +=   problem   sizeof   href   \n   

目录

@

快速幂

题目描述
【题意】
求a^b mod c，a,b,c都是整数。
【输入格式】
一行三个整数 a、b、c。 0 ≤ a,b,c ≤ 10^9
【输出格式】
一行，a^b mod c的值。
【样例输入】
2 5 7
【样例输出】
4

题目链接就不放出来了，因为这个OJ已经很卡了，且不登录不能看题目。

其实，我们容易知道，幂次有个性质：当\(b\%2==0\)时\(a^{b}=(a*a)^{b/2}\)

用脑子想想就知道。

#include<cstdio>
#include<cstring>
using  namespace  std;
typedef  long  long  LL;
LL  kms(LL  a,LL  b,LL  c)//a^b%c
{
    LL  ans=1%c;/*防止c==1*/a%=c;
    while(b)//b!=0
    {
        if(b&1)ans=(ans*a)%c;
        a=(a*a)%c;b>>=1;//b/=2;
    }
    return  ans;
}
int  main()
{
    LL  a,b,c;scanf("%lld%lld%lld",&a,&b,&c);
    printf("%lld\n",kms(a,b,c));
    return  0;
}

扩展欧几里得

GCD

如果我们要求两个数字的最大公约数怎么求？

如果两个数字\(a,b\)存在最大公约数\(k\)，那么把\(a\)写成\(xk\)，把\(b\)写成\(yk\)

那么我们知道\(b\%a=(y\%x)k\)，但是\(y\)又与\(x\)互质，所以仅当\(x=1\)时，\(y\)为最大公约数，此时\(a=k\)也就是最大公约数，而且我们也知道\(y\%x\)也是与x互质的。

所以我们可以设新的\(a'\)与新的\(b'\)，\(a'=b\%a\),\(b'=a\)，当\(a'=0\)时，\(b\)就是最大公约数。

而且一开始\(a>b\)也不怕，做了一次交换后就换过来了(\(b\%a=b\))

int  gcd(int  x,int  y)
{
    if(x==0)return  y;
    return  gcd(y%x,x);
}

扩展欧几里得

如何求\(ax+by=c\)的一个整数解？

尽看扩展欧几里得。

首先，我们设\(ax+by=gcd(a,b)\)

那我们就想了，如果有个方程为\(0x+gcd(a,b)y=gcd(a,b)\)，不就很妙了吗？
\(y=1,x\)随便等于什么都不影响最终结果，只不过一般取0，怕爆long long。

然后我们再证一个：

当我们解出了\((b\%a)x+ay=gcd(a,b)\)，怎么推到\(ax+by=gcd(a,b)\)？

我们可以推导一下(\(?x?\)为向下取整)：
\[ax+by=(b-?b/a?*a)x'+ay'\]
\[ax+by=-a*?b/a?x'+ay'+bx'\]
\[ax+by=a(y'-?b/a?x')+bx'\]

而\(?b/a?\)就是C++的\(b/a\)

所以，我们发现\(b\%a\)和\(a\)就是\(gcd\)过程，所以最后也会得到\(0\)和\(gcd(a,b)\)

然后再看：如果\(gcd(a,b)|c\)的话，设\(d=c/gcd(a,b)\)，然后把\(x,y\)直接乘以\(d\)就没什么毛病了。

但是如果不整除就无解，我们又可以证一证：

首先\(gcd(a,b)|c\)是肯定有解的，我们可以知道，而且\(ax+by=c\)可以类似于\(ax≡c\mod b\)，我们可以根据同余的性质得出我们可以把\(a,b,c\)的同一个因数\(gcd(a,b)\)提出，得到\(a',b',c'\)，化成\(a'x≡c'\mod b'\)，而且a‘与b‘不互质，那么我们可以得出，同余方程\(ax≡c\mod b\)，\(a,b\)互质时有解，或者当\(c\)整除\(gcd(a,b)\)时有解。（好像说偏了）

然后，如果\(gcd(a,b)\)与c不整除，我们再设\(z=gcd(a,b),c=kz+d\)

那么我们把原式化为：\(a'zx+b'zy=kz+d\)同除\(z\)可得

\(a'x+b'y=k+ \frac{d}{z}\)

但是\(d<z\)所以\(\frac{d}{z}\)是个分数，但是\(a'x+b'y\)都是整数，所以无解

至此，结束了（感觉又过了一个世纪）！

#include<cstdio>
#include<cstring>
using  namespace  std;
typedef  long  long  LL;
LL  exgcd(LL  a,LL  b,LL  &x,LL  &y/*引用*/)
{
    if(a==0)
    {
        x=0;y=1;//0x+gcd(a,b)y=gcd(a,b) 
        return  b;
    }
    else
    {
        LL  tx,ty;
        LL  d=exgcd(b%a,a,tx,ty);
        x=ty-(b/a)*tx;//公式 
        y=tx;//公式 
        return  d;
    }
}
int  main()
{
    LL  a,b,c,x,y;scanf("%lld%lld%lld",&a,&b,&c);
    LL  d=exgcd(a,b,x,y);
    if(c%d!=0)printf("no solution!\n");
    else
    {
        c/=d;
        printf("%lld %lld\n",x*c,y*c);
    }
    return  0;
}

其实也没什么难度。

同余系列

同余方程

题目描述

【题意】
已知a,b,m,求x的最小正整数解，使得ax≡b(mod m)
【输入格式】
一行三个整数 a，b，m。 1 ≤ a,b,m ≤ 10^9 
【输出格式】
一行一个整数x，无解输出"no solution!"
【样例输入】
2 5 7
【样例输出】
6

我们会发现\(ax≡b\)(\(mod\) \(m\))其实就是\(ax-my=b\)也就是\(ax+my=b\)（\(m\)的正负无多大必要，反正只是求\(x\)，而且\(m>0\)方便的地方在于\(gcd\)为正数）

然后我们运用扩展欧几里德求出\(x\)，但是如何求出最小的\(x\)？

学过不定式的人都知道，当\(ax\)减\([a,b]\)时，\(my\)也可以相应的加\([a,b]\)时（\([a,b]\)就是\(a,b\)的最小公倍数），\(x,y\)能得出另外一组整数解，也就是\(x-[a,b]/a,y+[a,b]/b\)，又因为\([a,b]=a*b/(a,b)\)，所以就是\(x-b/(a,b),y-a/(a,b)\)（\((a,b)\)是\(gcd(a,b)\)）。

而且\([a,b]\)是能同时被\(a,b\)整除的最小的数字。

所以，我们可以用\(d=gcd(a,b),x=(x\%(b/d)+b/d)\%(b/d)\)得出\(x\)最小的正整数解

#include<cstdio>
#include<cstring>
using  namespace  std;
typedef  long  long  LL;
LL  exgcd(LL  a,LL  b,LL  &x,LL  &y)
{
    if(a==0)
    {
        x=0;y=1;
        return  b;
    }
    else
    {
        LL  tx,ty;
        LL  d=exgcd(b%a,a,tx,ty);
        x=ty-(b/a)*tx;
        y=tx;
        return  d;
    }
}
LL  zbs(LL  x){return  x<0?-x:x;}
int  main()
{
    LL  a,b,c,x,y;scanf("%lld%lld%lld",&a,&c,&b);
    LL  d=exgcd(a,b,x,y);//求扩展欧几里得 
    if(c%d!=0)printf("no solution!\n");
    else
    {
        c/=d;
        x*=c;
        LL  k=b/d;
        x=((x%k)+k)%k;//最小的正整数解 
        printf("%lld\n",x);
    }
    return  0;
}

同余方程组

题目描述

【题意】 
同余方程是这样的：已知a,b,n,求x的最小正整数解，使得ax=b(mod m)
同余方程组是这样：也是求x的最小正整数解，但已知b数组和m数组的情况下，
x=b[1](mod m[1]),
x=b[2](mod m[2]),
x=b[3](mod m[3]),
~~~~~~
x=b[n](mod m[n])
【输入格式】
一行一个整数 n（1<=n<=?)
下来n行每行两个整数b[i]，m[i]。 1 ≤b[i],m[i] ≤ 10^9 
【输出格式】
一行一个整数x，无解输出"no solution!"
【样例输入】
3
3 5
2 3
2 7

【样例输出】
23

这道题就十分的友(e)善(xin)了

现在我们可以列出\(x=b_{1}+m_{1}y_{1},x=b_{2}+m_{2}y_{2}...\)

我们拿上面减下面的出：\(m_{1}y_{1}-m_{2}y_{2}=b_{2}-b_{1}\)也就是\(ax+by=c\)的形式。

那么我们写成\(ax'+by'=c,a=m_{1},b=m_{2}\)（这里是\(-m_{2}\)也无所谓，但是是正数后面算最小正整数比较方便。）\(,c=b_{2}-b_{1},x'=y_{1},y'=y_{2}\)。

然后解出\(x'\)，将\(x'\)带入\(x=b_{1}+ax'\)得出了\(x\)的其中一个解，而且我们又知道\(x\)要变只能加上或减去\(b/(a,b)\)，所以\(x\)就只能加减\((b/(a,b)*a=[a,b])\)，所以我们又可以列出一个新的方程：\(x≡b_{1}+ax'\)(\(mod\) \([a,b]\))（其中的\(b_{1}+ax'\)表示的是x的其中一组解），为了后面的方便，我们把这个方程代替为第二个方程，后面就是个二三做一次，三四做一次...

然后我们就可以拿这个方程与第三个方程做这种事，重复如此，最后的\(b_{?}\)就是答案，但是，别忘了是求最小整数解。

求最小整数解有两种方法：

我常用的方法：

开局直接把每个\(b_{i}\)（不包括求出来的\(b_{?}\)）模\(a_{i}\)，并且把每次求出的\(x\)都做一次最小整数解，那么得出来的新的方程的\(b_{?}\)一定小于新的\(m_{?}\)，为什么，\(m_{?}\)为\([a,b]\)，而\(b{?}\)为\(b_{i}+ax\)得出的。（这里的\(a\)表示\(m_{i}\)，\(b\)表示\(m_{i+1}\)），我们知道\(x≤b/(a,b)-1\)，那么\(ax≤[a,b]-a\)，\(b_{i}<a\)，那么\(ax+b_{i}<[a,b]\)，所以\(b_{?}\)小于\(m_{?}\)，也就是不用模了。

#include<cstdio>
#include<cstring>
using  namespace  std;
typedef  long  long  LL;
LL  exgcd(LL  a,LL  b,LL  &x,LL  &y)
{
    if(a==0)
    {
        x=0;y=1;
        return  b;
    }
    else
    {
        LL  tx,ty;
        LL  d=exgcd(b%a,a,tx,ty);
        x=ty-(b/a)*tx;
        y=tx;
        return  d;
    }
}
LL  a1,b1;
bool  solve(LL  a2,LL  b2)
{
    LL  a=a1,b=a2,c=b2-b1,x,y;
    LL  d=exgcd(a,b,x,y);
    if(c%d!=0)return  false;
    else
    {
        c/=d;
        x*=c;
        LL  lca=b/d;
        x=((x%lca)+lca)%lca;//最小正整数解 
        b1=a1*x+b1;a1=a*b/d;//不用模 
        return  true;
    }
}
int  main()
{
    int  n;scanf("%d",&n);
    scanf("%lld%lld",&b1,&a1);b1%=a1;//开局模一模 
    for(int  i=2;i<=n;i++)
    {
        LL  a,b;scanf("%lld%lld",&b,&a);b%=a;//开局模一模 
        if(!solve(a,b))
        {
            printf("no solution!\n");
            return  0;
        }
    }
    printf("%lld\n",b1/*不用模*/);
    return  0;
}

但是后面，我又发现了一个不是很麻烦的方法，就是结尾模一下就行了。。。

//少了去正过程，中间会有许多数字变成负数
//而且更容易爆long long
#include<cstdio>
#include<cstring>
using  namespace  std;
typedef  long  long  LL;
LL  exgcd(LL  a,LL  b,LL  &x,LL  &y)
{
    if(a==0)
    {
        x=0;y=1;
        return  b;
    }
    else
    {
        LL  tx,ty;
        LL  d=exgcd(b%a,a,tx,ty);
        x=ty-(b/a)*tx;
        y=tx;
        return  d;
    }
}
LL  zbs(LL  x){return  x<0?-x:x;}
LL  a1,b1;
bool  solve(LL  a2,LL  b2)
{
    LL  a=a1,b=a2,c=b2-b1,x,y;
    LL  d=exgcd(a,b,x,y);
    if(c%d!=0)return  false;
    else
    {
        c/=d;
        x*=c;//可能为负数 
        b1=a1*x+b1;a1=a*b/d;
        return  true;
    }
}
int  main()
{
    int  n;scanf("%d",&n);
    scanf("%lld%lld",&b1,&a1);
    for(int  i=2;i<=n;i++)
    {
        LL  a,b;scanf("%lld%lld",&b,&a);
        if(!solve(a,b))
        {
            printf("no solution!\n");
            return  0;
        }
    }
    LL  zhl=a1<0?-a1:a1;//绝对值 
    printf("%lld\n",(b1%zhl+zhl)%zhl/*尾巴模一模*/);
    return  0;
}

以上便是作者的心得。

一点想法

当然，如果\(x\)前面也有系数怎么办？我们求出的值可能不能整除于\(x\)的系数？

在我们求完时，我们得到的最后一个方程就是结果。（这里为方便直接把\(b_{n}\)叫\(b\)，\(m_{n}\)叫\(m\)）

\(ax≡b\)(\(mod\) \(m\))

\(a\)什么时候是整数？

是不是当\(my+b≡0\)(\(mod\) \(a\))的时候？（\(y\)为任意整数）

那么我们解出这个方程的\(y\)的最小整数解就行了。

当然，这只是本蒟蒻的一点点假设，并没有实践过。

高次同余方程

BSGS

【题意】
求解 A^x=B(mod C)  （0<=x<C）,求x的值。
已知:C、A、B都是正整数，2 <= C < 2^31, 2 <= A < C, 1 <= B < C。
(A与C互质)
【输入格式】
多组测试数据。
每组数据一行三个整数：C，A，B。
【输出格式】
每组数据一行，如果有解输出x的最小正整数解，否则输出"no solution!"。
【样例输入】
5 2 1
5 2 2
5 2 3
5 2 4
5 3 1
5 3 2
5 3 3
5 3 4
5 4 1
5 4 2
5 4 3
5 4 4
12345701 2 1111111
1111111121 65537 1111111111
【样例输出】
0
1
3
2
0
3
1
2
0
no solution!
no solution!
1
9584351
462803587

\(BSGS\)，又名北上广深。

你是不是觉得这个东西十分的高大上？

其实还挺简单的QAQ。

我们知道\(A^{x}≡B\mod C\)

我们设\(m≡ceil(\sqrt c)\)（\(ceil\)向上取整，在C++的cmath库内）

为什么是\(ceil\)，学完你就知道了。

那么\(x\)可以写成\(ma-b\)的形式

也就是\(A^{ma-b}≡B\mod C\)

推导一波：

\[A^{ma-b}≡B\mod C\]

\[A^{ma}*A^{-b}≡B\mod C\]

\[A^{ma}≡B*A^{b}\mod C\]

出现了点倪端了，不知道大家有没有学过欧拉定理？

\(a^{φ(p)}≡1\mod p\)（当\(a\)与\(p\)互质的，\(φ(p)\)为欧拉函数，后面会讲）

所以\(x\)最大为\(φ(p)\)，为了方便，我们不在\(φ(p)\)来找，而是在\(p(p>φ(p))\)里面找，因为是找最小的，所以在两个范围找都没事，但\(p\)更方便。

当然，这里你得会Hash表（map也可以，或者像我们机房的一个大佬，不会Hash表，但会SBT）。

然后，我们枚举\(b\)从\(0\)到\(m\)，并把\(B*A^{b}\mod C\)放进Hash表，然后在枚举\(a\)从\(1\)到\(m\)，在Hash表里面找到最大的\(b\)（为了求最小的\(x\)）满足\(A^{ma}≡B*A^{b}\mod C\)，那么就可以返回答案了。

而且\(a\)从\(1\)开始，可以让\(ma≥b\)，不会出现负数，并且可以很好的枚举从\(0\)到\(C\)的所有数字。

#include<cstdio>
#include<cstring>
#include<cmath>
#define  N  2800000
using  namespace  std;
typedef  long  long  LL;
class  hash
{
    public:
        struct  node
        {
            LL  c;int  x,next;
        }a[N];int  last[N],len,h;
        hash(){h=2750159;/*用线性筛筛出的素数*/}
        void  ins(int  x,LL  c){LL  y=c%h;len++;a[len].x=x;a[len].c=c;a[len].next=last[y];last[y]=len;}
        int  find(LL  c)
        {
            LL  x=c%h;
            for(int  k=last[x];k;k=a[k].next)
            {
                if(a[k].c==c)return  a[k].x;//求最大的b 
            }
            return  -1;
        }
        void  clear(){memset(last,0,sizeof(last));len=0;}
}zjj;
LL  kms(LL  a,LL  b,LL  c)//快速幂 
{
    LL  ans=1%c;a%=c;
    while(b)
    {
        if(b&1)ans=(ans*a)%c;
        a=(a*a)%c;b>>=1;
    }
    return  ans;
}
LL  bsgs(LL  a,LL  b,LL  c)
{
    zjj.clear();
    LL  d=ceil(sqrt(c));
    LL  now=b;
    for(int  i=0;i<=d;i++)
    {
        zjj.ins(i,now);
        now=(now*a)%c;
    }//枚举b 
    LL  lim=now=kms(a,d,c);
    for(int  i=1;i<=d;i++)
    {
        int  x;
        if((x=zjj.find(now))!=-1)return  i*d-x;
        now=(now*lim)%c;
    }//枚举a 
    return  -1;
}
int  main()
{
    LL  a,b,c;
    while(scanf("%lld%lld%lld",&c,&a,&b)!=EOF)
    {
        int  ans=bsgs(a,b,c);
        if(ans==-1)printf("no solution!\n");
        else  printf("%d\n",ans);
    }
    return  0;
}

exBSGS

我们会发现上面的过程有一个限制，就是\(A,C\)必须互质，不是，这就太苛刻了吧，毒瘤出题人会有歪念头的！

于是，我们想到了同余的性质：\(a≡b\mod c\)，当\(a,b,c\)有同一个公因子\(d\)时，可以把\(d\)消掉，得出\(\frac{a}{d}≡\frac{b}{d}\mod \frac{c}{d}\)，那么，我们也可以把\(A,C\)的最大公因数提出呀，但是\(B\)也必须要整除于这个最大公因数，否则就是无解的，很容易想，我们设\(A,C\)的最大公因数为\(D\)，然后原式就等于\(\frac{A}{D}A^{x-1}≡\frac{B}{D}\mod \frac{C}{D}\)如果\(A\)与\(\frac{B}{D}\)还是不互质，我们就继续，我们设\(A\)的系数为\(K\),那么\(K\)就在此过程中不断增加，且\(x\)减的也越来越多。

当然，此过程存在一个恶心的特判，就是当\(B=K\)时，直接返回现在提了几次最大公因数，也就是\(x\)减了多少。

那么，最后，我们只需要计算\(A^{x-i}\mod C'\)的时候再乘\(K\)就行了，然后算出\(x-i\)后再加上\(i\)就行了。

一道不错的恶心的例题

这也是我在\(luogu\)对的第一道黑题（虽然插头DP也很多，但没交）

#include<cstdio>
#include<cstring>
#include<cmath>
#define  N  210000
using  namespace  std;
typedef  long  long  LL;
class  Hash//class多好用啊
{
    public:
        struct  node
        {
            int  x,next;LL  c;
        }a[N];int  len,last[N];LL  h;
        Hash(){h=200043;}
        void  ins(int  x,LL  c){LL  y=c%h;a[++len].x=x;a[len].c=c;a[len].next=last[y];last[y]=len;}
        void  clear(){len=0;memset(last,0,sizeof(last));}
        int  find(LL  c)
        {
            LL  x=c%h;
            for(int  k=last[x];k;k=a[k].next)
            {
                if(a[k].c==c)return  a[k].x;
            }
            return  -1;
        }
}zjj;
LL  ksm(LL  a,LL  b,LL  c)
{
    LL  ans=1%c;a%=c;
    while(b)
    {
        if(b&1)ans=(ans*a)%c;
        a=(a*a)%c;b>>=1;
    }
    return  ans;
}
LL  gcd(LL  a,LL  b){return  (!a?b:gcd(b%a,a));}
LL  solve(LL  a,LL  c,LL  d)
{
    a%=d;c%=d;//这一步也不是很需要，但是可以更远离爆long long
    LL  b=1,cnt=0,tt;
    while((tt=gcd(a,d))!=1)
    {
        if(c==b)return  cnt;//特判
        if(c%tt)return  -1;//无解
        d/=tt;c/=tt;b=(b*a/tt)%d;a%=d;cnt++;
    }
    LL  lim=ceil(sqrt(d*1.0)),now=c;
    for(int  i=0;i<=lim;i++)
    {
        zjj.ins(i,now);
        now=(now*a)%d;
    }
    now=((tt=ksm(a,lim,d))*b)%d/*重复利用*/;
    for(int  i=1;i<=lim;i++)
    {
        int  y=zjj.find(now);
        if(y!=-1)return  i*lim-y+cnt;
        now=(now*tt)%d;
    }
    return  -1;
}
int  main()
{
    LL  a,c,d;
    while(scanf("%lld%lld%lld",&a,&d,&c)!=EOF)
    {
        if(a==0  &&  d==0  &&  c==0)break;
        zjj.clear();
        LL  ans=solve(a,c,d);
        if(ans!=-1)printf("%lld\n",ans);
        else  printf("No Solution\n");
    }
    return  0;
}

线性筛素数

题目描述
【题意】
素数表如下：
2、3、5、7、11、13、17…………
有n次询问，每次问第几个素数是谁？
【输入格式】
第一行n(1<=n<=10000)
下来n行，每行一个整数pi，表示求第pi个素数。1<=pi<=100 0000
【输出格式】
每次询问输出对应的素数。
【样例输入】
3
1
4
7
【样例输出】
2
7
17

线性筛素数有两种，埃式筛和欧拉筛。

埃式筛

我们可以知道，一个数字如果不是质数，那么它的最小质因子一定小于等于这个数字的开平方。

很容易想到，不详细解释。

那么求\(1\)到\(b\)的素数的话，我们可以知道，\(1\)到\(b\)的合数的最小质因数也是一定小于等于\(\sqrt b\)的，那么我们只需要求出\(\sqrt b\)内的所有素数并且暴力for一遍，空间小，复杂度为\(O(n\sqrt n)\)

for(int  i=2;i<=sqrt(b);i++)
{
    if(mp[i]==false)//为素数
    {
        for(int  j=i;j<=b;j+=i)mp[j]=true;
    }
}

给出一种神奇卡常版：

for(register  int  i=3;i<=sqrt(m);i+=2)
{
    if(a[i/2]==true)
    {
        for(register  int  j=i*3;j<=m;j+=i*2)a[j/2]=false;
    }
}

欧拉筛

后面题目主要用欧拉筛，复杂度\(O(nlognlogn)\)

这个就很神奇了，先给出代码：

#include<cstdio>
#include<cstring>
#define  N  21000000
using  namespace  std;
int  ins[2100000];//素数表
bool  mp[N];
int  main()
{
    for(int  i=2;i<=20000000;i++)
    {
        if(!mp[i])ins[++ins[0]]=i;//存入素数表
        for(int  j=1;j<=ins[0]  &&  ins[j]*i<=20000000;j++)
        {
            mp[ins[j]*i]=true;
            if(i%ins[j]==0)break;
        }
    }
    int  n;scanf("%d",&n);
    for(int  i=1;i<=n;i++)
    {
        int  x;scanf("%d",&x);
        printf("%d\n",ins[x]);
    }
    return  0;
}

许多人疑问这一句

if(i%ins[j]==0)break;

如果\(ins_{j}|i\)，那么就可以break了，Why？那么我们设\(i\)为\(d*ins_{j}\)，设\(k>j\)，\(i*ins_{k}=d*ins_{j}*ins_{k}=(d*ins_{k})*ins_{j}\)，我们可以知道\(d*ins_{k}>d*ins_{j}\)，那么在以后的循环，\(i*ins_{k}\)会被重复标记，那么此时就可以break了，一句话就这么精妙。

超级卡常版：

for(register  int  i=3;i<=m;i+=2)
{
    if(a[i/2]==true)b[++k]=i;
    for(register  int  j=1;j<=k  &&  b[j]*i<=m;++j)
    {
        a[b[j]*i/2]=false;
        if(i%b[j]==0)break;
    }
}

当然，慎用卡常版。

欧拉函数

讲解

\(phi(x)\)就是表示在\(1\)~\(x\)与\(x\)互质的数量，叫欧拉函数。

又记作\(φ(x)\)（貌似在前面看到过呢！）

那么我们马上知道\(φ(x)=x-1\)（当\(x\)为质数时）

但是我们又知道几个公式去求呢？

首先，我们做一道题，设\(a*b=y\)，那么在\(1\)到\(y\)，与\(a,b\)互质的数字有多少？（\(a,b\)为质数，且\(a≠b\)）

注意：因为\(a,b\)为质数，且\(a≠b\)，那么\((a,b)=1,[a,b]=a*b\)

那么我们知道\(1-y\)中整除于\(a\)的数量为\(\frac{y}{a}\)，整除于\(b\)的数量为\(\frac{y}{b}\)，整除于\(ab\)的数量为\(\frac{y}{ab}\)，那么\(1-y\)中整除于\(a\)或者整除于\(b\)的数量为\(\frac{y}{a}+\frac{y}{b}-\frac{y}{ab}\)

那么与\(a,b\)互质就是\(y-\frac{y}{a}-\frac{y}{b}+\frac{y}{ab}=y(1-\frac{1}{a}-\frac{1}{b}+\frac{1}{ab})=y(1-\frac{1}{a})(1-\frac{1}{b})\)，那么如果是求\(a^{2}*b=y\)呢？

我们会发现，我们求出了\(a*b\)以内与\(a,b\)互质的数为\(c_{1},c_{2},c_{3}...\)，而\([a,b]\)也就是\(ab\)是整除于\(a\)或\(b\)的，那么\(c_{i}\%(ab)≠0,(ab)\%(ab)==0,(c_{i}+ab)\%ab≠0\)，也就是说\(a^{2}*b\)就是\(a\)个循环的\(a*b\)，也就是说\(phi(a^{2}*b)=y(1-\frac{1}{a})(1-\frac{1}{b})\)。（注意：如果是\(a*b*c\)的话仍然按第一个问题来看，第二个问题是针对素数有次方的情况）

那么我们就得出了\(phi(x)=x*(1-\frac{1}{a1})*(1-\frac{1}{a2})...=(a1^{b1}a2^{b2}a3^{b3}...an^{bn})*\frac{a1-1}{a1}*\frac{a2-1}{a2}...=(a1^{b1-1}(a1-1))(a2^{b2-1}(a2-1))...\)\(=φ(a1^{b1})φ(a1^{b1})...\)（其中的\(m\)表示\(x\)可分解成几个不同的质因数，\(a1,a2,...an\)就是分解出来的不同的质因数，\(bi\)表示的是\(ai\)的次方）

那么我们又可以得出一个公式\(φ(ab)=φ(a)φ(b)\)（\(a,b\)互质），其实这关额证明也很简单，因为他们互质，所以他们所含的质因子不同，那么不会对对方产生任何影响。

当然，不仅仅止步于此，我们设一个质数\(x\)，如何求\(φ(ax)\)？

当\(a\%x≠0\)时，\(a,x\)互质，所以\(φ(ax)=φ(a)φ(x)\)，当\(a\%x=0\)是，\(x\)是\(a\)的其中一个质因数，根据上面可得\(x\)可以合并到\(a\)去得到\(φ(ax)=φ(a)x\)

然后我们发现此过程可以套到欧拉筛里面。

#include<cstdio>
#include<cstring>
#define  N  21000000
using  namespace  std;
int  ins[2100000]/*素数表*/,phi[N]/*欧拉函数*/;
int  main()
{
    for(int  i=2;i<=20000000;i++)
    {
        if(!phi[i])ins[++ins[0]]=i,phi[i]=i-1;//不用mp，直接用欧拉函数的数组判断
        for(int  j=1;j<=ins[0]  &&  ins[j]*i<=20000000;j++)
        {
            if(i%ins[j]==0)//phi(ax)=phi(a)x
            {
                phi[ins[j]*i]=ins[j]*phi[i];
                break;
            }
            else  phi[ins[j]*i]=phi[ins[j]]*phi[i];//phi(ax)=phi(a)phi(x)
        }
    }
    int  n;scanf("%d",&n);
    for(int  i=1;i<=n;i++)
    {
        int  x;scanf("%d",&x);
        printf("%d\n",phi[x]);
    }
    return  0;
}

两道水题

法雷级数

题目描述
【题意】
法雷级数Fi的定义如下：
给定一个i（i>=2），那么所有的 a/b （0<a<b<=i 且 gcd(a,b)==1 ）组成了Fi，
例如： 
F2 = {1/2} 
F3 = {1/3, 1/2, 2/3} 
F4 = {1/4, 1/3, 1/2, 2/3, 3/4} 
F5 = {1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5} 
你的任务就是统计对于给出的i，Fi集合的元素个数。
【输入格式】
第一行n(1<=n<=10000)
下来n行，每行一个整数x，表示求Fx的元素个数。(1<=x<=2000 0000)
【输出格式】
每次询问输出一行一个整数，即Fx的元素个数。
【样例输入】
4
2
3
4
5
【样例输出】
1
3
5
9

我已经不想说什么了，就是求\(2\)到\(x\)的所有\(phi\)函数的值。

#include<cstdio>
#include<cstring>
#define  N  21000000
using  namespace  std;
int  ins[2100000],phi[N];
long  long  sum[N];//要用long long
int  main()
{
    for(int  i=2;i<=20000000;i++)
    {
        if(!phi[i])ins[++ins[0]]=i,phi[i]=i-1;
        for(int  j=1;j<=ins[0]  &&  ins[j]*i<=20000000;j++)
        {
            if(i%ins[j]==0)
            {
                phi[ins[j]*i]=ins[j]*phi[i];
                break;
            }
            else  phi[ins[j]*i]=phi[ins[j]]*phi[i];
        }
        sum[i]=sum[i-1]+phi[i];//sum统计
    }
    int  n;scanf("%d",&n);
    for(int  i=1;i<=n;i++)
    {
        int  x;scanf("%d",&x);
        printf("%lld\n",sum[x]);
    }
    return  0;
}

可见点数

技术图片

【题意】
给出一个正整数N，求在(x,y){0<=x,y<=N}的区域中，
从(0,0)点可以看到的点的个数，
不包括(0,0)自己。
比如上图就是N=5的图，0 ≤ x, y ≤ 5 

【输入格式】
输入有 C (1 ≤ C ≤ 1000) 组数据
每组数据给出一个正整数 N (1 ≤ N ≤ 1000)
【输出格式】
每组数据输出三个整数分别是：第几组，N，和可以看到的点数
【样例输入】
4
2
4
5
231
【样例输出】
1 2 5
2 4 13
3 5 21
4 231 32549

也是水题一道，我们发现沿着对角线切割发现左边的可见点数与右边的可点点数不就是法雷级数吗？

当然，有三个点需要我们特地加上：\((1,1),(1,0),(0,1)\)

那么答案就是\(sum_{i}*2+3\)

#include<cstdio>
#include<cstring>
#define  N  1010
using  namespace  std;
int  ins[2100],phi[N];
long  long  sum[N];
int  main()
{
    for(int  i=2;i<=1000;i++)
    {
        if(!phi[i])ins[++ins[0]]=i,phi[i]=i-1;
        for(int  j=1;j<=ins[0]  &&  ins[j]*i<=1000;j++)
        {
            if(i%ins[j]==0)
            {
                phi[ins[j]*i]=ins[j]*phi[i];
                break;
            }
            else  phi[ins[j]*i]=phi[ins[j]]*phi[i];
        }
        sum[i]=sum[i-1]+phi[i];
    }
    int  n;scanf("%d",&n);
    for(int  i=1;i<=n;i++)
    {
        int  x;scanf("%d",&x);
        printf("%d %d %lld\n",i,x,sum[x]*2+3);
    }
    return  0;
}

原根

当\(a^{x}≡1\mod b\)，满足最小的正整数\(x\)称为\(a\)模\(b\)的阶，很明显\(a,b\)互质才有阶。

原根：当\(a\)模\(b\)的阶等于\(φ(b)\)时，称\(a\)为\(b\)的原根。

我们这里规定原根的数量表示的是\(1\)到\(m\)中为\(m\)原根的数量。

原根有以下性质：

  1. \(a,a^{2},a^{3},a^{4}...,a^{φ(b)}\)在模\(b\)的情况下能不重复的形成\(b\)的所有质因数。（两个集合的数字都有\(φ(b)\)个）
  2. \(a^{kφ(b)}≡1\mod b\)
  3. 一个数字\(m\)有原根的必要条件为\(2,4,p^{n},2p^{n}\)，其中\(p为\)为奇素数，\(n\)为正整数。
  4. 一个数字\(m\)的原根数量\(φ(φ(m))\)

那么如何证呢？

欧拉定理

好，让我们来看看欧拉定理。（雾）

之前跟大家讲了会填坑的

我们知道\(a^{φ(b)}≡1\mod b\)（\(a,b\)不互质），但是这个有什么用？

这个为阶最大为\(φ(b)\)提供了一个必要的条件。

我们来证证吧。

我们设\(b\)的质因子为\(a_{1},a_{2},a_{3}...,a_{φ(b)}\)。

现在有一个\(x\)与\(b\)互质，设\(c_{1}=xa_{1},c_{2}=xa_{2}...\)

  1. 没有一个\(c_{i}≡c_{j}\mod b(i≠j)\)。

这个让我们用反证法证一证吧：

\[c_{i}≡c_{j}\mod b\]

\[c_{i}-c_{j}≡0\mod b\]

\[x(a_{i}-a_{j})≡0\mod b\]

因为\(x\)与\(b\)互质，那么\(a_{i}-a_{j}\)整除于\(b\)，但是\(|a_{i}-a_{j}|＜b\)，所以不成立。

  1. \(c_{i}\)除以\(b\)得到的余数\(u\)与\(b\)互质。

依然用反证法证一证：

\[c_{i}≡u\mod b\]那么\(c_{i}-kb=u\)（\(k\)为未知整数）。

\(b\)和\(k\)不互质，那么\((b,k)>1\)那么我们可以知道原式可化为：\(\frac{a_{i}x}{(b,k)}+\frac{kb}{(a,b)}=\frac{u}{(a,b)}\)

那么后面两个分数都是整数，那\(\frac{a_{i}x}{(b,k)}\)就必须是整数，但是\(a_{i},x\)都与\(b\)互质，所以\(a_{i}x\)就与\((b,k)\)互质，所以不成立。

依据上面我们可以知道\(c\)集合在\(\mod b\)的情况下可以全部不重复映射到\(a\)集合，那么我们将\(c_{1},c_{2},c_{3}...\)乘起来得到\(x^{φ(b)}a_{1}a_{2}a_{3}a_{4}...a_{φ(b)}≡a_{1}a_{2}a_{3}...a_{φ(b)}\mod b\)也就是\((x^{φ(b)}-1)a_{1}a_{2}a_{3}a_{4}...a_{φ(b)}≡0\mod b\)，因为\(a_{1}...\)都与\(b\)互质，所以\(x^{φ(b)}-1≡0\mod b\)，所以\(x^{φ(b)}≡1\mod b\)

证毕。

当然，费马小定理就是欧拉定理的特殊情况，\(b\)为素数时，\(x^{b-1}≡1\mod b\)。

原根部分性质证明（数量证不出来，一个还没填的坑）

注：一下证明中指数都在\(1\)到\(φ(b)\)

如同欧拉定理，我们先证没有一个\(a^{i}≡a^{j}\mod b(i>j)\)

反证法：

假如有\(a^{i}≡a^{j}\mod b(i>j)\)

那么：

\[a^{i}≡a^{j}\mod b\]

\[a^{i}-a^{j}≡0\mod b\]

\[a^{j}(a^{i-j}-1)≡0\mod b\]

那么我们知道\(a\)与\(b\)互质，所以\(a^{j}\)与\(b\)互质，而\(a\)模\(b\)的阶为\(φ(b)\)，\(i-j<φ(b)\)，所以\(a^{i-j}-1≡0\mod b\)不成立，所以\(a^{i}≡a^{j}\mod b(i>j)\)不成立。

再证\(a^{i}\)除以\(b\)得到的余数\(u\)与\(b\)互质。

反证法：

\(a^{i}≡u\mod b\)

\(a^{i}-bk=u\)

然后就跟欧拉定理里面的一样了。

所以我们就证出了\(a,a^{2},a^{3},a^{4}...,a^{φ(b)}\)在模\(b\)的情况下能不重复的形成\(b\)的所有质因数。（两个集合的数字都有\(φ(b)\)个）

\(a^{kφ(b)}≡1\mod b\)

这个怎么证？我们知道\(a^{d}≡1\mod b\)（\(d\)为\(a\)模\(b\)的阶）

那么\(a^{kd}\%b≡(a^{d})^{k}\%b≡1^{j}\%b≡1\)

由于原根的阶就是\(φ(b)\)，所以得证。

当然，数量以及是否有原根我不会证。

听说要群论，我果然还是太菜了。

扩展：原根的求法

这个就很棒了，我们可以先假设\(p\)是奇素数，然后求\(p\)的原根。

以下内容摘自https://oi-wiki.org/math/primitive-root/，OIwiki也十分有名，大家可以上去搜一些OI的东西。

技术图片

当然，我们还会做一些解释，其中这是求\(p\)是奇素数的，当然，可以吧求法中的\(p-1\)换成\(phi(x)\)，其他的也换一下也没有多大问题，依然可以证，不过首先\(p\)要有原根才可以用。

图片中类似\(Vi∈[1,m]：\)的东西表示循环。

这里的裴蜀定理指的是如果有一个二元一次不定式满足：\(ax+by=c\)（\(c|(a,b)\)）那么此不定式就有无数个整数解，当然，在上面同余的时候我们也类似的证了证，那么也就没多大问题了，因为是扩展，就没有代码了QAQ。

代码

题目描述
给出n个正整数，求每个正整数的原根个数。

注意：不是每一个数都有原根！这道题和1159不一样！

输入
第一行一个数n

接下来n行，一行一个数xi。

输出
一行一个数，第i行是xi的原根个数（无原根则输出0）。

样例输入
8
1
2
3
4
8
9
10
18
样例输出
0
1
1
1
0
2
2
2
提示

1<n<=10000


1<=xi<=2*10^7
#include<cstdio>
#include<cstring>
#define  N  21000000
using  namespace  std;
int  ss[2100000],phi[N];
bool  mt[N];
int  main()
{
    mt[2]=mt[4]=true;phi[1]=1;
    for(int  i=2;i<=20000000;i++)
    {
        if(!phi[i])
        {
            phi[i]=i-1,ss[++ss[0]]=i;
            if(i!=2)
            {
                long  long  now=i;
                while(now<=N)//存在原根的地方
                {
                    mt[now]=true;
                    now*=i;
                }
            }
        }
        for(int  j=1;j<=ss[0]  &&  ss[j]*i<=20000000;j++)
        {
            if(i%ss[j])phi[ss[j]*i]=phi[ss[j]]*phi[i];
            else
            {
                phi[ss[j]*i]=phi[i]*ss[j];
                break;
            }
        }
    }
    int  n;scanf("%d",&n);
    for(int  i=1;i<=n;i++)
    {
        int  x;scanf("%d",&x);
        if(mt[x]==true  ||  (x%2==0  &&  mt[x/2]==true))printf("%d\n",phi[phi[x]]);//存在原根
        else  printf("0\n");
    }
    return  0;
}

高斯消元

题目描述
【题意】
有n个未知数x1,x2,x3……xn，满足：
a11*x1+a12*x2+a13*x3……+a1n*xn=b1
a21*x1+a22*x2+a23*x3……+a2n*xn=b2
……………………………………
an1*x1+an2*x2+an3*x3……+ann*xn=bn
求x1,x2,x3……xn的值。（保证有解）
【输入格式】
第一行给出n(1<=n<=100)
下来n行，每行给出n+1个实数，分别是 ai1~ain 和bi。
【输出格式】
输出x1,x2,x3……xn的值（相邻两个用一个空格隔开，每个数保留3位小数）
【样例输入】
3
2.5 5.0 3.0 32.5
1.0 4.5 2.0 22
4.0 3.5 1.5 26.5
【样例输出】
3.000 2.000 5.000

【提示】

aij>0

普通

我们小学做\(n\)元一次方程都是消元的吗，结果没想到OI中叫高斯消元，好像很高大尚。

其实就是用\(1\)式消去\(2\)到\(n\)式的第一项，用\(2\)式消去\(3\)到\(n\)式的第二项...

\(O(n^{3})\)

#include<cstdio>
#include<cstring>
#define  N  110
using  namespace  std;
double  a[N][N],f[N];
int  n;
void  guess()
{
    for(int  i=1;i<=n;i++)
    {
        for(int  j=i+1;j<=n;j++)
        {
            double  bi=a[j][i]/a[i][i];//求出比例
            for(int  k=n+1;k>=i;k--)
            {
                a[j][k]-=a[i][k]*bi;//暴力double减
            }
        }
    }
    for(int  i=n;i>=1;i--)
    {
        double  bi=a[i][n+1];
        for(int  j=i+1;j<=n;j++)bi-=a[i][j]*f[j];
        f[i]=bi/a[i][i];
    }
}
int  main()
{
    scanf("%d",&n);
    for(int  i=1;i<=n;i++)
    {
        for(int  j=0;j<=n;j++)scanf("%lf",&a[i][j+1]);
    }
    guess();
    for(int  i=1;i<n;i++)printf("%.3lf ",f[i]);
    printf("%.3lf\n",f[n]);
    return  0;
}

辗转相除法

辗转相除不是\(gcd\)吗？\(b\%a,a\)呀。

但是在\(guess\)里面，小数有时总是这么不尽任意，虽然有四舍五入，但是整数在调试还是什么方面都很强！

而且如果要求求的是整数解就很棒棒了，所以在矩阵树中的消元许多人宁愿多个\(log\)也要打辗转相除。

复杂度\(O(n^{3}logn)\)

因为没有题目验证正确性，将在矩阵树给出辗转相除版。

先讲讲：

我们用第\(x\)行消掉第\(y(y>x)\)行的第\(x\)项时（根据高斯消元我们知道两行的前\(x-1\)项都已经被消掉了），我们不是暴力直接除，而是将第\(x\)项每一行乘以\(a_{y,x}/a_{x,x}\)减到第\(y\)行，然后交换\(x,y\)行，我们会发现其实就是对\(x\)项做类似辗转相除的操作然后改变一下其他项，当然，为了节省时间也可以不交换，不过得用一些其他方法实现类似交换的操作。

矩阵树与证明

又是一个大的内容。。。

参考资料：

https://www.cnblogs.com/zj75211/p/8039443.html

https://blog.csdn.net/qq_34921856/article/details/79409754

https://www.cnblogs.com/twilight-sx/p/9064208.html

https://blog.csdn.net/a_crazy_czy/article/details/72971868

https://www.cnblogs.com/candy99/p/6420935.html

https://www.cnblogs.com/xzzzh/p/6718926.html

https://baike.baidu.com/item/Binet-Cauchy%E5%AE%9A%E7%90%86/8255247

https://baike.baidu.com/item/%E5%8D%95%E4%BD%8D%E7%9F%A9%E9%98%B5/8540268?fr=aladdin

你看看这么多，就知道这个有多恶心了！！！！！！！！！！！！！！

未了结的坑

矩阵树是解决一个图中生成树的数量。

目前我只会做无向图的，而且也只会证无向图的，当然，按我现在对矩阵树的理解，有没有重边应该也无所谓，大家可以试一试，因为时间紧迫，所以就不证明了，下面的默认没有重边。

因为老师开始要求学几何了，就只能抛坑了QAQ

未填完的坑：

  1. 有向图的矩阵树。
  2. 变元矩阵树。
  3. 证明有重边也无所谓

无向图

关联矩阵

在无向图里面，关联矩阵是\(n*m\)的一个矩阵（\(n\)是点数，\(m\)的边数），如果第\(k\)条无向边是\((i->j)\)，那么矩阵里的\((i,k)\)点值\(++\)，\((j,k)\)的点值\(--\)。（倒过来也可以，无所谓）

给张图更好的理解：

技术图片

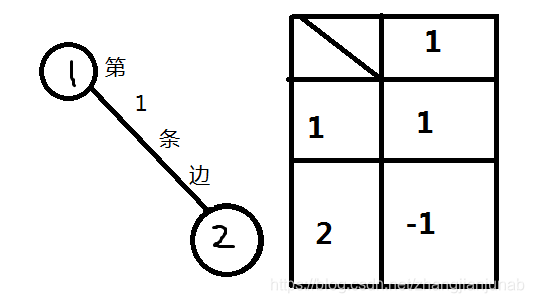
我们设无向图的关联矩阵为\(B\)，\(B\)转置矩阵为\(B^{T}\)

转置矩阵：

就是把现矩阵的第一行作为第一列，第一列作为第一行。

技术图片

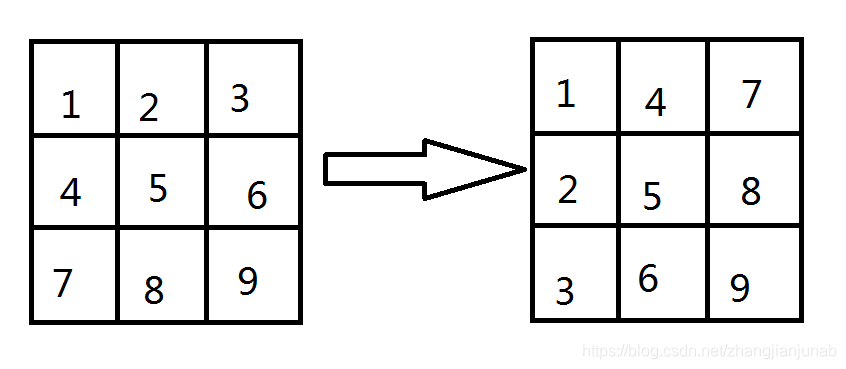
就是转置矩阵。

矩阵乘法：

这里放上度娘的解释https://baike.baidu.com/item/%E7%9F%A9%E9%98%B5%E4%B9%98%E6%B3%95/5446029?fr=aladdin：

技术图片

Kirchhoff矩阵

这里只讲无向图的Kirchhoff矩阵。

Kirchhoff矩阵就是\(BB^{T}\)，也就是一个\(n*n\)的矩阵

\(BB^{T}\)\(_{ij}=\sum_{k=1}^{m}B_{i,k}B^{T}_{k,j}=\sum_{k=1}^{m}B_{i,k}B_{j,k}\)

所以我们可以知道，Kirchhoff矩阵的\((i,j)\)项就是\(B\)的第\(i\)行与第\(j\)行的内积。

当\(i≠j\)时，如果有\(B_{i,k}B_{j,k}=0\)，那么说明第\(k\)条边不是\((i-j)\)的。相反\(B_{i,k}B_{j,k}=-1\)，就代表有一条边，所以我们知道，Kirchhoff矩阵的\((i,j)\)项表示的是\(i-j\)边的个数的相反数，目前只能是\(-1,0\)。

当\(i=j\)时， 如果有\(B_{i,k}B_{i,k}=0\)，那么说明他不在第\(k\)条边上，相反\(B_{i,k}B_{i,k}=1\)就是在，所以Kirchhoff矩阵的\((i,i)\)项表示的是\(i\)的度数。

当然，还有个简单的构建方法，就是（度数矩阵 - 邻接矩阵）。

为什么要将关联矩阵，证明的时候就知了。

我们容易知道这个矩阵的每个行和每个列的和为\(0\)。

因为度数为正，其他数为负，这一行（列）的所有负数的和就是度数的相反数。

行列式

对于一格\(r*r\)的行列式\(A\)：

行列式\(det(A)\)的值为：\(\sum^{r!}_{i=1}(-1)^{k}a_{1,b_{1}}a_{2,b_{2}}a_{3,b_{3}}...a_{r,b_{r}}\)，其中\(a_{ij}\)为\(A\)矩阵的第\(i\)行第\(j\)列。

而\(b_{1},b_{2},b_{3},b_{4}...b_{r}\)是长度为\(r\)的任意一个全排列，然后全排列的个数有\(r!\)，然后\(k\)表示的是\((1,b_{1}),(2,b_{2}),(3,b_{3})...\)的逆序对数（\((i_{1},j_{1}),(i_{2},j_{2})(i_{1}<i_{2},j_{1}>j_{2})\)就是一对逆序对）。

其实就是选\(r\)个点，行和列不重复

比如：

\(2*2\)的矩阵\(O\)

\(\left\{ \begin{matrix} 1 & 2\\ 3 & 4\end{matrix} \right\}\)

\(det(O)=1*4-2*3=-2\)

行列式有一些\(beautiful\)的性质。

定理1：\(A\)与\(A\)的转置矩阵的行列式相等。

我们发现转置后点的相对位置不变，第\(i\)行变成第\(i\)列，第\(j\)列变成了第\(j\)行，本质没变，所以行列式相等。

定理2：当某行（列）的值全部为0，那么这个矩阵的行列式为\(0\)。

怎么选点都有个\(0\)，证毕。

定理3：某一行与某一行交换，行列式取负。

证明：

\((-1)^{k}a_{1,b_{1}}a_{2,b_{2}}a_{3,b_{3}}...a_{r,b_{r}}\)中，现将\(i,j(i<j)\)行互换。

设从\(i+1\)到\(j-1\)，有\(q_{1}\)个数字的\(b\)（也就是列数）小于\(b_{i}\)，有\(q_{2}\)个大于\(b_{i}\)，有\(p_{1}\)个数字小于\(b_{j}\)，有\(p_{2}\)个大于\(b_{j}\)，\(N=(j-1)-(i+1)+1=j-i+1\)，不可能有相等的。

那么交换前\(b_{i},b_{j}\)的贡献有\(q_{1}+p_{2}\)对，交换后有\(q_{2}+p_{1}\)

那么两个相减为：\(q_{1}+p_{2}-q_{2}-p_{1}=q_{1}+p_{2}-(N-q_{1})-(N-p_{2})=2q_{1}+2p_{2}-2N=2(q_{1}+p_{2}-N)\)，而却\(b_{i}\)与\(b_{j}\)交换的又会加\(1\)或减\(1\)，所以取反。

交换列其实也是一样的。

定理4：有两行（列）相等，行列式值为\(0\)

交换两列后的行列式取反，但是我们发现两次的行列式是相等的，所以\(-x=x\)，\(x=0\)，行列式的值为\(0\)。

定理5：当有一行有公因子时，可以把公因子提出（相反，外面有个系数，乘到里面某一行（列）也是可以的）。

定理6：当一行（列）为另一行（列）的比例时，行列式的值为\(0\)。

将这一行的因子提出，和另一行相等，行列式的值为\(0\)。

定理7：某一行（列）的数字依次加上一些数字，那么加上后的行列式可以拆为两个行列式相加：

如：矩阵\(A\)为\(\left\{ \begin{matrix} a_{1,1} & a_{1,2}\\ a_{2,1} & a_{2,2}\end{matrix} \right\}\)，\(B\)为\(\left\{ \begin{matrix} a_{1,1} & a_{1,2}\\ a_{2,1}+c_{1} & a_{2,2}+c_{2}\end{matrix} \right\}\)，\(C\)为\(\left\{ \begin{matrix} a_{1,1} & a_{1,2}\\ c_{1} & c_{2}\end{matrix} \right\}\)，那么\(det(B)=det(A)+det(C)\)

其实很简单证，原本每个式子为：\((-1)^{k}a_{1,b_{1}}a_{2,b_{2}}a_{3,b_{3}}...a_{r,b_{r}}\)，现在为\((-1)^{k}a_{1,b_{1}}a_{2,b_{2}}a_{3,b_{3}}...,(a_{i,b_{i}}+c_{i}),a_{(i+1),b_{i+1}}...,a_{r,b_{r}}\)根据乘法分配率，这是可以拆开的。

定理8：某一行加上另为一行的倍数，行列式的值不变。

很简单，现在的行列式拆成原来的和某个奇怪的，某个奇怪的行列式存在一行是另一行的比例关系，所以这个行列式为\(0\)，不影响值。

通过定理8，我们发现可以对行列式进行消元，类似高斯消元一样，消成类似\(\left\{ \begin{matrix} a_{1,1}' & a_{1,2}' & a_{1,3}'\\ 0 & a_{2,2}' & a_{2,3}'\\ 0 & 0 & a_{3,3}'\\\end{matrix} \right\}\)的样子

我们管这个矩阵叫上三角矩阵，很明显，行列式的值就是对角线的值。

求法

其实生成树的个数就是Kirchhoff矩阵的\(n-1\)阶代数余子式的行列式值结果。

一个矩阵（长宽相等）的\(n-1\)阶余子式删去第\(i\)行与第\(j\)列。

假设我们又乘上了\((-1)^{{1+2+3+...+n-i}+(1+2+3+...+n-j)}\)

就是\(n-1\)阶的代数余子式，我们可以化简一下：\((-1)^{{1+2+3+...+n-i}+(1+2+3+...+n-j)}=(-1)^{n(n-1)-i-j}=(-1)^{-i-j}=(-1)^{i+j}\)

Kirchhoff矩阵对于行列式又有一些性质：

定理1：Kirchhoff矩阵的两个不同的\(n-1\)阶代数余子式的行列式相等。

我们设两个余子式删的行是同一行，不同列（可以类似的推出不同行，同列，然后得证）

两个矩阵为\(C_{i,j},C_{i,k}(j<k)\)（删去第\(i\)行，第\(j\)或\(k\)列）。

我们先将原本的矩阵变换一下，第\(j\)列取反，然后加去除\(j,k\)列的其他列乘上\(-1\)的值，因为每一行的值为\(0\)，那么第\(j\)列的数字就等于\(0\)减去除\(k\)列的其他所有数字，也就是第\(k\)列的数字，然后我们将这一列在\(C_{i,k}\)中一直移到\(k-1\)列（也就是\(C_{i,j}\)中\(k\)列的位置），要交换\(k-j-1\)次，那么这个交换过程就乘上\((-1)^{k-j}\)次，然后\((-1)^{k-j}*(-1)^{i+k}=(-1)^{j-k}*(-1)^{i+k}=(-1)^{i+j}\)，所以我们就将\(C_{i,k}\)转换成\(C_{i,j}\)，且并没改变值，得证。

定理2：Kirchhoff矩阵的行列式的值为\(0\)。

\(Why?\)

因为每一行的和为0，在形成上三角的过程中，最后一行消掉和\(n-1\)个\(0\)，，但是最后一行的和为\(0\)，所以\(n\)个都是\(0\)。

代码

我们默认去掉第\(n\)行第\(n\)列。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#define  N  30
using  namespace  std;
typedef  long  long  LL;
double  a[N][N],hehe=1e-8/*精度交换*/;
int  n,m;
void  zwap(double  &x,double  &y){double  z=x;x=y;y=z;}
double  guess()
{
    for(int  i=1;i<=n;i++)
    {
        int  what=i;//前i-1列不能交换
        while(fabs(a[what][i])<=hehe)what++;
        if(i==n+1)return  0;//没办法
        for(int  j=1;j<=n;j++)zwap(a[what][j],a[i][j]);
        for(int  j=i+1;j<=n;j++)
        {
            double  bi=a[j][i]/a[i][i];
            for(int  k=n+1;k>=i;k--)a[j][k]-=a[i][k]*bi;
        }
    }
    double  ans=a[1][1];
    for(int  i=2;i<=n;i++)ans=ans*a[i][i];
    return  fabs(ans);
}
int  main()
{
    scanf("%d%d",&n,&m);n--;
    for(int  i=1;i<=m;i++)
    {
        int  x,y;scanf("%d%d",&x,&y);
        a[x][x]+=1;a[y][y]+=1;
        a[x][y]-=1;a[y][x]-=1;
    }
    printf("%.0lf",guess());
    return  0;
}

辗转相除法：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#define  N  30
using  namespace  std;
typedef  long  long  LL;
LL  a[N][N];
int  n,m;
void  zwap1(int  &x,int  &y){int  z=x;x=y;y=z;}
void  zwap2(LL  &x,LL  &y){LL  z=x;x=y;y=z;}
LL  guess()
{
    int  now,cnt;
    for(int  i=1;i<=n;i++)
    {
        int  what=i;
        while(a[what][i]==0)what++;
        if(i==n+1)return  0;
        for(int  j=1;j<=n;j++)zwap2(a[what][j],a[i][j]);
        for(int  j=i+1;j<=n;j++)
        {
            now=i,cnt=j;//传说中免交换神器 
            while(a[now][i])
            {
                LL  bi=a[cnt][i]/a[now][i];//辗转相处 
                for(int  k=i;k<=n;k++)a[cnt][k]-=a[now][k]*bi;
                zwap1(now,cnt);
            }
            if(cnt!=i)for(int  k=i;k<=n;k++)zwap2(a[j][k],a[i][k]);//交换 
        }
    }
    LL  ans=a[1][1];
    for(int  i=2;i<=n;i++)ans=ans*a[i][i];
    return  abs(ans);
}
int  main()
{
    scanf("%d%d",&n,&m);n--;
    for(int  i=1;i<=m;i++)
    {
        int  x,y;scanf("%d%d",&x,&y);
        a[x][x]++;a[y][y]++;
        a[x][y]--;a[y][x]--;
    }
    printf("%lld\n",guess());
    return  0;
}

证明

根据柯西-比内公式（后面会有比较垃圾的证明）可得：

\(det(B'B'^{T})=\sum_{U∈S}^{|S|}det(B'_{U})det(B'^{T}_{U})=\sum_{U∈S}^{|S|}(det(B'_{U}))^{2}\)

\(B'\)表示的是，\(U\)代表在\(m\)中随便选\(n-1\)个不重复数字的集合，\(S\)表示所有\(U\)的集合，\(B'_{U}\)就是\(n-1\)行选\(n-1\)列的一个\((n-1)*(n-1)\)的集合，\(B'^{T}_{U}\)选\(n-1\)列，那么我们会发现选\(n-1\)行不就是找到\(n-1\)条边？

讨论情况：

  1. 如果有几条边构成一个环，那么这个\(det\)为\(0\)。

我们一步步把这几行几列换到一起，组成一个类似\(\left\{ \begin{matrix} 1 & 0 & 1\\ -1 & 1 & 0\\ 0 & -1 & -1\\\end{matrix} \right\}\)的小矩阵，因为每条边都只有两个数字，所以这\(3\)列这个行列式的这\(3\)列只能在这一选一个数字来乘，所以我们可以认为这个矩阵的行列式等于这个矩阵去掉这三列的行列式乘以这个小矩阵的行列式，正负先不管，大家可以画个图模拟一下，因为这三行这三列只能在这个小矩阵里面选。

但是这个小矩阵我们消列，变成下三角，\(\left\{ \begin{matrix} a & 0 & ... & ±a\\ -a & ±a & ... & 0\\ ... & ... & ... &...\\ 0 & ...& ±a & ±a\end{matrix} \right\}\)（\(a=±1\)），我们发现先用第一列消最后一列，最后一列第二个又有数字，就用第二列消，也就是依次用第一列一直下去消，那么我们模拟一下过程，当第一行消最后一列时，用\(a\)消\(a\)时，最后一列加上第一列的取反，那么最后一列第二个元素为\(a\)，如果用\(a\)消\(-a\)，直接加，那么最后一列的第二个数字等于\(-a\)，怎么这么巧，消完后最后一列的第二个元素就等于第一个？其实仔细想想就知道，就是是从第二列开始去消也是，那么最终会右下角的倒数两行两列就变成了\(\left\{ \begin{matrix} b & c \\ -b & -c\end{matrix} \right\}(b=±1,c=±1)\)，那么最后一列就是倒数第二列的\(±1\)倍，行列式的值为\(0\)。

  1. 没有环为\(±1\)

我们已经把第\(n\)行消掉，又没有环，必然有一条边是连向\(n\)的，那么我们这一列选的就是这条边的另外一个端点，但是\(n\)个点的图\(n-1\)边不就是棵树吗，而且一边占一列，我们可以认为一条边选一个点且选的点不重复，那么就是在\(n-1\)列里面选\(n-1\)个点。

我们会发现这个端点就是另外一些边的端点，那么这些边又只能选另外一个端点，以此类推，这个行列式的有效选点只有一种，所以为\(±1\)，再取个平方就是\(1\)

通过上面我们会发现Kirchhoff矩阵的\(n-1\)阶代数余子式的行列式值就是生成树的个数！

柯西-比内公式

我是看度娘证明的，很不错https://baike.baidu.com/item/Binet-Cauchy%E5%AE%9A%E7%90%86/8255247。

当然，参考链接有，里面提到的Laplace展开定理我也不会，但是其中用到Laplace展开定理的地方我们都可以感性的理解。。。

我就是对它的一个补充说明

提一下，就是柯西比内公式讲了

技术图片

放上图片，然后一一解释：

技术图片

一个\(4*4\)的单位矩阵为\(\left\{ \begin{matrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{matrix} \right\}\)，也就是对角线为\(1\)，单位矩阵乘以任何矩阵都等于矩阵本身。

我们把M的第n+1,n+2......n+s行的第技术图片 倍加到第k行去.(k=1,2......n)，也就是用\((A*(-I))+A\)将\(A\)的位置全部变为0，然后原本\(0\)的位置加上\(AB\)变成了\(C\)，并且行列式的值并没变。

下面的证明不理\(-1\)先

因为前面的\(n\)行只能选\(C\)中的数字，且\(C\)为\(n*n\)，\(B\)为\(s*n\)，所以\(B\)里面的数字也不能选，只能选\(-I(s*s)\)里面的数字。

那么\(det(N)=det(C)*det(-I)=det(AB)*det(-I)\)

\(det(M)=det(N)=det(AB)*det(-I)\)

对\(M\)进行分解，前\(n\)行只能选\(A\)中的数字，当\(n>s\)时，选\(n\)行必定有些选不到\(A\)里面选到了\(0\)，所以为\(0\)，如果\(n=s\)，那么就是只能选\(A、B\)里面的数字了，也就是\(det(C)=det(AB)=det(A)*det(B)\)，但是\(n>s\)时，我们就只能选\(n\)列，那么我们可以相应的知道\(-I\)中只能选主对角线上（从左上到右下的对角线）的\(s-n\)点，也就是\(i-n=j\)（类似行等于列），那么\(B\)也就只能选其他行的\(n\)个点，那么也就是我们选\(A\)的那些列的列数，也就得到了我们柯西-比内的基本结构了，但是我们并没有理正负。

当\(n≥s\)时

\(det(C)*det(-I)\)的正负数：

\(det(-I)=(-1)^{s}\)，而且\(-I\)中的\(s\)个点每个点都与\(C\)中的\(n\)个点组成逆序对数，也就是\(ns\)，所以\(det(C)*det(-I)\)在理正负的情况下为\(det(C)*(-1)^{(n+1)s}\)。

\(det(M)\)分解后（因为那个公式实在太难写了QAQ）的正负号：

\(A\)与\(B\)的数字构不成逆序对数，那么我们考虑\(-I\)的，我们设选的\(A\)的列数为\(d_{1},d_{2},...,d_{n}\)，那么\(B\)选的行数就为\(d_{1}+n,d_{2}+n,...,d_{n}+n\)

我们设现在选的其中一个\(-I\)主对角线的点的行列为\(i,j\)，那么再看我们在\(A,B\)选的\(2n\)个点，\(A\)中的点的行数皆小于\(i\)，当\(d_{k}>j\)时（\(1≤k≤n\)）有逆序对，\(B\)中的点列数皆小于\(j\)，当\(d_{i}+n<i\)时有逆序对，拆开为\(d_{i}+n<j+n,d_{i}<j\)，发现当\(d_{i}<j\)和\(d_{i}>j\)都有一个逆序对，那么\(-I\)中每个点都有\(n\)个逆序对，也就是\(n(s-n)\)个，\(-I\)自带\(s-n\)个\(-1\)，那么就是\((-1)^{(n+1)(s-n)}\)

证明\((n+1)s=(n+1)(s-n)\)的奇偶性相等。

当\(n\)为奇数，得证QMQ。

当\(n\)为偶数，\(s\)为奇数偶数时，\(s\)与\(s-n\)的奇偶都是一样的。

那么也就是相等，所以柯西-比内公式得证。

不会Laplace展开定理就是烦QAQ。

小结

还是好多坑没填QAQ。

各种友(e)善(xin)数论总集（未完待续），从入门到绝望

标签：方程组   solution   裴蜀定理   位置   +=   problem   sizeof   href   \n   

原文地址：https://www.cnblogs.com/zhangjianjunab/p/10847887.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！