7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0
8 4000
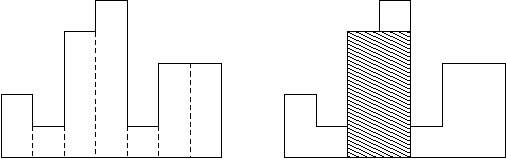
给你一个直方图,告诉你各个条形矩形的高度,求基线对齐构成的矩形中面积最大的矩形的面积对于每一个矩形。面积 = h[i]*(j-k+1),其中j,k是左右边界,h[i]是矩形的高。并且对于j <= x <= k,h[i] <= h[x]。
我们只需要求出每条矩形最多可以向两边拓展的宽度,就可以算出以这个矩形高度为高的最大子矩形面积。最后我们求一个最大值即可。
笛卡尔树的树根是这一子树中键值最小(或最大)的元素;且对于某个序列的笛卡尔树,其任一子树的中序遍历恰好是对应了原序列中的一段连续区间。
我们会发现笛卡尔树同时满足二叉树搜索和堆的性质:
A Cartesian tree may be constructed in linear time from its input sequence. One method is to simply process the sequence values in left-to-right order, maintaining the Cartesian tree of the nodes processed so far, in a structure that allows both upwards and downwards traversal of the tree. To process each new value x, start at the node representing the value prior to x in the sequence and follow the path from this node to the root of the tree until finding a value y smaller than x. This node y is the parent of x, and the previous right child of y becomes the new left child of x. The total time for this procedure is linear, because the time spent searching for the parent y of each new node x can be charged against the number of nodes that are removed from the rightmost path in the tree.
An alternative linear-time construction algorithm is based on the all nearest smaller values problem. In the input sequence, one may define the left neighbor of a value x to be the value that occurs prior to x, is smaller than x, and is closer in position to x than any other smaller value. The right neighbor is defined symmetrically. The sequence of left neighbors may be found by an algorithm that maintains a stack containing a subsequence of the input. For each new sequence value x, the stack is popped until it is empty or its top element is smaller than x, and then x is pushed onto the stack. The left neighbor of x is the top element at the time x is pushed. The right neighbors may be found by applying the same stack algorithm to the reverse of the sequence. The parent of x in the Cartesian tree is either the left neighbor of x or the right neighbor of x, whichever exists and has a larger value. The left and right neighbors may also be constructed efficiently by parallel algorithms, so this formulation may be used to develop efficient parallel algorithms for Cartesian tree construction.
Another linear-time algorithm for Cartesian tree construction is based on divide-and-conquer. In particular, the algorithm recursively constructs the tree on each half of the input, and then merging the two trees by taking the right spine of the left tree and left spine of the right tree and performing a standard merging operation. The algorithm is also parallelizable since on each level of recursion, each of the two sub-problems can be computed in parallel, and the merging operation can be efficiently parallelized as well.
比较常用的是第一种构造方式。仔细思考即可理解。
对于这道题而言,建出小根堆笛卡尔树后,\(ans=\max\{h[i]*siz[i]\}\)。 时间复杂度\(O(n)\)
#include<iostream>
#include<algorithm>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0;rg char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-') data=-data;
for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
return data;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;
co int N=1e5+1;
int n,h[N];
int st[N],top;
int lc[N],rc[N],siz[N];
ll ans;
void dfs(int x){
siz[x]=1;
if(lc[x]) dfs(lc[x]),siz[x]+=siz[lc[x]];
if(rc[x]) dfs(rc[x]),siz[x]+=siz[rc[x]];
ans=max(ans,(ll)h[x]*siz[x]);
}
void Largest_Rectangle_in_a_Histogram(){
top=0,fill(lc+1,lc+n+1,0),fill(rc+1,rc+n+1,0);
for(int i=1;i<=n;++i){
read(h[i]);
for(;top&&h[st[top]]>h[i];--top) lc[i]=st[top];
rc[st[top]]=i,st[++top]=i;
}
ans=0,dfs(st[1]);
printf("%lld\n",ans);
}
int main(){
while(read(n)) Largest_Rectangle_in_a_Histogram();
return 0;
}HDU1506 Largest Rectangle in a Histogram
标签:bsp size others 技术 root key 对齐 tac compute
原文地址:https://www.cnblogs.com/autoint/p/10843830.html