标签:新手 计算 情况 说明 是什么 mic 网络流 利用 破坏
先来理解几个概念
在原先能够流通的网络中移除的边集,使得网络无法流通
所有的割中边权和最小的割即为最小割
可以想象一下,Kido为了自给自足给自己建了超多供水管道(kido能进行光合作用),形成了一个网络,然后容量越大的管道防护设施越好,但是总有人想渴死Kido就想炸掉管道,但是贫乏的恐怖分子既想渴死kido又想节约成本,那么最节约成本的破坏管道的方案即为最小割
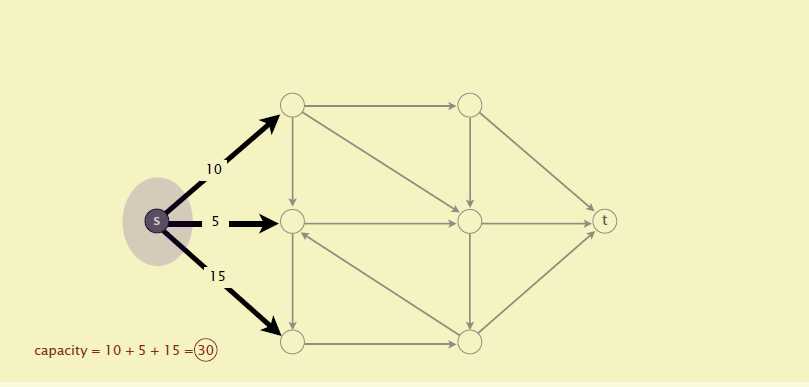
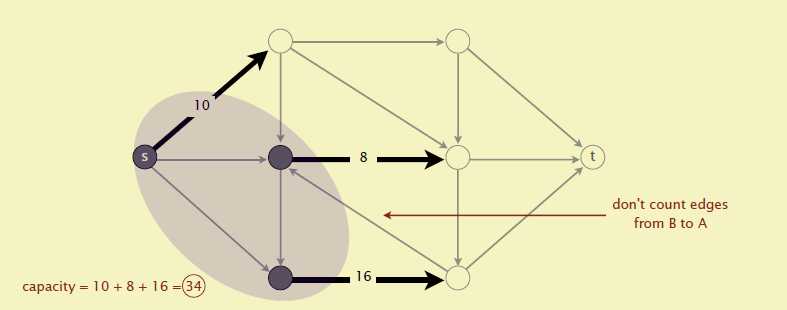
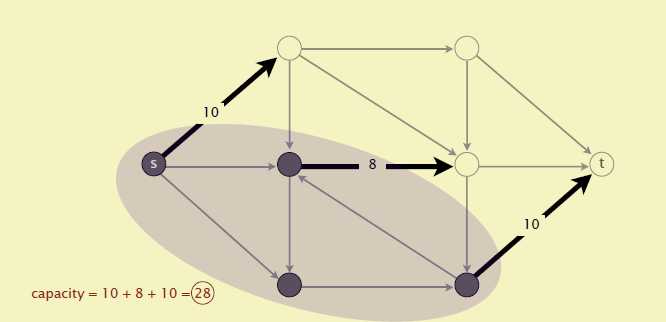
在任何的网络中,最大流的值等于最小割的容量
要证明上面的定理,只要证明下面三个条件是等价的就可以了:
(1)存在一个割的容量等于flow f的值
(2)f是最大流
(3)对于f没有增广路径
首先我们证明(1)->(2)。假设我们有一个割(A,B)的容量等于f的值,那么利用弱对偶的关系,其他流的值<=(A,B)的容量,而由于1的假设,(A,B)的容量等于f的值,因此得到其他流的值都小于f的值,从而(2)成立
接着证明(2)->(3)。我们来证明它的逆否命题。对于f如果还有还有增广路径,那f不是最大流,这很显然,如果按照FF算法的话,我们还可以增加flow f的值,因此f就不会是最大流,因此逆否命题成立,也就代表(2)->(3)成立。
最后证明从(3)->(1)。让割(A,B)满足这么一个条件:s在A中,且A中的顶点通过一些无向的边连接而成,这些边要么是不是满的前向边要么是非空的反向边。如下图中加粗的边。
那么根据定义,s在A中,由于没有增广路径,因此t在B中。
由于这个割的B到A的边流量全是0,
这个割的容量 = 沿着这个割的netflow(从A到B边的流量-从B到A边的流量)
又根据flow-value引理,netflow = value of low,因此推出(1).
最近在看maxflow相关的资料,本文主要介绍下自己对最大流和最小割的理解。最大流本来是网络流方面的算法,后来在计算机视觉中也得到广泛的应用,如图割。我觉得要理解一个算法首先要从起源开始,然后再去泛化问题、建立模型,最后才是解决之。本文是以一个新手的角度去理解算法。
首先从最简单的开始,先看一幅图: 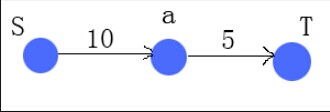
有3个节点S,a,T,边[S,a]的容量是10,边[a,T]的容量是5,假设从S处要传送数据到T,问最大传送数据量是多少?应该是min(10,5)=5.如果超出5,[a,T]边容不下,因此传不过去,此时的最大流量就是5,[a,T]边就是该图的一条最大流。该图可以想象成从S到T通水,需要修建水管,a是中间站点,S到a修建的水管可以容纳下10单位的水量,a到T可容下5单位的水量,现在有个人不想让S到T通水了,那么他得要切割水管,那么应该切割哪条水管呢?假设切割水管付出的代价和水管容量成正比。显然,他需要切割a到T的水管,而不会切割S到a的水管,此时的割是最小割,容量是5,最大流是5,所以最大流=最小割。当然这个例子太简单,不能说明普遍问题。
来个稍微复杂的例子: 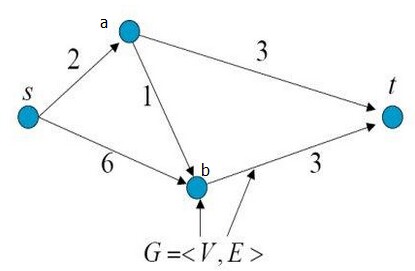
从S到T,中间经过a,b两节点,问此时的最大流是多少?
首先找一条从S到T的路径[S,a,t],该路径的最大流量是min(2,3)=2,因为[S,a]上面的容量已经被用了,所以路径[S,a,b,t]就行不通了,割去[S,a]后图变成了以下形式: 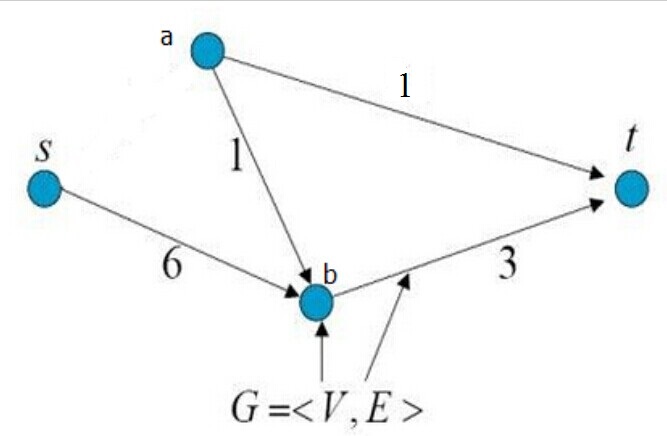
该图叫做残留网络或者叫残留图,此时再找从S到t的路径[S,b,t],路径的最大流量是min(3,6)=3.割去[b,t]后,图如下: 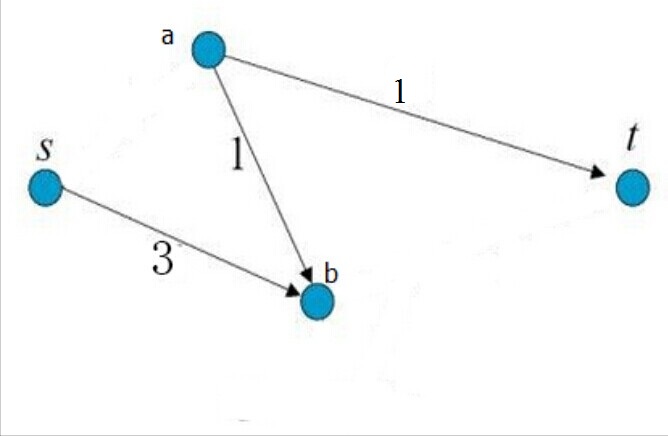
此时就不存在从S到t的可行路径了,则结束最大流的查找。此时的最大流是2+3=5,被割的边容量和是2+3=5,即最大流=最小割。
两个例子我们已经能理解最大流和最小割大体的含义了,也发现最大流的确和最小割是相等的。只从这两个小例子就证明最大流和最小割相等是绝对不严格的,严格的数学证明可google相关资料。回头思考下,最大流到底是什么?如果以送货为例,在可行的情况下,从一个节点到另一个节点所能送达的最大货量即为最大流。打个比方,假设从S处开始放弹珠,让其自动滚到t处,箭头方向为下坡路,在不考虑时间和空间(即把弹珠想象成质点)的情况下,路径中能容纳的最大弹珠量即为最大流量,最小割就是把容纳的弹珠量和容量相同的边都割去,得到的割即为最小割,显然最大流=最小割,因为最大流量完全由路径和容量决定。割去这些边之后,弹珠是没法从S滚落到t的。
标签:新手 计算 情况 说明 是什么 mic 网络流 利用 破坏
原文地址:https://www.cnblogs.com/graytido/p/10849560.html