关于判断可图、图单连通性几题

标签：style   blog   class   code   c   tar   

1、输入一个图的度数列判断是否可图。

      省赛原题。   SX数据。 (现在想想那个一A真是莫明其妙，不过卡了后面的题也算是败了RP吧。)

      原题链接在此：http://acm.hdu.edu.cn/showproblem.php?pid=2454

      未名湖一题在此：http://poj.org/problem?id=1659  

      以上两题用HH(判断可图的)贪心都可以过，复杂度要求不是很高。

      Erd?s–Gallai theorem  链接：http://en.wikipedia.org/wiki/Erd%C5%91s%E2%80%93Gallai_theorem

   A sequence of non-negative integers 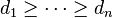 can be represented as the degree sequence of a finite simple         graph on n vertices if and only if 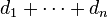 is even and

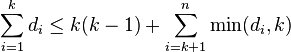
   holds for .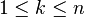

      orz xl大牛

      附个O(n*log(n))的代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int maxn = 1e5+1;
int N, a[maxn];
LL s[maxn];
inline void init() {
    memset(s, 0, sizeof(s));
}
int main()
{
    int T;
    scanf("%d", &T);
    while(T--){
        scanf("%d", &N); {
            init();
            for (int i=1; i<=N; ++i) {
                scanf ("%d", &a[i]);
                a[i] = -a[i];
            }
            sort(a+1, a+N+1);
            for (int i=1; i<=N; ++i) {
                s[i] = s[i-1]-a[i];
            }
            if (s[N]%2==1) {
                printf ("no\n");
                continue;
            }
            bool flag = true;
            for (int r=1; r<=N; ++r) {
                int pos = upper_bound(a+r+1, a+N+1, -r)-a;
                if (s[r]> 1LL*r*(r-1)+  s[N]-s[pos-1]+  1LL*r*(pos-r-1)) {
                    flag = false;
                    break;
                }
            }
            printf ("%s\n", flag ? "yes" : "no");
        }
    }
    return 0;
}

2、判单连通。

    原题在此： http://poj.org/problem?id=2186

    简单思路：缩点后，能有一条链经过所有的强连通分量。

    ps:图论真是很巧妙又很开阔思维的，YY一条链...

    图论继续搞起。

   admin那个并查集思路果断AC不了数据强的题。。。

    标程真是奇葩。

    不附代码了，网上好多。

关于判断可图、图单连通性几题,布布扣,bubuko.com

关于判断可图、图单连通性几题

标签：style   blog   class   code   c   tar   

原文地址：http://blog.csdn.net/cgf1993/article/details/25817693