标签:导数 梯度下降 决策 最大的 正则 简单 上进 拆分 能力
给定由$d$个属性描述的示例$x=(x_{1};x_{2};...;x_{d})$,其中$x_{i}$是$x$在第$i$个属性上的取值,线性模型学习一个属性的线性组合来预测函数,即$$f(x)=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}+b(3.1)$$一般写成向量形式$$f(x)=w^{T}x+b(3.2)$$其中$w=(w_{1};w_{2};...;w_{d})$。$w$和$b$学得之后,模型(函数)就确定了。
下面介绍几种经典线性模型,包括回归、二分类和多分类。
给定数据集$D=\left \{ (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m}) \right \}$,其中$x_{i}=(x_{i1};x_{i2};...;x_{id})$,$y_{i}\in \mathbb{R}$。“线性回归”试图学习一个线性模型能够尽可能拟合给定的数据。
先考虑输入样本只有一个属性的情况。可以表示为$D=\left \{ (x_{i},y_{i}) \right \}_{i=1}^{m}$,其中$x_{i}\in \mathbb{R}$。对于离散属性,若属性之间存在“序关系”,比如“大中小”三个属性显然不能随意分配值,应按“大中小”或“小中大”顺序分配赋值,可以转化为连续值,例如二值属性“高”和“矮”可转化为{1.0,0.0};若属性之间不存在“序关系”,假如有$k$个属性值,可以转化为$k$维向量,比如“西瓜”、“南瓜”和“冬瓜”,可以转化为(0,0,1)、(0,1,0)和(1,0,0)(这是one-hot表示)。
线性回归学得$$f(x_{i})=wx_{i}+b,使得f(x_{i})\approx y_{i}(3.3)$$如何求得$w和b$,关键在于衡量$f(x)$和$y$之间的差别,我们可以使用均方误差衡量,计算所有样本的真实值和预测值之间的差距,再将所有差距求和,再求极小化值即可得。即$$(w^{*},b^{*})=\underset{(w,b)}{argmin}\sum_{i=1}^{m}(f(x_{i})-y_{i})^2$$$$=\underset{(w,b)}{argmin}\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^2(3.4)$$均方误差对应了欧氏距离,基于均方误差最小化来进行求解方程的方法称为“最小二乘法”,线性回归就是通过“最小二乘法”找到一条直线,使得所有点到这条直线的欧氏距离之和最短。
求解$w和b$使得$E_{(w,b)}=\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^2$最小化的过程称为线性回归模型最小二乘的“参数估计”,也就是估计参数。直接对$w$和$b$求导可得$$\frac{\partial E_{(w,b)}}{\partial w}=2(w\sum_{i=1}^{m}x_{i}^{2}-\sum_{i=1}^{m}(y_{i}-b)x_{i})(3.5)$$$$\frac{\partial E_{(w,b)}}{\partial b}=2(mb-\sum_{i=1}^{m}(y_{i}-wx_{i}))(3.6)$$令上述两式为0得$w$和$b$最优闭式解$$w=\frac{\sum_{i=1}^{m}y_{i}(x_{i}-\overline{x})}{\sum_{i=1}^{m}x_{i}^{2}-\frac{1}{m}(\sum_{i=1}^{m}x_{i})^2}(3.7)$$$$b=\frac{1}{m}\sum_{i=1}^{m}(y_{i}-wx_{i})(3.8)$$
更一般的情形是数据集为$D$,样本由$d$个属性描述,此时可学得“多元线性回归”。类似的可利用最小二乘法对$w$和$b$进行参数估计。为方便,把$w$和$b$吸入向量形式$\hat{w}=(w;b)$,相应的把数据集$D$表示为一个$m\times (d+1)$大小的矩阵$X$,其中每行对应一个示例,该行前$d$个元素对应示例$d$个属性值,最后一个恒为1(因为1和$b$相乘还是$b$),即
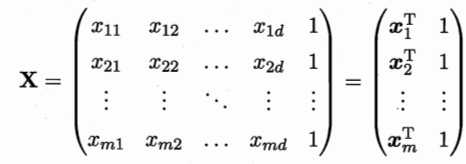
把标记也写成向量形式$y=(y_{1};y_{2};...;y_{m})$,则有$$\hat{w}^{*}=\underset{\hat{w}}{argmin}(y-X\hat{w})^{T}(y-X\hat{w})(3.9)$$令$E_{\hat{w}}=(y-X\hat{w})^{T}(y-X\hat{w})$,对$\hat{w}$求导可得$$\frac{\partial E_{\hat{w}}}{\partial \hat{w}}=2X^{T}(X\hat{w}-y)(3.10)$$令上式为0可得$\hat{w}$最优解的闭式解,因为涉及矩阵逆运算,需要讨论。当$X^{T}X$为满秩矩阵或正定矩阵时,可轻松得到$$\hat{w}^{*}=(X^{T}X)^{-1}X^{T}y(3.11)$$令$\hat{x}_{i}=(x_{i};1)$,最终学得的多元线性回归模型为$$f(\hat{x}_{i})=\hat{x}_{i}^{T}(X^{T}X)^{-1}X^{T}y(3.12)$$然而,现实中$X^{T}X$往往不是满秩矩阵,例如样本特征太多,维数超过了样本数量,导致$X$列数多于行数,$X^{T}X$显然不满秩,此时可以解出多个解,选择哪个解输出是由算法的偏好决定的,常见的做法是引入正则化项(解决过拟合)。
线性回归模型有许多变种,我们将最简单的形式写为$$y=w^{T}x+b(3.13)$$例如标记$y$的对数作为线性模型可得$$lny=w^{T}x+b(3.14)$$这就是“对数线性回归”,实际上它试图让$e^{w^{T}x+b}$逼近$y$。式(3.14)形式上还是线性回归,但实质是求输入到输出的非线性映射。
更一般地,考虑单调可微函数$g(\cdot )$,令$$y=g^{-1}(w^{T}x+b)(3.15)$$这样模型称为“广义线性模型”,其中$g(\cdot )$称为“联系函数”。
上面都是关于回归任务的形式,但若是做分类任务呢?可以通过(3.15)广义线性模型,只需找到一个可微函数将分类任务真实标记$y$与线性回归模型预测联系起来即可。考虑二分类,输出为$y\in \left \{ 0,1 \right \}$,线性回归产生预测值是$\mathbb{R}$,可以将此时的实数转换为0/1值。最简单的是“单位阶跃函数”$$y=\begin{cases}0, & \text{ } z<0; \\ 0.5, & \text{ } z=0; \\ 1, & \text{ } z>0. \end{cases}(3.16)$$形象化可如下图所示
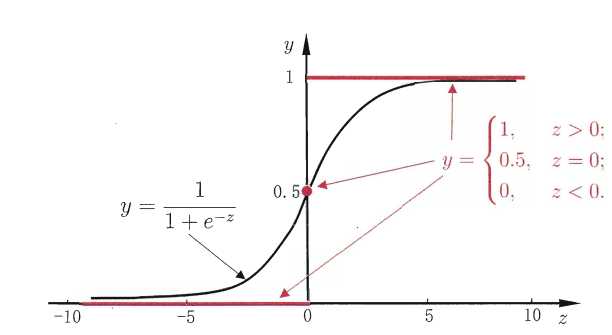
上述单位阶跃函数不连续,不能用作$g^{-}(\cdot )$,希望能找到一个可微的代替函数,“对数几率函数(简称对率函数)”正是这样一个替代函数$$y=\frac{1}{1+e^{-z}}(3.17)$$ 上图可以看出对数几率函数是“Sigmoid函数”,将对数几率函数作为$g^{-}(\cdot )$可得到$$y=\frac{1}{1+e^{-(w^{T}x+b)}}(3.18)$$式(3.18)可变化为$$ln\frac{y}{1-y}=w^{T}x+b(3.19)$$将$y$视为样本$x$作为正例的可能性,$1-y$作为反例的可能性,两者的比值$$\frac{y}{1-y}(3.20)$$称为“几率”,反映了$x$作为正例的相对可能性。对几率取对数得到“对数几率”$$ln\frac{y}{1-y}(3.21)$$以上模型称为“对数几率回归”,虽说名称是回归,但其是分类任务。其直接对分类进行建模,无需假设数据分布;其不仅预测出类别,而且得到类别的近似概率;对数函数是任意阶可导函数,有很好的数学性质。
那么如何确定(3.18)中的$w$和$b$呢?将(3.18)中$y$视为类后验概率估计$p(y=1|x)$,(3.19)可写为$$ln\frac{p(y=1|x)}{p(y=0|x)}=w^{T}x+b(3.22)$$显然有$$p(y=1|x)=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}(3.23)$$$$p(y=0|x)=\frac{1}{1+e^{w^{T}x+b}}(3.24)$$于是,可通过“极大似然法”估计$w$和$b$。给定数据集$\left \{ (x_{i},y_{i}) \right \}_{i=1}^{m}$,对率回归模型最大化“对数似然”$$l(w,b)=\sum_{i=1}^{m}lnp(y_{i}|x_{i};w,b)(3.25)$$即令每个样本真实标记概率越大越好。令$\beta =(w;b)$,$\hat{x}=(x;1)$,则$w^{T}x+b$可简写为$\beta ^{T}\hat{x}$。再令$p_{1}(\hat{x};\beta )=p(y=1|\hat{x};\beta )$,$p_{0}(\hat{x};\beta )=p(y=0|\hat{x};\beta )=1-p_{1}(\hat{x};\beta )$,则(3.25)可重写为$p(y_{i}|x_{i};w,b)=y_{i}p_{1}(\hat{x_{i}};\beta )+(1-y_{i})p_{0}(\hat{x_{i}};\beta )(3.26)$将(3.26)带入(3.25),并根据(3.23)和(3.24)可知,最大化(3.25)等价于最小化$$l(\beta )=\sum_{i=1}^{m}(-y_{i}\beta_{T}\hat{x_{i}}+ln(1+e^{\beta^{T}\hat{x_{i}}}))(3.27)$$可根据梯度下降法、牛顿法求解得到$$\beta^{*}=\underset{\beta }{argmin}l(\beta )(3.28)$$以牛顿法为例,第$t+1$轮迭代解的更新公式为$$\beta^{t+1}=\beta^{t}-(\frac{\partial^{2}l(\beta )}{\partial \beta \partial \beta^{T}})^{-1}\frac{\partial l(\beta )}{\partial \beta }(3.29)$$关于$\beta $的一阶二阶导数为$$\frac{\partial l(\beta )}{\partial \beta }=\sum_{i=1}^{m}\hat{x_{i}}(y_{i}-p_{1}(\hat{x_{i}};\beta ))(3.30)$$$$\frac{\partial ^{2}l(\beta )}{\partial \beta \partial \beta ^{T}}=\sum_{i=1}^{m}\hat{x_{i}}\hat{x_{i}}^{T}p_{1}(\hat{x_{i}};\beta )(1-p_{1}(\hat{x_{i}};\beta ))(3.31)$$
线性判别分析(LDA)是一种经典的线性学习方法,在二分类最早由Fisher提出,因此也称为“Fisher线性判别”。LDA思想:给定训练数据集,将数据全部投影到一条直线上,要求使得同类样例投影点尽可能接近、异类样例投影点尽可能远离;对新样本进行分类时,将其投影到此直线上,根据投影点位置确定样本类别。下面是详细示意图
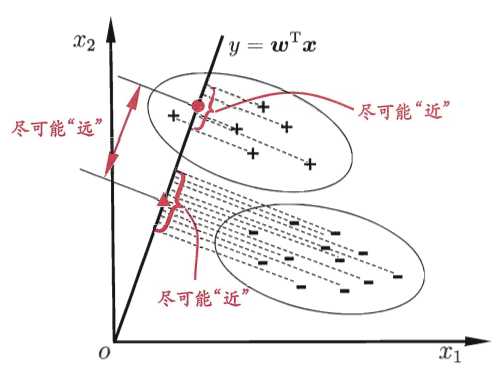
给定数据集$D=\left \{ (x_{i},y_{i}) \right \}_{i=1}^{m}$,$y_{i}\in \left \{ 0,1 \right \}$,令$X_{i}$、$\mu_{i}$、$\Sigma_{i}$分别为$i$类的集合、均值向量、协方差矩阵,其中$i\in \left \{ 0,1 \right \}$。将数据投影到直线$w$上,两类样本中心在直线上投影为$w^{T}\mu_{0}$和$w^{T}\mu_{1}$;将所有样本点都投影到直线上,两类样本协方差为$w^{T}\Sigma_{0}w$和$w^{T}\Sigma_{1}w$。由于直线为一维空间,因此上述四个值都是实数(可通过矩阵向量运算可知为实数)。
要使得同类样例投影点尽可能接近,可以让同类样例投影点协方差尽可能小(彼此之间更加紧密,太过于松散方法会变大),即$w^{T}\Sigma_{0}w+w^{T}\Sigma_{1}w$尽可能小;而要使异类样例投影点尽可能远,可以让两个类的中心距离尽量大,即$\left \| w^{T}\mu_{0}-w^{T}\mu_{1} \right \|_{2}^{2}$尽量大。此时同时考虑两者,一个要尽量小,一个要尽量大,即可得最大化目标$$J=\frac{\left \|w^{T}\mu _{0}-w^{T}\mu _{1} \right \|_{2}^{2}}{w^{T}\Sigma _{0}w+w^{T}\Sigma _{1}w}$$$$=\frac{w^{T}(\mu _{0}-\mu _{1})(\mu _{0}-\mu _{1})^{T}w}{w^{T}(\Sigma _{0}+\Sigma _{1})w}(3.32)$$定义“类内散度矩阵”$$S_{w}=\Sigma _{0}+\Sigma _{1}=\sum_{x\in X_{0}}(x-\mu_{0})(x-\mu _{0})^{T}+\sum_{x\in X_{1}}(x-\mu_{1})(x-\mu _{1})^{T}(3.33)$$以及“类间散度矩阵”$$S_{b}=(\mu _{0}-\mu _{1})(\mu _{0}-\mu _{1})^{T}(3.34)$$式(3.32)可写为$$J=\frac{w^{T}S_{b}w}{w^{T}S_{w}w}(3.35)$$这就是LDA欲最大化的目标,即$S_{b}$与$S_{w}$的“广义瑞利商”。
如何确定$w$呢?式(3.35)分子和分母都是$w$的二次项,因此(3.35)解与$w$长度无关(上下长度都一样,相除可以抵消)。因此可令$w^{T}S_{w}w=1$,式(3.35)等价于$$\underset{w}{min}-w^{T}S_{b}w(3.36)$$$$s.t. w^{T}S_{w}w=1$$由拉格朗日乘子法上式等价于$$S_{b}w=\lambda S_{w}w(3.37)$$注意到$S_{b}w$的方向恒为$\mu _{0}-\mu _{1}$,令$$S_{b}w=\lambda (\mu _{0}-\mu _{1})(3.38)$$带入(3.37)可得$$w=S_{w}^{-1}(\mu _{0}-\mu _{1})(3.39)$$由于求解$S_{w}^{-1}$可能不能求逆等问题,在实践中常对$S_{w}$进行奇异值分解,即$S_{w}=U\Sigma V^{T}$,这里$\Sigma$是实对角矩阵,对角线上元素是$S_{w}$的奇异值,然后由$S_{w}^{-1}=V\Sigma ^{-1}U^{T}$得到$S_{w}^{-1}$。
可以将LDA推广为多分类任务。假定存在$N$个类,且第$i$类示例数为$m_{i}$,定义“全局散度矩阵”$$S_{t}=S_{b}+S_{w}=\sum_{i=1}^{m}(x_{i}-\mu )(x_{i}-\mu )^{T}(3.40)$$其中$\mu$是所有示例的均值向量。将类内散度矩阵$S_{w}$重定义为每个类别的散度矩阵之和,即$$S_{w}=\sum_{i=1}^{N}S_{w_{i}}(3.41)$$其中$$S_{w_{i}}=\sum_{x\in X_{i}}(x-\mu _{i})(x-\mu _{i})^{T}(3.42)$$由(3.40)~(3.42)可得$$S_{b}=S_{t}-S_{w}=\sum_{i=1}^{N}m_{i}(\mu _{i}-\mu )(\mu _{i}-\mu )^{T}(3.43)$$显然,多分类LDA有多种方法实现:使用$S_{b},S_{w},S_{t}$三者中任何两种即可。常见的一种是采用优化目标$$\underset{W}{max}\frac{tr(W^{T}S_{b}W)}{tr(W^{T}S_{w}W)}(3.44)$$其中$W\in \mathbb{R}^{d\times (N-1)}$,$tr(\cdot )$表示矩阵的迹。(3.44)可通过广义特征值问题求解$$S_{b}W=\lambda S_{w}W(3.45)$$$W$的闭式解是$S_{w}^{-1}S_{b}$的$d‘$个最大非零广义特征值所对应的特征向量组成的矩阵,并且$d‘\leqslant N-1$。
若将$W$视为一个投影矩阵,多分类LDA将样本投影到$d‘$维空间,$d‘$常远小于$d$。于是可通过此投影减小样本点维数,因此LDA也被视为监督学习的降维技术。
一般情况下都是可以将二分类推广到多分类,利用二分类解决多分类问题。考虑$N$个类别$C_{1},C_{2},...,C_{N}$,多分类基本思路是“拆解”,即将多分类任务拆解为多个二分类任务。先进行拆解,然后每个小的二分类训练一个分类器;测试时,对这些分类器结果进行集成获得最终多分类结果。关键在于如何拆解,以及如何集成多个分类器。
经典拆分有三种:“一对一(OvO)”、“一对其余(OvR)”和多对多(MvM)。给定数据集$D=\left \{ (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m}) \right \}$,$y_{i}\in \left \{ C_{1},C_{2},...,C_{N} \right \}$。OvO将这$N$个类别两两配对,产生$N(N-1)/2$个二分类任务。测试阶段,新样本同时提交给所有$N(N-1)/2$个二分类器,最终通过投票产生结果:即把预测的最多的类别作为最终分类结果,如下图所示:总共4(4-1)/2=6个分类器,有三个分类器测试为$C_{3}$,所以最终结果为$C_{3}$。
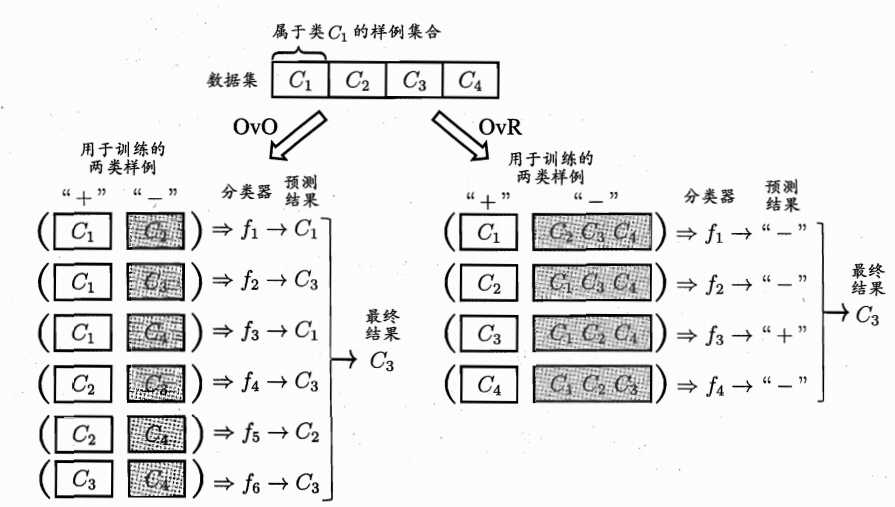
OvR每次将一个类作为正例、其余类作为反例训练出$N$个分类器。测试时若仅有一个分类器预测为正类,则对应的类别标记最为最终分类结果。如上图所示,只有分类器$f_{3}$将测试样例预测为“+”,此时类别为$C_{3}$。若有多个分类器预测为“+”,则考虑分类器置信度,置信度最大的类别标记作为分类结果。
MvM每次将若干个类作为正类,若干个其他类作为反类,显然OvO个OvR是其特例。MvM的正、反类构造必须有特殊的设计,不能随意选取。这里介绍一种常用MvM技术:“纠错输出码(ECOC)”。ECOC分为编码和解码两个过程,编码是对$N$个类别作$M$次划分,每次划分将一部分划分为正类、一部分划分为负类,形成一个二分类训练集;这样一共产生$M$个训练集,训练出$M$个分类器;解码是$M$个分类器分别对测试样本进行预测,这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果。
编码矩阵可以表示上面的情,分为二元码和三元码,前者将每个类别指定为正类(+1)或负类(-1),后者还可以指定停用类(0)。下图展示了相应的编码,在测试阶段,各分类器预测结果联合起来就形成了测试示例的编码,该编码与各类所对应的编码求距离,将距离最小编码所对应的类别作为预测结果。
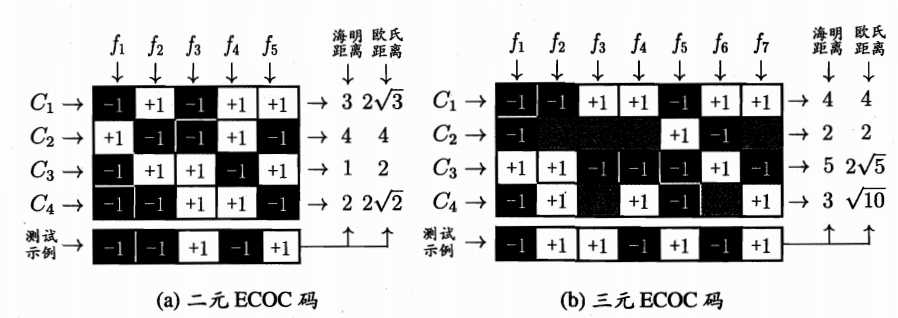
一般来说,对同一个学习任务,ECOC编码越长,纠错能力越强,因为中间如果有个别分类器预测错误,但是总体上不影响距离的计算,还是得到最小距离,那么ECOC就能很大程度上进行纠错。
前面介绍的分类方法都有一个共同假设,即不同类别的训练集数目差不多。如果不同类别的训练集数目相差很大,则会对学习过程造成困扰(毕竟1000个样本中只有1个正类,不用学习,随机猜测准确率都有99.9%)。类别不平衡是指分类任务中不同类训练样例数目差别很大的情况。
当我们使用线性方程$y=w^{T}x+b$对新样本$x$进行分类时,事实上使用预测出的$y$和一个阈值进行比较,例如$y>0.5$时判定为正类。$y$表达了正例的可能性,几率$\frac{y}{1-y}$反映了正例可能性与反例可能性之比,阈值设置为0.5恰表示为正反例可能相同,分类决策规则为$$\frac{y}{1-y}>1 则预测为正例(3.46)$$当训练集中正反例数目不同时,令$m^{+}$表示正例数目,$m^{-}$表示反例数目,则观测几率是$\frac{m^{+}}{m^{-}}$,观测几率就代表了真实几率。因此,只要分类器预测几率高于观测几率就应判定为正例,即$$若\frac{y}{1-y}>\frac{m^{+}}{m^{-}} 则预测为正例(3.47)$$但是,我们分类器是基于(3.46)进行决策,因此需对预测值进行调整,使其在基于式(3.46)决策时,实际是在执行(3.47)。只需令$$\frac{y‘}{1-y‘}=\frac{y}{1-y}\times \frac{m^{-}}{m^{+}}(3.48)$$这就是类别不平衡学习的一个基本策略——“再缩放”。
(以下均假设正类样例过少)再缩放难以实现,主要因为“训练集是真实样本总体的无偏采样”这个假设往往不成立。现有技术有三种做法:第一类是直接对训练集中反类样例进行“欠采样”,即去除一些反例使得正、反例数目相近;第二类是对训练集里正类样例进行过采样,即增加正例使得正、反例数目相近;第三类是直接基于原始训练集进行学习,但在用训练好的分类器进行预测时,将(3.48)嵌入到其决策过程中,称为“阈值移动”。
标签:导数 梯度下降 决策 最大的 正则 简单 上进 拆分 能力
原文地址:https://www.cnblogs.com/jiaojun520/p/10847835.html