标签:ann highlight python split none lda 显示图片 end lld
--判断一个患者的肿瘤是好是坏?
############################# 朴素贝叶斯实战--判断肿瘤是良性的还是恶性的 ####################################### #导入数据集拆分工具 from sklearn.model_selection import train_test_split #导入威斯康星乳腺肿瘤数据集 from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() print(‘\n\n\n‘) print(‘代码运行结果:‘) print(‘====================================\n‘) #打印数据集键值 print(cancer.keys()) print(‘\n====================================‘) print(‘\n\n\n‘)
代码运行结果: ==================================== dict_keys([‘data‘, ‘target‘, ‘target_names‘, ‘DESCR‘, ‘feature_names‘, ‘filename‘]) ====================================
#打印数据集中标注好的肿瘤分类 print(‘肿瘤的分类:‘,cancer[‘target_names‘]) #打印数据集中的肿瘤特征名称 print(‘\n肿瘤的特征:\n‘,cancer[‘feature_names‘])
肿瘤的分类: [‘malignant‘ ‘benign‘] 肿瘤的特征: [‘mean radius‘ ‘mean texture‘ ‘mean perimeter‘ ‘mean area‘ ‘mean smoothness‘ ‘mean compactness‘ ‘mean concavity‘ ‘mean concave points‘ ‘mean symmetry‘ ‘mean fractal dimension‘ ‘radius error‘ ‘texture error‘ ‘perimeter error‘ ‘area error‘ ‘smoothness error‘ ‘compactness error‘ ‘concavity error‘ ‘concave points error‘ ‘symmetry error‘ ‘fractal dimension error‘ ‘worst radius‘ ‘worst texture‘ ‘worst perimeter‘ ‘worst area‘ ‘worst smoothness‘ ‘worst compactness‘ ‘worst concavity‘ ‘worst concave points‘ ‘worst symmetry‘ ‘worst fractal dimension‘]
#将数据集的数值和分类目标赋值给X和y X,y = cancer.data,cancer.target #使用数据集拆分工具拆分为训练集和测试集 X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=38) print(‘\n\n\n‘) print(‘代码运行结果:‘) print(‘====================================\n‘) #打印训练集和测试集的数据形态 print(‘训练集数据形态:‘,X_train.shape) print(‘测试集数据形态:‘,X_test.shape) print(‘\n====================================‘) print(‘\n\n\n‘)
代码运行结果: ==================================== 训练集数据形态: (426, 30) 测试集数据形态: (143, 30) ====================================
#导入高斯朴素贝叶斯
from sklearn.naive_bayes import GaussianNB
#使用高斯朴素贝叶斯拟合数据
gnb = GaussianNB()
gnb.fit(X_train,y_train)
print(‘\n\n\n‘)
print(‘代码运行结果:‘)
print(‘====================================\n‘)
#打印模型评分
print(‘训练集得分:{:.3f}‘.format(gnb.score(X_train,y_train)))
print(‘测试集得分:{:.3f}‘.format(gnb.score(X_test,y_test)))
print(‘\n====================================‘)
print(‘\n\n\n‘)
代码运行结果: ==================================== 训练集得分:0.948 测试集得分:0.944 ====================================
print(‘\n\n\n‘)
print(‘代码运行结果:‘)
print(‘====================================\n‘)
#打印模型评分
print(‘模型预测的分类:{}‘.format(gnb.predict([X[312]])))
print(‘样本的正确分类是:‘,y[312])
print(‘\n====================================‘)
print(‘\n\n\n‘)
代码运行结果: ==================================== 模型预测的分类:[1] 样本的正确分类是: 1 ====================================
############################# 高斯朴素贝叶斯的学习曲线 #######################################
#导入学习曲线库
from sklearn.model_selection import learning_curve
#导入随机拆分工具
from sklearn.model_selection import ShuffleSplit
#导入numpy
import numpy as np
#导入高斯朴素贝叶斯
from sklearn.naive_bayes import GaussianNB
#导入画图工具
import matplotlib.pyplot as plt
#定义一个函数绘制学习曲线
def plot_learning_curve(estimator,title,X,y,ylim=None,cv=None,n_jobs=1,train_sizes=np.linspace(.1, 1.0, 5 )):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
#设定横轴标签
plt.xlabel("Training examples")
#设定纵轴标签
plt.ylabel("Score")
train_sizes,train_scores,test_scores = learning_curve(estimator,X,y,cv=cv,n_jobs=n_jobs,train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores,axis=1)
test_scores_mean = np.mean(test_scores,axis=1)
plt.grid()
plt.plot(train_sizes,train_scores_mean,‘o-‘,color="r",label="Training score")
plt.plot(train_sizes,test_scores_mean,‘o-‘,color="g",label="Cross-valldation score")
plt.legend(loc="lower right")
return plt
#设定图题
title = "Learning Curves (Naive Bayes)"
#设定拆分数量
cv = ShuffleSplit(n_splits=100,test_size=0.2,random_state=0)
#设定模型为高斯朴素贝叶斯
estimator = GaussianNB()
#调用我们定义好的函数
plot_learning_curve(estimator,title,X,y,ylim=(0.9,1.01),cv=cv,n_jobs=4)
#显示图片
plt.show()
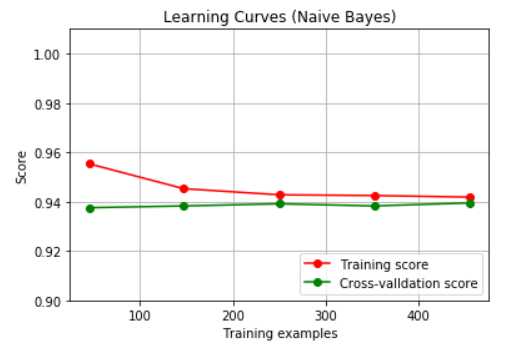
总结:
高斯朴素贝叶斯在预测方面,对于样本的要求并不是很苛刻,如果你的样本比较少的话,应该可以考虑使用朴素贝叶斯算法来建模.
相比起线性模型来说,朴素贝叶斯的算法的效率更高一点,这是因为朴素贝叶斯算法会把数据集中的各个特征看作完全独立的,而不考虑特征之间的关系关联关系.
在现在大数据时代,在超高维的数据集中,线性模型的训练时间可能会很长,所以朴素贝叶斯是一个很好的选择.
文章引自:《深入浅出python机器学习》
标签:ann highlight python split none lda 显示图片 end lld
原文地址:https://www.cnblogs.com/weijiazheng/p/10880557.html