标签:image code 行列式 mic 部分 ash 概念 出现 网上
在刚接触线性代数时,最先学到的是行列式,随之而来的就是矩阵。矩阵的出现过于突兀,当初学习时完全不清楚它的概念,更不要说还有矩阵乘法等各种奇怪的算术操作。于是从网上学习了各种矩阵概念,受益良多,在此总结一下学到的概念。
矩阵最早来自于方程组的系数及常数所构成的方阵。——百度百科
如此看来,矩阵和行列式还是有联系的,矩阵最初可能就是用来表示行列式用的
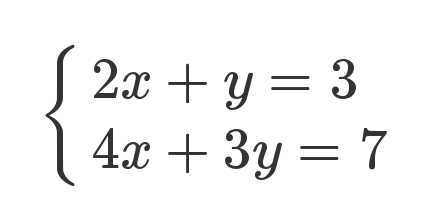
方程组
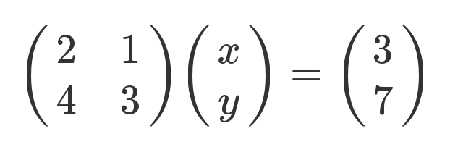
改写成矩阵的形式
然而矩阵的作用不仅限于此,它有着线性变换的作用,我们将通过分析矩阵乘法来详加解释
提起矩阵乘法,我们脑中浮现的可能是老师一遍遍强调的求法:一行乘一列。但这么算下来,根本没法理解这么做的意义,感觉就是将矩阵强行转换回行列式一样。但若将矩阵乘法转换为二维图像,就会发现矩阵实际上起到了线性变换的作用
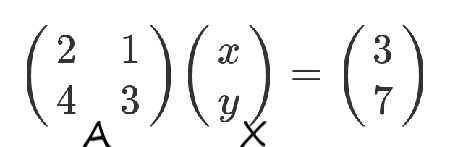
用A和x代替矩阵和未知量
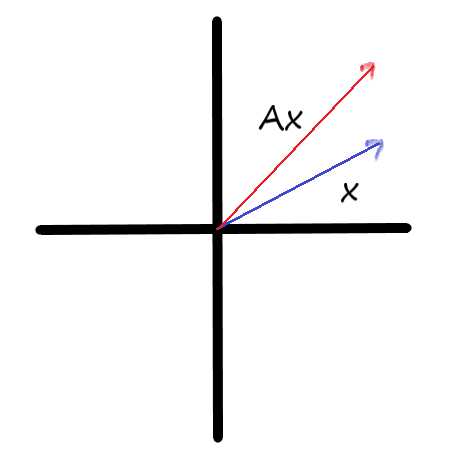
x在坐标轴中经矩阵变换后的图像
我们也可以将矩阵视为向量的基,这样看的话,向量的坐标值并没有改变,只是它所在的基改变了,所以这是一种线性的变化,所以矩阵也被称为线性映射。
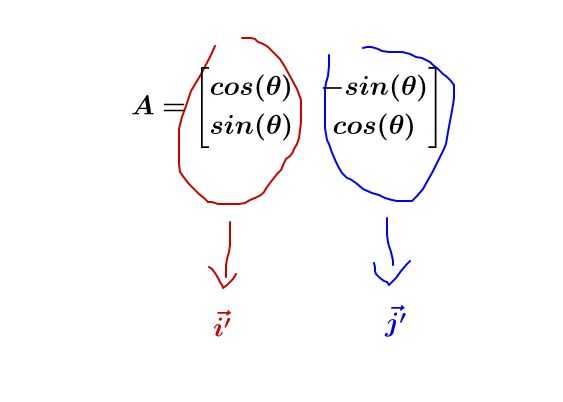
旋转矩阵没有改变原来的向量,只是改变了坐标系,我们可以用行列式推导这个过程
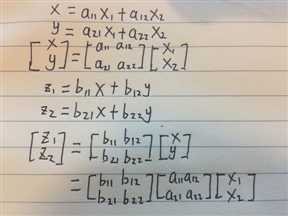
将x和y代入到z坐标系后发现其结果和矩阵乘法的结果一致
那么矩阵的变换作用是怎么样的,这个就留到矩阵特征值部分讲解
标签:image code 行列式 mic 部分 ash 概念 出现 网上
原文地址:https://www.cnblogs.com/matrixmlpforever/p/10886830.html