Kernels and image sets for an operator and its dual

标签：not   display   element   cal   space   from   play   sub   which   

Let $\mathcal{X}$ and $\mathcal{Y}$ be Hilbert spaces. Let $A: \mathcal{X} \rightarrow \mathcal{Y}$ be a bounded and linear operator. Then

$$
A(\mathcal{X})^{\perp} = \ker(A^*), \; \ker(A^*)^{\perp}=\overline{A(\mathcal{X})}.
$$

This relation can be illustrated in the following figure. Here we use blue color to represent the "effective mapping", i.e. from the orthogonal complement of the operator‘s  kernel to the operator‘s image set. And red color is used to represent the mapping from the operator‘s kernel to the zero element of the operator‘s range space. The orthogonal complement of a subset in a Hilbert space is a subspace, which is closed. Meanwhile, the image set of an operator is not necessarily closed. This is why there is a closure operation in $\ker(A^*)^{\perp}=\overline{A(\mathcal{X})}$.

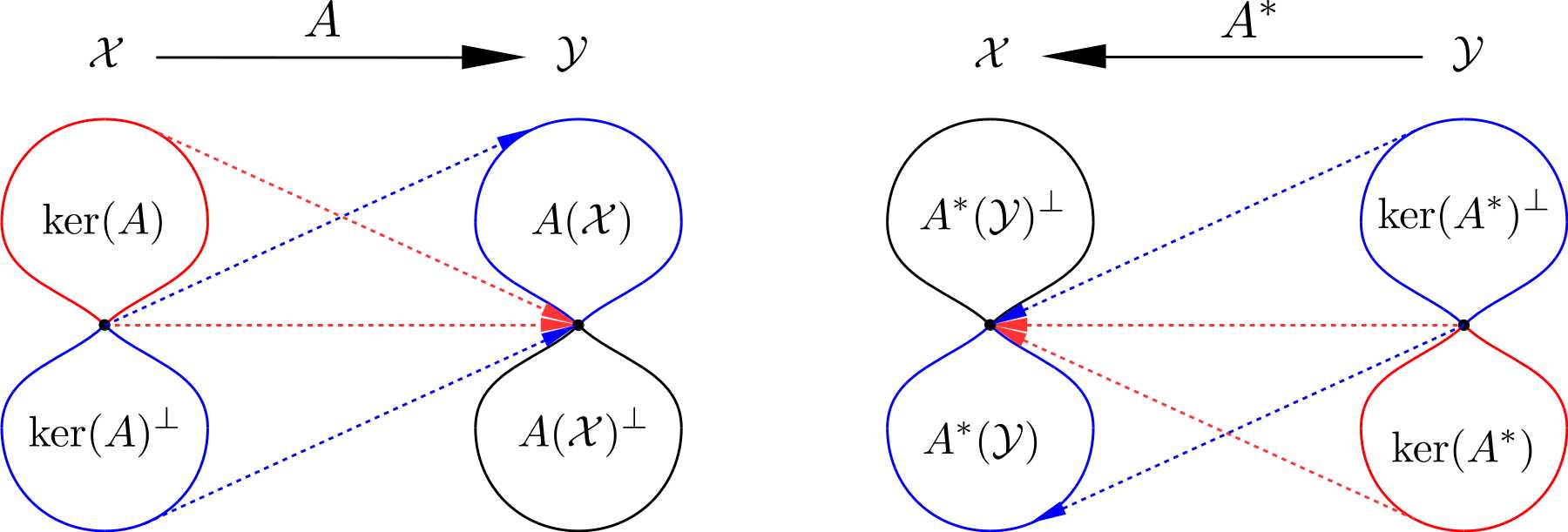
Kernels and image sets for an operator and its dual

标签：not   display   element   cal   space   from   play   sub   which   

原文地址：https://www.cnblogs.com/peabody/p/10887626.html