标签:cti 数据 val 需要 是什么 ought to lis 缺点 参考
弄清楚图 本章重点
1.邻接矩阵:表示顶点之间相邻关系的矩阵
邻接矩阵表示法的特点:
优点:容易实现图的操作,如:求某顶点的度、判断顶点之间是否有边、找顶点的邻接点等等。
缺点:n个顶点需要n*n个单元存储边; 空间效率为O(n2)。对稀疏图而言尤其浪费空间。
2.邻接表
(1)图的链式存储结构
(2)图的邻接表存储表示

1 #define MVNum 100//最大顶点数 2 3 typedef struct ArcNode//边结点 4 5 { 6 7 int adjvex;//该边所指向的顶点的位置 8 9 struct ArcNode *nextarc;//指向下一条边的指针 10 11 OtherInfo info;//和边相关的信息 12 13 }ArcNode; 14 15 typedef struct VNode//顶点信息 16 17 { 18 19 VerTexType data; 20 21 ArcNode *firstarc;//指向第一条依附于边的指针 22 23 }VNode,AdjList[MVNum];//AdjList表示邻接表类型 24 25 typedef struct 26 27 { 28 29 VerTexType vexs[MVNum]; //顶点表 30 31 ArcType arcs[MVNum][MVNum]; //邻接矩阵 32 33 int vexnum,arcnum; //图的当前点数和边数 34 35 }AMGraph;
3.图的遍历
图的遍历:从图中某个顶点出发游历图,访遍图中其余顶点,并且使图中的每个顶点仅被访问一次的过程。
!!!深搜和广搜
DFS:从图中某个顶点V0 出发,访问此顶点,然后依次从V0的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和V0有路径相通的顶点都被访问到
重点:(1)递归过程(2)为了区别顶点是否被访问,附设访问标志数组visited[n],其初值为“false”,一旦某个顶点被访问,则其相应的置被赋为“true”
BFS:在访问了起始点v之后,依次访问 v 的邻接点; 然后再依次访问这些顶点中未被访问过的邻接点; 直到所有顶点都被访问过为止。
重点:(1)分层搜索,不是递归(2)①从图中某个顶点v出发,访问v,并置visited[v]的值为true,然后将v 进队。② 只要队列不空,则重复下述处理: (1)队头顶点u出队。 (2)依次检查u的所有邻接点w,如果visited[w]的值为false,则访问w,并置visited[w]的值为true,然后将w 进队。
列出连通图

1 #include<iostream> 2 #include<queue> 3 4 using namespace std; 5 6 #define MAXNUM 15 7 bool check[MAXNUM] = {false}; 8 9 //建立邻接矩阵//Create Graph 10 int G[MAXNUM][MAXNUM] = {0}; 11 int N,E;//N为顶点数,E为边数 12 13 void DFS(int ); 14 int BFS(int ); 15 void ListComponentsDFS(); 16 void ListComponentsBFS(); 17 void isvisited(); 18 void BuildGraph(); 19 20 int main() 21 { 22 //建图 23 BuildGraph(); 24 //DFS遍历连通集 25 ListComponentsDFS(); 26 isvisited(); 27 //BFS遍历连通集 28 ListComponentsBFS(); 29 return 0; 30 } 31 32 33 void BuildGraph() 34 { 35 int i,j; 36 int v1,v2;//每一行的顶点名称 37 38 cin >> N >> E;//N是顶点数,E是边数 39 40 for(i = 0;i< E;i++)//每行输出一个连通集 41 { 42 cin >> v1 >> v2;//InsertEdge 43 G[v1][v2] = 1;//联通 置为1 44 G[v2][v1] = 1; 45 46 } 47 } 48 49 //DFS 50 void DFS(int v) 51 { 52 check[v] = true;//已被访问置为true 53 cout << v <<" "; 54 for(int i=0;i<N;i++) 55 { 56 if(G[v][i] && !check[i])//如果联通且该点没有被访问过 57 { 58 DFS(i); 59 } 60 } 61 62 } 63 64 void ListComponentsDFS() 65 { 66 int i; 67 for(i=0;i<N;i++) 68 { 69 if(!check[i]) 70 { 71 cout <<"{ "; 72 DFS(i); 73 cout << "}" << endl; 74 } 75 } 76 } 77 78 //初始化visited 79 void isvisited() 80 { 81 for(int i=0;i<N;i++) 82 { 83 check[i] = false; 84 } 85 } 86 87 //BFS 88 int BFS(int v) 89 {//队列 90 queue <int> q; 91 q.push(v); 92 int x; 93 check[v] = true; 94 while(!q.empty()) 95 { 96 x = q.front();//x本身被访问过 97 q.pop(); 98 cout << x << " "; 99 for(int i=0;i<N;i++) 100 { 101 if(!check[i]&&G[x][i]){ 102 check[i] = true; 103 q.push(i); 104 } 105 } 106 } 107 } 108 109 110 void ListComponentsBFS() 111 { 112 int i; 113 for(i = 0;i<N;i++) 114 { 115 if(!check[i]) 116 { 117 cout <<"{ "; 118 BFS(i); 119 cout << "}" <<endl; 120 } 121 } 122 }
1.列出连通图的思路:
①先将连通图的构造出来

1 void BuildGraph() 2 { 3 int i,j; 4 int v1,v2;//每一行的顶点名称 5 6 cin >> N >> E; 7 8 for(i = 0;i< E;i++) 9 { 10 cin >> v1 >> v2;//InsertEdge 11 G[v1][v2] = 1;//联通 置为1 12 G[v2][v1] = 1; 13 14 } 15 }

②先是DFS

1 void DFS(int v) 2 { 3 check[v] = true;//已被访问置为true 4 cout << v <<" "; 5 for(int i=0;i<N;i++) 6 { 7 if(G[v][i] && !check[i])//如果联通且该点没有被访问过 8 { 9 DFS(i); 10 } 11 } 12 13 } 14 15 void ListComponentsDFS() 16 { 17 int i; 18 for(i=0;i<N;i++) 19 { 20 if(!check[i]) 21 { 22 cout <<"{ "; 23 DFS(i); 24 cout << "}" << endl; 25 } 26 } 27 } 28
ListComponentsDFS() :用for循环判断结点是否被访问过,若被访问了
DFS:则是用for循环判断结点之间是否连通,并且输出连通的结点

③isvisited

1 void isvisited() 2 { 3 for(int i=0;i<N;i++) 4 { 5 check[i] = false; 6 } 7 } 8
因为之后要用BFS再进行一次遍历,所以要将之前置为访问过的全部置为未被访问的,这一步还挺关键的
④最后BFS
其实这个地方跟上一章的树有点相似,是用了队列的方法,将头元素入队又出队

1 int BFS(int v) 2 {//队列 3 queue <int> q; 4 q.push(v); 5 int x; 6 check[v] = true; 7 while(!q.empty()) 8 { 9 x = q.front();//x本身被访问过 10 q.pop(); 11 cout << x << " "; 12 for(int i=0;i<N;i++) 13 { 14 if(!check[i]&&G[x][i]){ 15 check[i] = true; 16 q.push(i); 17 } 18 } 19 } 20 } 21 22 23 void ListComponentsBFS() 24 { 25 int i; 26 for(i = 0;i<N;i++) 27 { 28 if(!check[i]) 29 { 30 cout <<"{ "; 31 BFS(i); 32 cout << "}" <<endl; 33 } 34 } 35 }

遇到的困难:
在这次的列出连通图中遇到困难有的①“void value not ignored as it ought to be”刚开始我不知道这句话是什么意思我就上网百度了一下,后面发现是因为在BFS函数中本来我是定义为void的,但是后来我又在后面对它了值,最后需要输出队头元素,所以我就将其改成了int类型就搞定了
②“a function-definition is not allowed here before ‘{‘ token”这个问题就是括号没有匹配对的问题 只要细心一点就可以检查出来了,但是刚开始看到function-definition is not allowed 我以为是我没有申明函数,就将main函数和其他函数的位置调换了一下,又在前面申明了函数,但是后来发现还是不行,就开始从{这个问题下手,终于找到了问题所在
③遇到最最最大的困难就是BFS和DFS的区别
刚开始我没有弄清楚BFS和DFS的概念,在画BFS的输出表示时,我觉得很奇怪因为按我的想法是输出{0 1 7 4 2}因为我认为7在4之前入队,是遍历完0的所有连接点再遍历1的连接点,所以7比4先入队
我甚至画了一张图 但是是错误的,
但是是错误的,
后来我明白了,遍历了0的一个连接点后,再接着遍历1 的连接点,所以7在4 之后入队,正确的应该是这样的
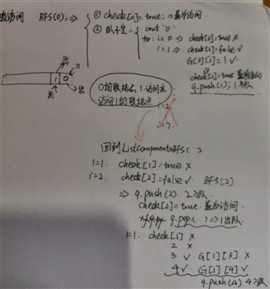
所以我们一定要弄清楚概念:深搜:一个节点的所有邻接点都访问完了之后,再访问下一个邻接点
广搜:一个节点的一个邻接点访问完后,就可访问下一个邻接点
目标完成情况:
1.上次是希望pta上的题能够在ddl前比较久的时间完成,这次是做到了,但是我觉得不是很好,因为其实这一章图我觉得很难,我有些懵讲真的,所以这章的两道编程题我都是在网上搜到答案后,搞懂,然后改了一些方法写的,特别是列出连通图的BFS那个地方,网上大部分方法是构造了一个叫quene的数组,来进行队列的功能,但是我觉得上章老师教的方法queue<int>q很好,所以我就改了这部分,用了这个方法来写。
2.下次的目标:我觉得老是从网上参考现有程序这样对自己的能力可能提升不够,希望下次的编程题能够先有自己的思路,而不是急着在网上在答案,来看别人的思路,而是真的能够将自己的思路写成代码实现
PS:这次我改了一下图片的格式,不知道会不会清楚一点,希望能够比上次有进步啦~
标签:cti 数据 val 需要 是什么 ought to lis 缺点 参考
原文地址:https://www.cnblogs.com/snowlxy/p/10886829.html