标签:成语 部分 color 单词 循环 cout cst length 递归
▍题目分析
单词接龙是一个与我们经常玩的成语接龙相类似的游戏,现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”(每个单词都最多在“龙”中出现两次),在两个单词相连时,其重合部分合为一部分,例如beast和astonish,如果接成一条龙则变为beastonish,另外相邻的两部分不能存在包含关系,例如at和atide间不能相连。
输入的第一行为一个单独的整数n(n≤20)表示单词数,以下n行每行有一个单词(只含有大写或小写字母,长度不超过20),输入的最后一行为一个单个字符,表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在。
只需输出以此字母开头的最长的“龙”的长度。
5 at touch cheat choose tact a
23
确定算法:乍一看这道题,至少想不到有什么较优的方法,那么怎么办呢?最简单的方法:打暴力!!!可是,又该怎么打暴力呢?一看题目就头疼,如何确定接龙的方法?这是最麻烦的事。那么此时就要用到搜索,因为搜索的本质正是将繁琐的过程简化。这里我们将会使用深度优先搜索求解。
▎题解方法
这道题就先想想大概接龙的方法吧:输入→从开始的字符判断有没有能接到的龙→如果有字符串能接到,则接上去→再算出接龙后的长度→找到所有接龙情况中的最大值。
1 cin>>n; 2 for(int i=1;i<=n;i++) 3 cin>>str[i]; 4 cin>>str[n+1];//这里把开始的字符存在了所有字符串的后面一个,也可以换成一个变量
1 void dfs(string s,int length_now)//s是之前接好的龙,length_now是当前接龙的总长度 2 { 3 //do something 4 for(int i=1;i<=n;i++) 5 { 6 if(vis[i]>1) continue; 7 else 8 { 9 int add=check(s,str[i]);//当前字符串与原来字符串的重叠部分的大小 10 if(add!=0)//即两个字符串有重叠部分 11 { 12 //do something 13 } 14 } 15 } 16 17 }
但是怎么知道重合长度呢?这是一个麻烦事。当然我们是不知道重合长度的,所以呢?就先假设一个长度,再看看原先龙的尾巴能不能和这个字符串的头对上,如果能就返回。再考虑以下几个问题:
A:从1到两个字符串中长度最小的一个,否则容易发生数组越界。
A:从1开始不断增大,因为重合长度越小,接出的龙就越长。
A:我们需要依靠一一对应关系。从0开始(因为字符串默认下标是从0开始的)到假设重合长度-1(同理)依次来判断一个字符串的首元素和另一个字符串的尾元素是否相等。那么如果判断首元素的字符串的每一位为b[ j ],那么判断尾元素的字符串的每一位为a[ a.length( ) - i + j ],这可能有点难理解,但是只要多画图就明白了。
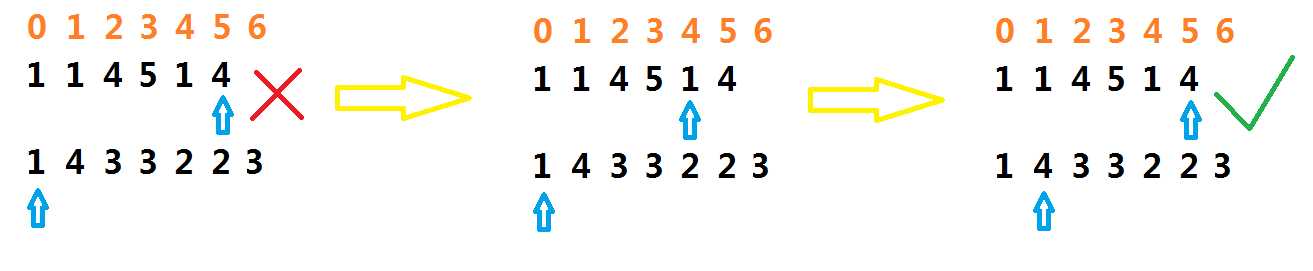
A:需要。分两种情况:一种是没有重合长度,要返回0;另一种是两个字符串中长度最小的长度为1,那样因为循环的问题会直接返回0 。
1 inline int check(string a,string b) 2 { 3 int p=min(a.length(),b.length()); 4 for(int i=1;a.length()==1? i<=p:i<p;i++) 5 { 6 bool flag=true; 7 for(int j=0;j<i;j++) 8 { 9 if(a[a.length()-i+j]!=b[j]) 10 { 11 flag=false; 12 break; 13 } 14 } 15 if(flag==true) return i; 16 } 17 return 0; 18 }
5.算出所有接龙情况中的最长长度:只要每次递归时不断比较就行了……
1 length=max(length,length_now);
▎Code speaks louder than words!
1 #include<iostream> 2 #include<cstring> 3 #include<cmath> 4 using namespace std; 5 int n,length=0,vis[1000]={0};string str[1000]; 6 inline int check(string a,string b) 7 { 8 int p=min(a.length(),b.length()); 9 for(int i=1;a.length()==1? i<=p:i<p;i++) 10 { 11 bool flag=true; 12 for(int j=0;j<i;j++) 13 { 14 if(a[a.length()-i+j]!=b[j]) 15 { 16 flag=false; 17 break; 18 } 19 } 20 if(flag==true) return i; 21 } 22 return 0; 23 } 24 void dfs(string s,int length_now) 25 { 26 length=max(length,length_now); 27 for(int i=1;i<=n;i++) 28 { 29 if(vis[i]>1) continue; 30 else 31 { 32 int add=check(s,str[i]); 33 if(add!=0) 34 { 35 vis[i]++; 36 dfs(str[i],length_now+str[i].length()-add); 37 vis[i]--; 38 } 39 } 40 } 41 42 } 43 int main() 44 { 45 cin>>n; 46 for(int i=1;i<=n;i++) 47 cin>>str[i]; 48 cin>>str[n+1]; 49 dfs(str[n+1],1); 50 cout<<length<<endl; 51 return 0; 52 }
标签:成语 部分 color 单词 循环 cout cst length 递归
原文地址:https://www.cnblogs.com/TFLS-gzr/p/10884932.html