标签:def 访问 src empty 就是 lis 深度优先搜索 onclick list
本周我们学习了图这一结构,图是一种比线性表和树更为复杂的数据结构,因此我也花费了更多的时间在书本上。
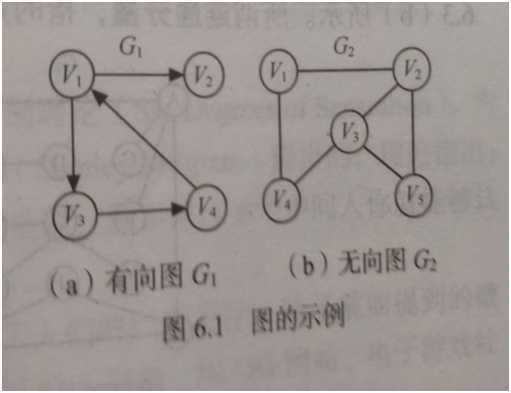
图可由两个集合V和E组成,其中V是顶点的集合,E是边的集合。对于图而言,可根据边集E是否为有向或无向,将图分为有向图和无向图,如下
 除此之外,图的基本术语也需要我们熟记并且掌握,见下图
除此之外,图的基本术语也需要我们熟记并且掌握,见下图


了解了图的基本定义以及基本术语,接下来就要开始学习图的存储结构。不同于之前的数据结构,图没有顺序存储结构,但可以借助二维数组来表示元素,即邻接矩阵表示法,而由于图任意两个顶点间都存在关系这一特点,图的链式存储有多种,有邻接表、十字链表和邻接多重表。
1、邻接矩阵

#define MaxInt 10000 //表示极大值,即∞ #define MVNum 100 //最大顶点数 typedef char VerTexType;//假设顶点的数据类型为字符型 typedef int ArcType; //假设边的权值类型为整型 typedef struct { VerTexType Vexs[MVNum]; //顶点表 ArcType arcs[MVNum] [MVNum]; //邻接矩阵 int vexnum,arcnum; //图的当前点数和边数 }AMGraph;
2、邻接表

#define MvNum 100 //最大顶点数 typedef struct ArcNode //边结点 { int adjvex; //该边所指向的顶点的位置 struct ArcNode *nextarc;//指向下一条边的指针 }ArcNode; typedef struct VNode //顶点信息 { VertexType data; ArcNode *firstarc; //指向第一条依附该顶点的边的指针 }VNode,AdjList[MvNum]; //AdjList表示邻接表类型 typedef struct { AdjList Vertices; //一维数组 int vexnum,arcnum; //图的当前顶点数和边数 }Graph;
接下来我们学习了图的遍历,根据搜索路径的方向,可分为两种遍历图的路径:深度优先搜索和广度优先搜索。DFS类似树的先序遍历,是树的先序遍历的推广

void DFS(Graph a,int b) //深度优先搜索 { visited[b]=true; //令顶点对应的visited数组为true,表示该顶点已被访问过 cout<<b<<" "; //输出顶点编号及空格 for(int i=0;i<a.vexnum;i++) { if(a.arcs[b][i]==1 && visited[i]==false)DFS(a,i); //若顶点对应的邻接点未被访问,则递归调用DFS函数 } }
BFS则类似树的层次遍历

void BFS(Graph a,int b) //广度优先搜索 { int temp; //定义参数 while(!q.empty()) //若队列不为空 { temp=q.front(); //取队头元素值为temp q.pop(); //队头元素出队 cout<<temp<<" "; //输出temp值及空格 for(int i=0;i<a.vexnum;i++) { if(a.arcs[temp][i]==1 && visited[i]==false) //若顶点对应的邻接点未被访问,则邻接点入队 { q.push(i); //邻接点入队 visited[i]=true; //邻接点对应的visited数组取true,表示已被访问 } } visited[b]=true; //第一次入队的顶点对应的visited数组值取true,表示已被访问 } }
在对图的应用里,我们学习了最小生成树,其中普利姆算法和克鲁斯卡尔算法是用来构造最小生成树的算法。
1. Prim算法 普里姆算法 ——加点法
时间复杂度 O(n²) 适用于稠密图
主要步骤:在所有 u∈ U, v∈V-U 的边(u,v)属于E中找一条权值最少的边(u0,v0),并入集合TE(N上最小生成树中边的集合),同时v0并入U
2. Kruskal算法 克鲁斯卡尔算法 ——加边法
时间复杂度 O(e log e) 适用于稀疏图
初始状态为只有n个顶点而无边的非连通图 T = { V , { } } 每个顶点自成一个连通分量
主要步骤:在E中选择权值最小的边,若该边依附的顶点落在不同连通分量上(即不形成回路),则将此边并入T,否舍去此边而选择下一条权值最小的边
在这章的学习当中,我参考了书籍《数据结构·c语言版》,其中我了解了很多需要记住的定义,会对写代码时的注释提供许多的帮助。下面几周的目标,还是以加强写代码的能力为主,其次就是要能够清楚地知道某种结构的具体定义,最好能够用自己的话来叙述出来。
标签:def 访问 src empty 就是 lis 深度优先搜索 onclick list
原文地址:https://www.cnblogs.com/lsg666/p/10888812.html