第6章小结

标签：mgr   图的遍历   ++   依次   www   get   div   void   基础   

本章知识要点：

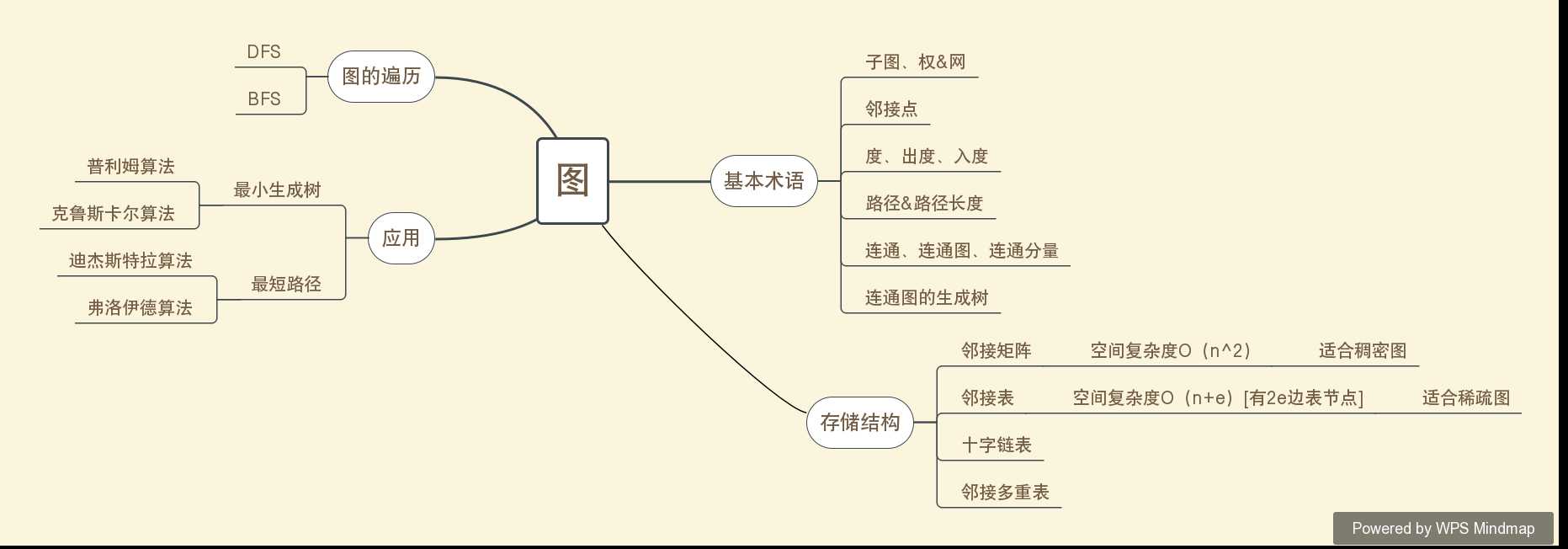
图的遍历重点：DFS：（和树的先序遍历类似）（1）递归过程（2）为了区别顶点是否被访问，附设访问标志数组visited[n],其初值为0，一旦某个顶点被访问，则其相应的置被赋为1；

BFS：（和树的层次遍历类似）（1）分层搜索（2）①从图中某个顶点v出发，访问v，并置visited[v]的值为1，然后将v 进队。② 只要队列不空，则重复下述处理： （1）队头顶点u出队（2）依次检查u的所有邻接点w，如果visited[w]的值为0，则访问w，并置visited[w]的值为1，然后w 进队

邻接表表示法的优缺点：

 （1）便于增加和删除结点；便于统计边的数目；空间效率高。

 （2）不便于判断顶点之间是否有边；不便于计算有向图各个顶点的度。

邻接矩阵表示方法的优缺点：

（1）便于判断两个顶点之间是否有边；便于计算各个顶点的度，对于有向图，第i行元素之和就是顶点i的出度，第i列元素之和就是顶点i的入度。

（2）不便于删除和增加顶点；空间复杂度高。

列出连通图：

在做这道题的时候一开始觉得应该会很简单，但实际上做的时候还是遇到了一点困难滴。一开始是DFS的因为顶点的visited数组没有置1标记为已经访问过，所以DFS一直输出不了。还有因为定义visited数组为全局变量，所以一开始没有在两种遍历前重置visited数组，所以最后就输出错误。这里我get到了新知识memset函数，这里我参考了https://www.cnblogs.com/heyonggang/p/3419574.html了解了memset函数的使用方法，重置了visited数组后就解决了输出错误的情况。

其中在如何表达for（i=x的第一个邻接点；i存在；i=x的相对于i的下一个邻接点）时不知道怎么表达。因为题目没有边的权值，所以我一开始也没有给边的权赋值，在这个表达就出现了困难。后来参考了网上的代码，知道了可以将边的权值赋为1，表示两个顶点存在，所以最后将代码改成了这样：

DFS中：

 1 void DFS(AMGraph G, int v)
 2 {//从顶点v出发，深度优先搜索遍历连通图G
 3     visited[v]=1;//标记v已被访问 
 4     cout<<v<<" "; 
 5     for(int i=0;i<G.vexnum;++i)
 6     {
 7         if(G.arcs[i][v]==1 && (visited[i]==0))//邻接点i存在且没有被访问过 
 8         DFS(G,i);//对v的尚未访问的邻接顶点i进行递归调用DFS
 9     }        
10 }

BFS中：

1 for(int i=0;i<G.vexnum;++i)
2             if(G.arcs[i][u]==1 && visited[i]==0) 
3             {//如果顶点i存在且没有被访问过 
4                 visited[i]=1;
5                 q.push(i);//i入队 
6             }//if

下面是完整代码：

列出连通集

上次定的要熟练树的遍历、多看看哈夫曼树的目标也有好好落实了，感觉上一章掌握的还是不错滴，在多画图分析后哈夫曼树也可以好好消化掉了，这次的目标：希望自己能够完成拯救007这道题，巩固好图的基础，这一章比树要难了，所以要多花时间好好消化一下课上的内容:D  !!

第6章小结

标签：mgr   图的遍历   ++   依次   www   get   div   void   基础   

原文地址：https://www.cnblogs.com/liulijun1551/p/10891401.html