Blog 5.第六章 图的认识

标签：调用   alt   表头   出栈   art   因此   sharp   ted   不同   

一、图的存储结构

图的数组(邻接矩阵)存储表示：

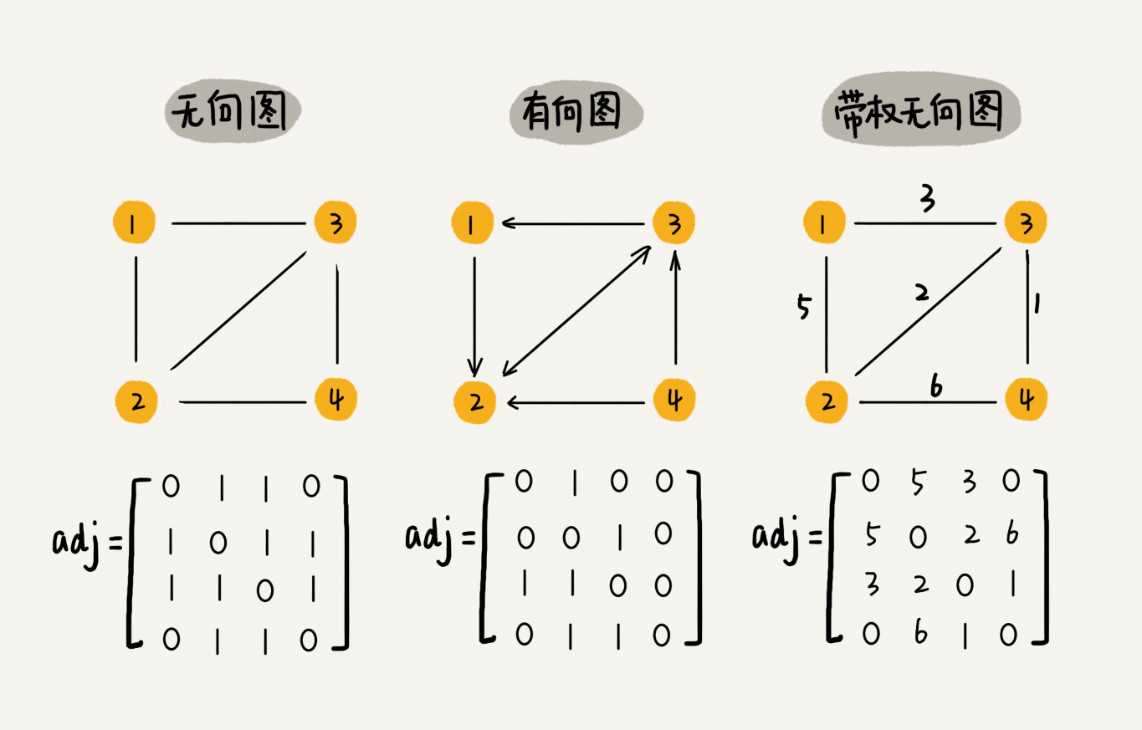
优点：1/0表示方便

缺点：不利于增加删除顶点

特殊：时间复杂度较高，不稀疏图；不过在无向图，可利用下三角形来压缩处理空间。

例子1：

（需要辅助数组）

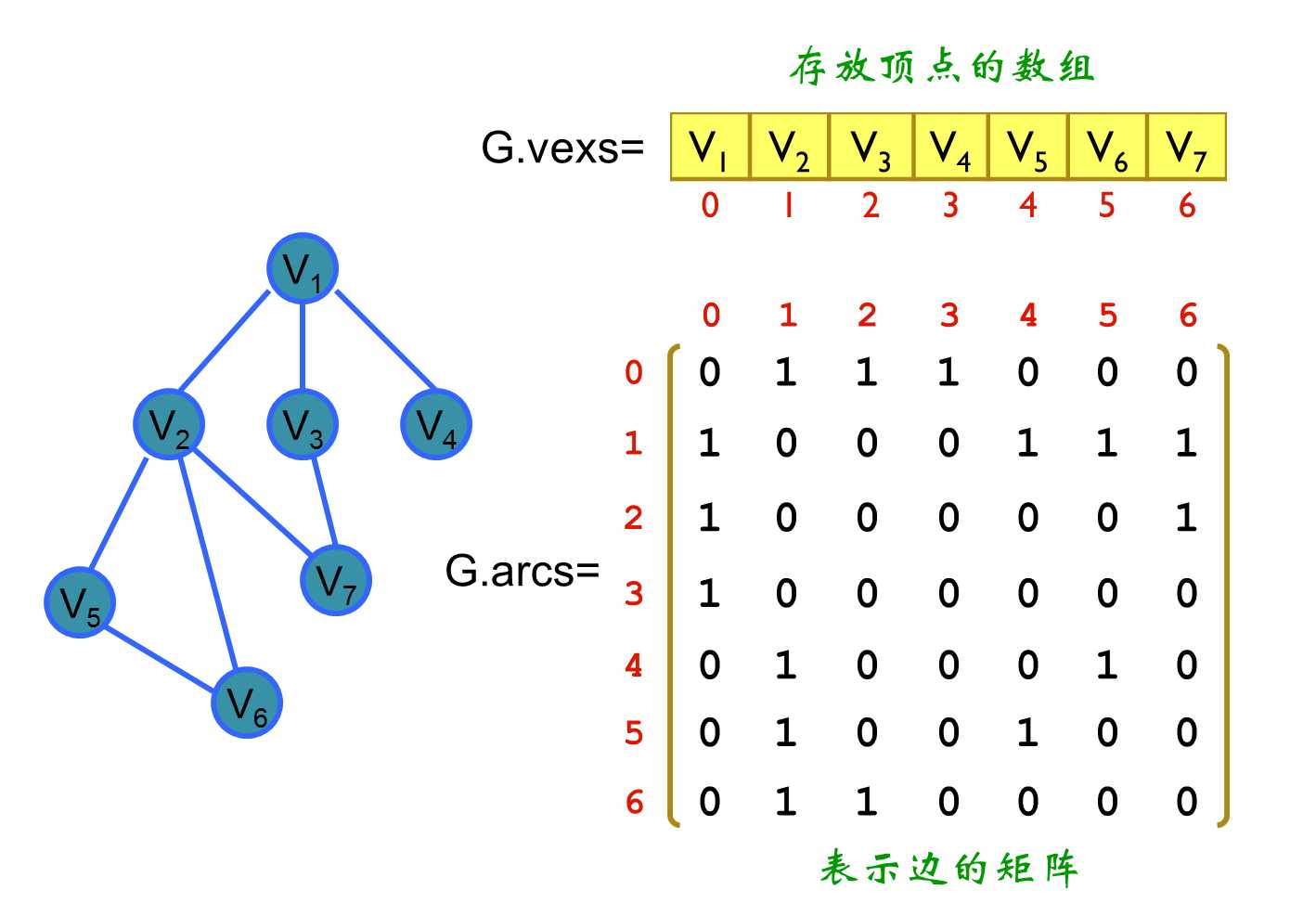
来源：https://www.cnblogs.com/XMU-hcq/p/6065057.html

例子2：

（1/0替换成当下边的权值）

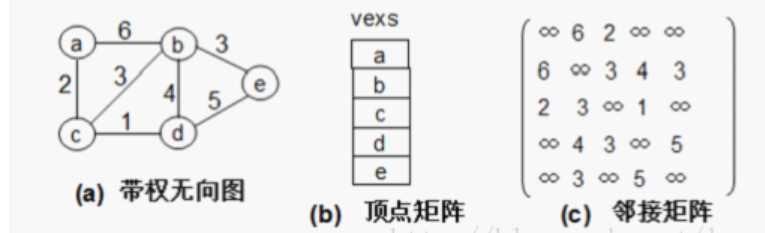
来源：https://blog.csdn.net/luoweifu/article/details/9270693

图的邻接表存储表示：

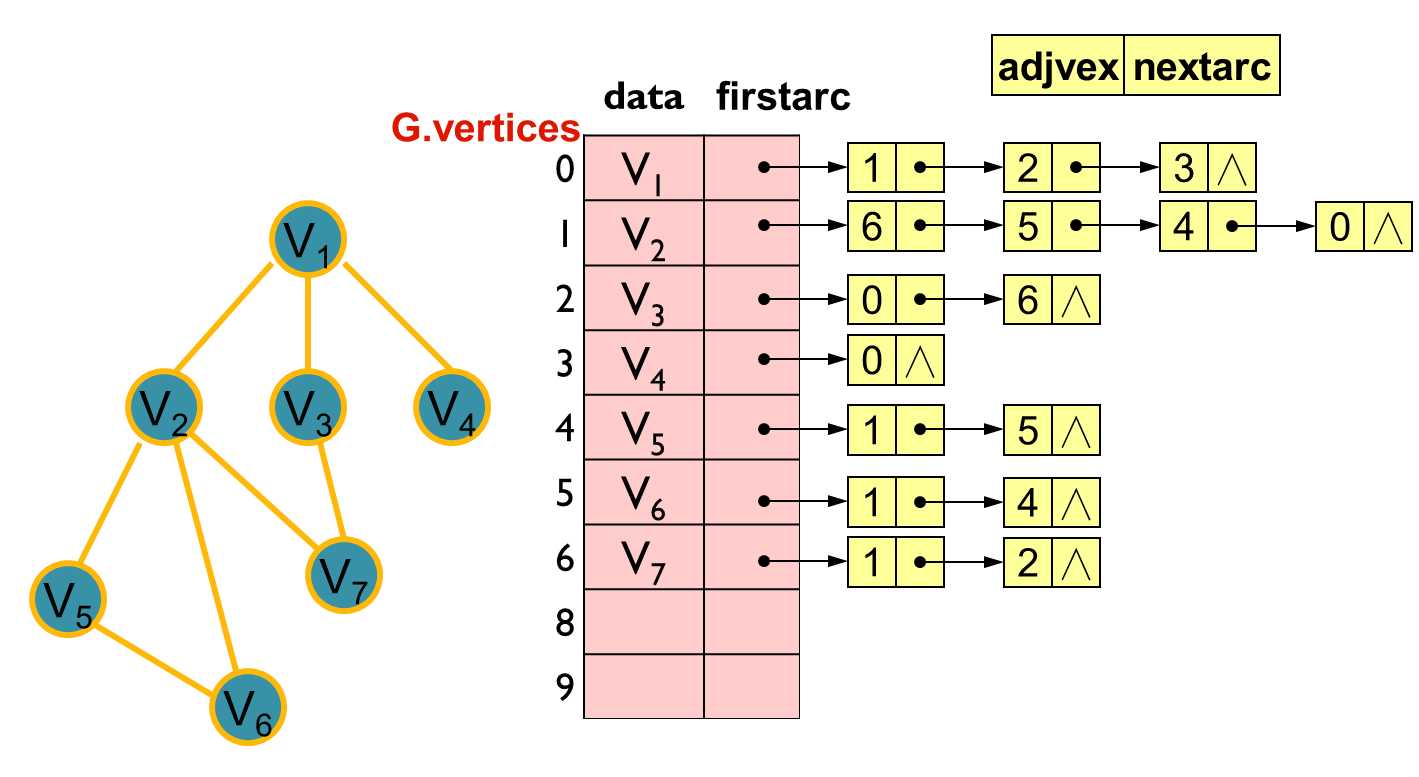
来源：https://www.cnblogs.com/XMU-hcq/p/6065057.html

包括：表头结点表(按顺序存放)，边表（链表）

优点：增删方便

缺点：不利于判断顶点之间是否有边（需要一一遍历），且不便于计算度。

备注：在对图的增加删除操作时，便可链接到前面所学的链表增加删除操作。

并且增加顶点用头插法，增加删除操作时注意while循环条件有所不同：

前者是（p!=NULL）插入有n+1种情况

后者是（p->next=NULL）删除有n种情况

二、图的两种遍历深度搜索、广度搜索

深度搜索个人认为和树的先序搜索逻辑相似，广度搜索与层次遍历相似。

而搜索有分基于哪种存储结构以及是否采用递归来体现，并且遍历连通图还是非连通图。

备注：由于顶点只能被访问一次，因此可借助辅助数组、队列等来判断。

void DFS(Graph G, int v) {
   // 从顶点v出发，深度优先搜索遍历连通图 G
    visited[v] = True;   
    for(w=FirstAdjVex(G, v);
             w>=0; w=NextAdjVex(G,v,w))
        if (!visited[w]) DFS(G, w);     
              // 对v的尚未访问的邻接顶点w
              // 递归调用DFS
} // DFS

 非递归实现：
visited[i]=false;//栈S初始化
访问顶点v；visited[v]=true;//顶点v入栈S
while(S!=NULL)
 {
 x=栈S的顶元素//不出栈；
if(visited[w])
cout<<w；
visited[w]=1；
 w进栈;
  else
 x出栈;
}

广度搜索：

类比层次以及上述栈的实现：

1.从图中某个顶点v出发，访问v，并置visited[v]的值为true，然后将v 进队。
2.只要队列不空，则重复下述处理：
   （1）队头顶点u出队。
   （2）依次检查u的所有邻接点w，如果visited[w]的值为false，则访问w，并置visited[w]的值为true，然后将w进队。

三、图的应用

最小生成树：普里姆算法、克鲁斯卡尔算法。

区别：

普里姆算法
 归并顶点，与边数无关，适于稠密网。
克鲁斯卡尔算法
 归并边，适于稀疏网。

普里姆算法操作:

设有连通网络 N = { V, E }：
1. 构造一个只有 n 个顶点，没有边的非连通图 T = { V, 空集 }, 每个顶点自成一个连通分量。
2.  在 E 中选最小权值的边,若该边的两个顶点落在不同的连通分量上，则加入 T 中；否则舍去，重新选择。
3.重复下去，直到所有顶点在同一连通分量上为止。

克鲁斯卡尔算法操作：

选择与刷新的过程：

1.初始化：计算从源点v0到T中各顶点vk的当前长度。
2.选择：在集合T中选取当前长度最短的一条最短路径（v0......vk），将vk加入到顶点集合S中。
3.更新：对T中其余各条路径进行调整：
若在图中存在弧（u,vk），且（v0,...,u）+（u,vk）<（v0,...,vk）,则以路径（v0,...u,vk）代替（v0,...,vk）。
   反复进行第2第3步，直至求出源点到其余各顶点的最短路径长度。

四、近期回顾及接下来目标

1、选了图以后，很多知识可以迁移到之前所学内容，接下来需要在实操中不断回顾复习。

2、递归算法使用的不够灵活，需要再加强本层思考的能力。

3、老话题，保持手感，每日代码计划！

4、快步走多回头。

Blog 5.第六章 图的认识

标签：调用   alt   表头   出栈   art   因此   sharp   ted   不同   

原文地址：https://www.cnblogs.com/gzq18/p/10891310.html