测试用例（正交排列法）

标签：混合   说明   das   使用   png   rowspan   情况   平原   案例   

一、应用场合

　　有很多的控件，而且每个控件有多个取值的情况下，要考虑不同控件不同取值的组合

　　——如何使用最少、最优化的数据组合达到最大的测试覆盖。

二、和因果图法的区别：

　　因果图：适用于控件组合较少的（20种以下），要比较全面的考虑所有情况（或主要情况）。

　　正交排列法：适用于控件组合数量庞大，而从代码角度讲有没必要全部测试。

正交表

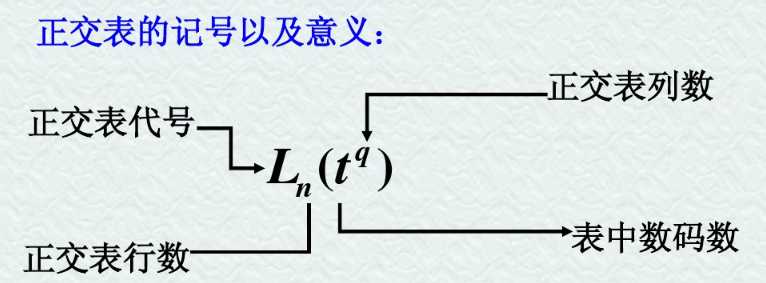
一种特制表，一般正交表记为：

• n：表示的是行数，也就是测试组合的次数
• t： 表示要测控件内包含的取值个数（各因素的水平数，即各因素的状态数）
• q：表示列数，即控件的个数（因素的个数，或因子的个数）

三、如何使用

　　1、分析需求——列出所有的控件和取值。——列出表格

　　2、根据控件的个数和控件的取值，选择一个合适的正交表：

　　　　（1）根据控件的个数，决定正交表的“次幂”（正交表的列数）例：4个控件——4次幂（4列）

　　　　（2）根据每个控件的取值个数，决定正交表的“底”（正交表中允许出现的最大值）例：每个控件有 3 个取值——底为3

　　3、把正交表中的列名和取值（1、2、3…）用控件名称和控件的真正取值替代

　　　　（1）把列名用控件名称替代

　　　　（2）把每列中的取值（1、2…）使用对应的控件真正的取值替代

　　4、根据正交表编写用例

　　　　把正交表的每一行转换成一条用例

 说明：

　　这些组合是经过数学推理出来的最少、最优化的用例

　　如果时间允许，最好再补充一些用例

正交表的局限性：（不一样的取值叫做混合正交表）

　　正交表个数有限，并基本要求控件取值个数相等

1、公平原则：使每个控件的每个取值参与组合的次数尽量相同

2、均匀原则：在所有的组合中挑选数据时，应该均匀零星的选取，而不要只从某个局部选

五、案例

每个控件的取值不相同

1、控件的个数决定次幂，如果没有，找一个最接近的（一般选大一点的） 4个控件——4次幂

2、如何选“底”

　　方案1：少数服从多数原则——有更多的控件取值相同的有 2 个控件取值为 3 ——选底为“3”

　　方案2：取值个数最多原则——看哪个控件取值最多，最多有 4 个 值——底为“4”

测试用例（正交排列法）

标签：混合   说明   das   使用   png   rowspan   情况   平原   案例   

原文地址：https://www.cnblogs.com/eric88/p/10848163.html