标签:纠错 divide 检验 校验码 time width 除法 传输 nbsp
1.奇偶校验法:
奇校验,数值部分各个位上数的和与校验位的和应是一个奇数,即,1的个数为奇数个,包括校验位。常用于同步传输。
偶校验,包括校验位有偶数个1,常用于异步传输或低速传输。
通常是在每个字节后增加一个附加位(奇偶校验位),即每个字节发送九位数据。
缺点,数位的错误以及偶数个位的错误检测不出来,无法定位错误。
例:
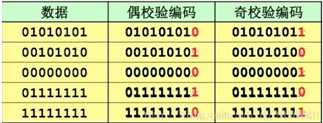
2.循环冗余校验法:
循环冗余(CRC)检验:数据M后面添加供差错检验用的n位冗余码,然后构成一个帧发送出去,一共发送(k+n)位。【模2运算求n:M÷P=Q…R,n即R】,校验时除以P(模2运算),余数R为0,则接受,不为0,则判定这个帧有差错。
具体:
在发送端,先把数据划分为组,假定每个组k个比特。现假定待传送的数据M=101001(k=6)。CRC运算就是在数据M后面添加供差错检验用的n位冗余码,然后构成一个帧发送出去,一共发送(k+n)位。在要发送的数据后面加n位的冗余码,虽然增加了数据传送的开销,但却可以进行差错检测。
这n位冗余码可以通过下面的方法得出。用二进制的模2运算进行2^n乘M的运算,即在M后面添加n个0。得到k+n位的数除以收发双方事先商定的长度为(n+1)位的除数p(p也可叫做生成多项式G,没固定),得出商是Q,余数是R(n位,比p少一位)。
例:

M=101001(k=6),假定除数p=1101(n=3,n比除数p少一位,即n为3位).经模2除法运算(实际上是除数和被除数做异或运算)后的结果是:商Q=110101(这个商并没有什么用),而余数R=001,这个余数R就作为冗余码拼接在M之后发送出去,这种为了进行检错而添加的冗余码常称为帧检验序列FCS,因此加上FCS后发送的帧是101001001(一共K+n位)。
在接收端把接收到的数据以帧为单位进行CRC检验:把收到的每一帧都除以同样的除数P(模2除法),然后检查得到的余数R。
如果在传输过程中无差错,那么经过CRC检验后得出的余数R肯定是0。
但如果出现误码,那么余数R仍等于0的概率是非常小的。
总结:
(1)若得出的余数R=0,则判定这个帧没错,就接受。
(2)若余数R!=0;则判定这个帧有差错(但无法确定是哪一位或者或者哪几位出现了差错),就丢弃。
再例如:

备注:
模2运算:一种二进制算法,CRC校验技术中的核心部分。与四则运算相同,模2运算也包括模2加、模2减、模2乘、模2除四种二进制运算。
与四则运算不同的是模2运算不考虑进位和借位(等同于“异或”运算),即模2加法是不带进位的二进制加法运算,模2减法是不带借位的二进制减法运算。
例:

3.海明码:
设数据有n位,校验码有x位。则校验码一共有2x种取值方式。其中需要一种取值方式表示数据正确,剩下2x-1种取值方式表示有一位数据出错。因为编码后的二进制串有n+x位,因此x应该满足 2x-1 ≥ n+x (备注:http://www.cnblogs.com/lesroad/p/8688634.html)
标签:纠错 divide 检验 校验码 time width 除法 传输 nbsp
原文地址:https://www.cnblogs.com/GodSince/p/10891903.html