朴素贝叶斯

标签：原理   ima   概率   idt   不清晰   nbsp   概率分布   函数   arg max   

　　为什么朴素贝叶斯如此朴素？主要由于它假定所有的特征在所有的数据集上是同等重要和独立的。这个假设在现实世界中是不真实的，所以说朴素。朴素贝叶斯（naive bayes），简单的假设特征条件独立，现实中独立的东西是不存在的，但是相关性较小的事物比较多的，于是贝叶斯往往能取得很好的效果。下面看下朴素贝叶斯的内容。

一、朴素贝叶斯的基本原理

　　朴素贝叶斯通过对训练集数据集学习联合概率分布P(x,Y)。

　　先验概率分布：P（Y=c_k）,k=1,2... 先验概率可以通过训练实例进行计算

　　条件概率分布：P(X=x|Y=c_k )=P(x₁,x₂, ...x_n|Y=c_k) 这概率公式比较难计算，参数指数级。

　　由于朴素贝叶斯假设条件，X互相独立同分布故：

　　　　P(X=x|Y=c_k) = P(X₍₁₎=x₁|Y=c_k)..P(X(n)=x_n|Y=c_k) = ∏ P(X_(i)|Y=ck)              （1）

　　所以我们需要求解的目标：

                          （2）

     把（1）式代入（2）中可得朴素贝叶斯的基本公式：

      朴素贝叶斯的分类器也可以表示为：

           y=f(x) = arg max(P(Y=c_k|X=x)

二、贝叶斯分类器的推导

  看到贝叶斯分类器的写法，感觉道理很简单，但具体怎么得来的还是有点不清晰,下面看下具体由来。

朴素贝叶斯后验概率最大化，这等价于期望风险最小化。选择合页损失函数：

式中的分f(x)是分类函数，。期望风险可以表示为：

朴素贝叶斯

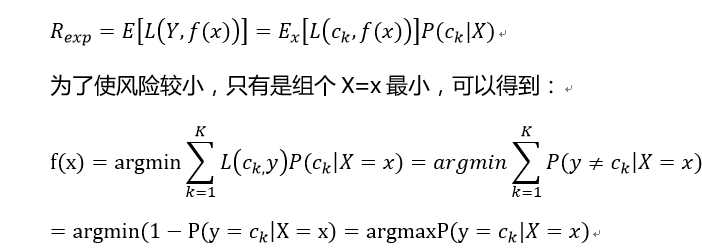
标签：原理   ima   概率   idt   不清晰   nbsp   概率分布   函数   arg max   

原文地址：https://www.cnblogs.com/haosu/p/10903363.html