标签:connect 实现 邻接 邻接表 res count 分析 符号 png
第一部分:JML小结
一、入门关键字小结
1.引导词:
requires :接下来部分的入口要求
assignable :在该程序中可修改的变量
ensures :后面是对该函数运行结束后的要求
also exception_behavior :接下来是出现异常的处理部分
signals : 对应抛出的异常
2.转义词:
\nothing :(一般用在assignable中,表示都不可修改)
\everything :(一般用在assignable中,表示都可修改)
\old :该函数修改前某变量的值
\result : 该函数的返回值
3.符号:
== :相等
==> : 前为真,则后为真;前为假,后的正确性无所谓
二、JML工具链
应用开源的JML工具链对代码进行编译,若程序没能实现JML规范中的提出的要求,则会抛出异常,从而可用于检验是否实现规格的要求。
第二部分:程序分析
概述:
这三次作业是通过给定的规格来完成程序, 相当于已经清晰给定了实现要求和结果来完成程序。
第一次:Path和PathContainer
一、分析自己程序结构
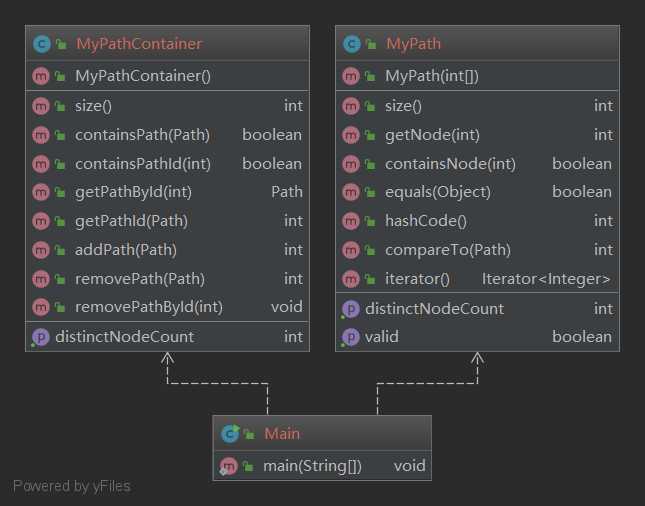
如图所示是我构建的类与之间的结构:
Path类中基本和规格要求的一致,只是为了方便起见,将存储节点的结构由规格中的静态数组改成了ArrayList。
PathContainer类中为了将getDistinctNodeCount()计算时的复杂度从O(n^2)降低,在该类中分别设置了三个HashMap用于存储,分别代表:path到pathId的映射,pathId到path的映射,以及每个节点到其出现次数的映射。从而通过虽然add和remove类指令复杂度变为了O(n),但getDistinctNodeCount()的复杂度降低到了O(1)。
二、自己的bug
由于这次基本规格内的表达方式写,也不涉及时间限制,故我没被发现bug
三、发现别人的bug
这次也没发现别人的bug
第二次作业、增加Graph
一、 分析自己的程序
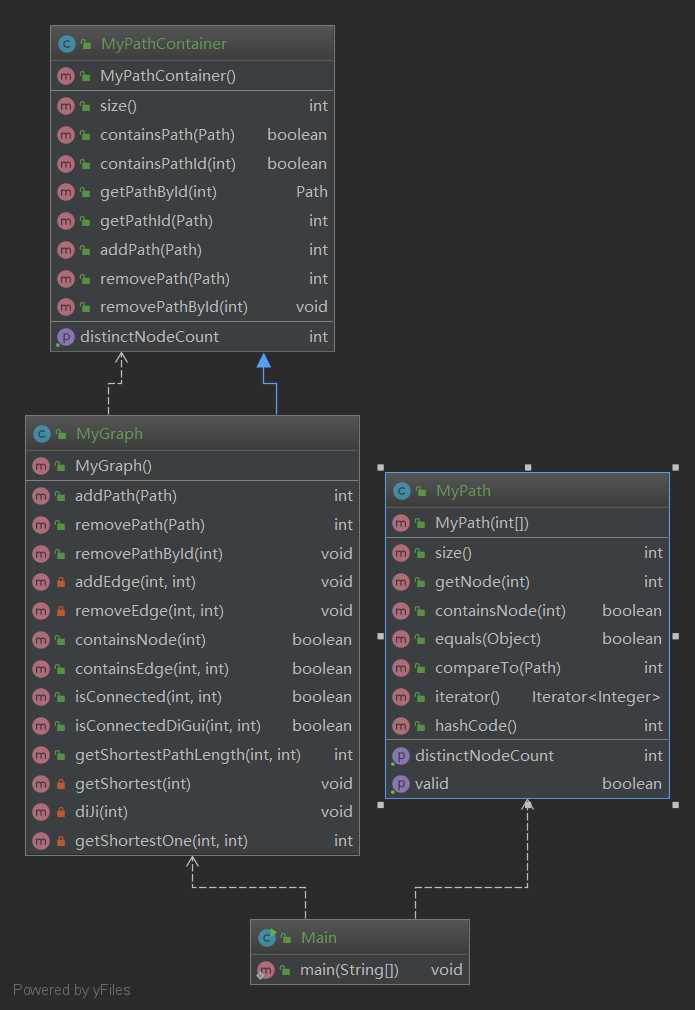
这次增加了Graph类,需要在原来的基础上“判断边存在”“判断连通”“求最短路径”等操作。
我的Main、MyPath、MyPathContainer三个类都没有进行变动,在MyGraph中继承了MyPathContainer。
具体实现中最大的难点在于“求最短路径”,在这里我采用了迪杰斯特拉算法:在add、remove时根据path生成图的邻接表graph,进而再使用迪杰斯特拉算法即可实现
具体流程是:
二、自己的bug
根据我本次的算法,在重复利用之前算过的最短路径时,需要先判断是否存在,但在判断时我出现了bug:只判断了起始点存在就断定存在,未判断终止点,从而出现了bug
三、 发现别人的bug
这次我们组内同学出现的bug包括:在remove时报了空指针错误,以及与我类似的判断两点是否邻接时出现的bug
第三次作业、多部电梯的调度
一、 分析自己结构
1.需求分析
这次作业需要新增MyRailwaySystem类,相应增加实现的功能包括:计算最少换乘、最少不满意度、最少票价、连通块个数。
这基本可以分成两个部分:最少…问题都可以视作最短路径问题的变式类似处理。
另一部分是计算连通块个数,这可以根据上次作业完成的“判断两点是否连通”来完成:取每条路径的第一个点,若和已经遍历过的路径都不连通,则可判断该点属于一个新连通块。
2.算法分析
主要需要重点考虑算法的是最短路径变式问题的算法,我采用了完全图算法:
先对每个Path进行Floyd算法,求出一个以最短路径为边的完全图,将每个边加上换乘所需权值;
再将其加入大图(包含已有所有顶点的),对大图中两点采用相应的最短路径算法,对得到的结果再减一次权值即可得到最终结果
解释:
每个Path生成完全图后已经完成了内部乘坐,除第一次外,之后每走一条边都需要换乘,所以可以直接采用迪杰斯特拉或弗洛伊德进行求最小值
3.具体实现
如下图是我的结构
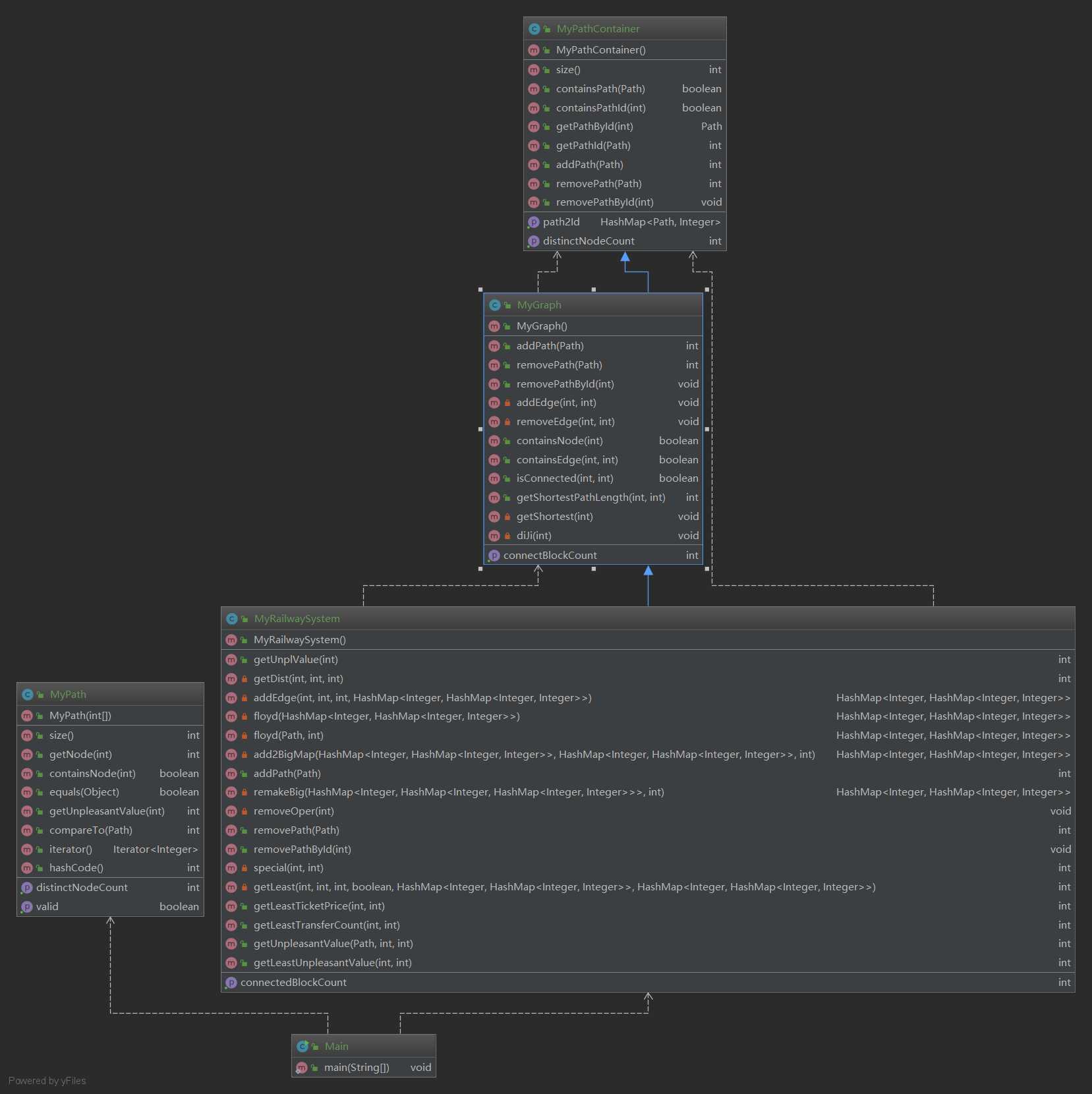
实现流程:
add:
1、 对新加入的path三种情况分别跑Floyd,得到三个最短路径集合,存入对应路径集
2、 分别该每条边加上对应的换乘权值,加入大图中
3、 修改三种对应的change
remove:
1、 从存储的路径集中删去该path
2、 重新生成大图
3、 修改对应change
getLeast:
1、 判断存储最小值的HashMap(finalDist)是否存在指定路径:(借助该finalDist和change)
2、 若存在、返回结果
3、 若不存在、对大图跑Floyd,将结果存入finalDist,修改change为false
二、 自己的bug
这次暴露出来的bug是上次遗留的祖传的bug:对重复add时,会两次将路径加入图中,导致我强测被hack到了好多点
三、 别人的bug
很可惜,这次没有找到别人的bug
第三部分 可进一步优化部分
第三次作业我这次类内部的结构写的不是很好,完全变成了面向过程的思路,对于处理最小值问题可以再新建一个类进行处理。
标签:connect 实现 邻接 邻接表 res count 分析 符号 png
原文地址:https://www.cnblogs.com/vegetables99/p/10905933.html