OO第三单元总结

标签：十分   无向图   索引下标   做了   接口   ros   boolean   映射   边界条件   

OO第三单元——JML与规格化设计

2019-05-22

JML语言及应用工具链

JML理论基础

　　JML（Java Modeling Language）是一种行为接口规格语言，用于对Java程序进行规格化设计。通过JML及其支持工具，不仅可以基于规格自动构造测试用例，并整合了SMT Solver等工具以静态方式来检查代码实现对规格的满足情况。

　　一般而言，JML有两种主要用法：

• 开展规格化设计。这样交给代码实现人员的将不是带有二义性的自然语言描述，而是逻辑严密的规格，从而实现设计与实现的分离。

• 针对已有的代码实现，书写其对应的规格，从而提高代码的可维护性。

JML应用工具链

 　　与 JML 相配套的很多应用工具能够支持JML的编译和检查，还有一些单元测试生成工具，例如OpenJML，JMLUnit，JMLUnitNG等等。

• OpenJML：一款提供JML语言检查的开源编译器，可以检查JML语法、根据JML对代码实现进行静态检查。
• JMLUnitNG：一款根据JML自动构造样例的测试生成工具，用于进行单元化测试。由实践知生成的样例偏向于边界条件的测试。

JMLUnitNG测试类与测试

• JMLUnitNG测试类

　　暂时没研究出来怎么用本次作业的Graph类生成测试样例，于是先试了试最简单的方法。

public class Main {
    //@ requires true;
    //@ ensures \result == a * b;
    public static int mult(int a,int b) {
        return a * b;
    }

    public static void main(String[] args) {
        mult(3,6);
    }
}

　　利用JMLUnitNG生成的测试样例如下：

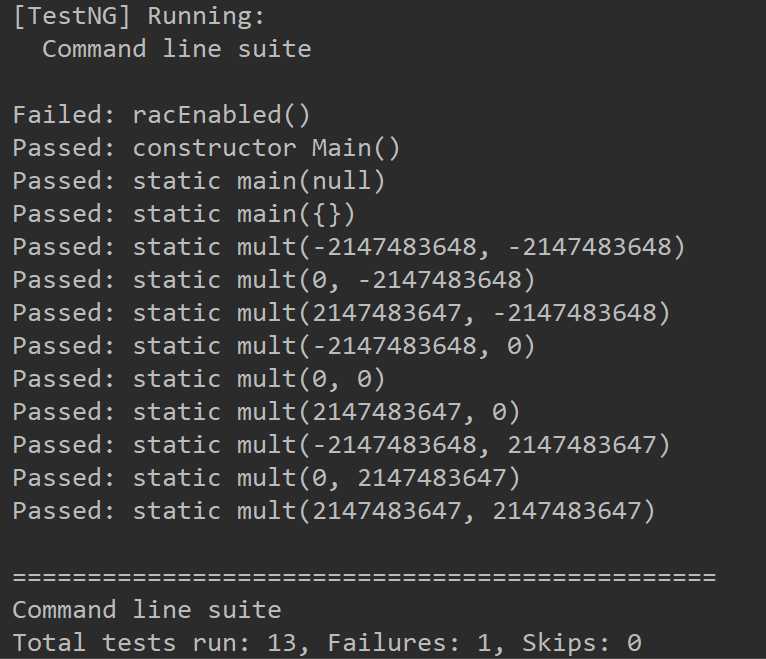
　　可见生成的样例更偏向于边界条件的测试。

• 测试：JUnit与对拍

 　　简单谈谈这一单元的测试。在这一单元中我尝试了用JUnit构造单元测试，并对RailwaySystem的几个计算换乘、票价、不满意度的方法进行了测试。通过自己构造测试样例可以排除一些特定条件下的bug，比如环路等一些特殊情况；但缺点是必须人为给出expected的值与actual值进行对比，因此只能做到小规模的单元测试。然而涉及到强测这样大批量上千条的指令，跟同学进行对拍显然是更好的选择。

架构设计梳理与BUG分析

第九次作业：路径管理系统（PathContainer）

• 类图

• 架构设计

　　本次作业需要实现两个容器类Path和PathContainer，也是后两次作业的基础。

　　整体较为简单，唯一需要注意的是时间复杂度的控制，由于查询类指令占据了3000条指令中的绝大部分，需尽可能降低查询方法的复杂度。为此，对关于路径及id的查询构建了分别以Path和id为key的HashMap（注意自定义对象需重写hashcode）。关于不同节点的查询，在Path中应用了HashSet元素不重复的特性；在PathContainer中存储了<节点，出现次数>的HashMap（nodeCount），并把节点的增删分散在addPath、removePath、removePathById修改类方法中。这样查询方法的复杂度就基本为O（1）。


• BUG分析

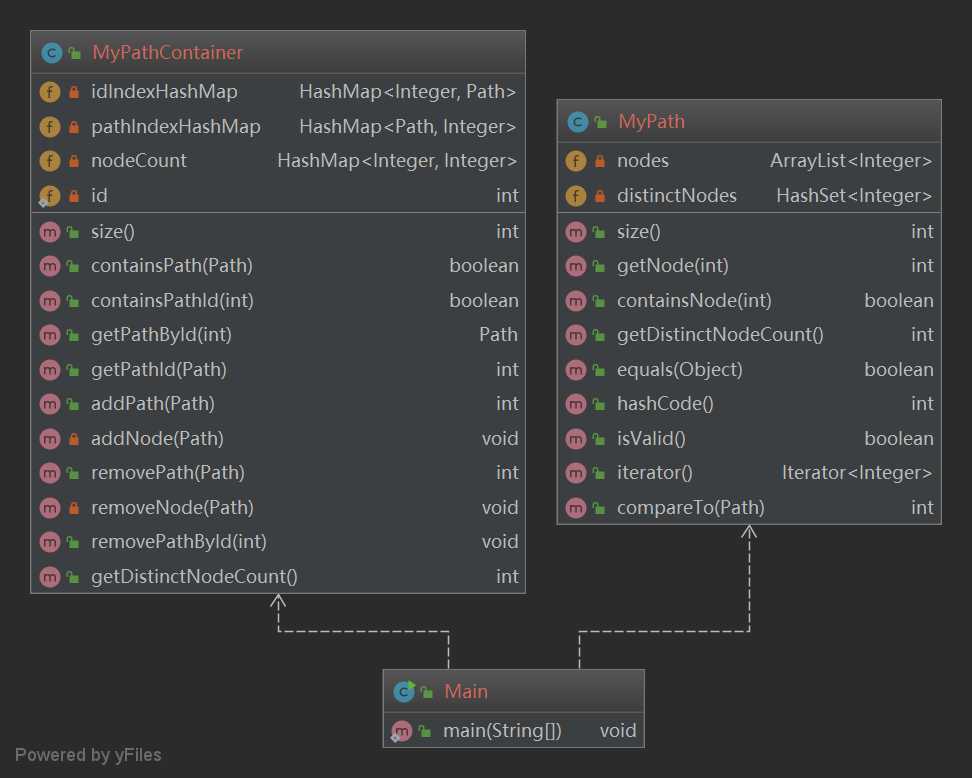
　　由于本次作业较为简单，强测和互测中均没有出现bug，而且一个互测屋的设计几乎一样，嗯……

第十次作业：无向图系统（Graph）

• 类图

• 架构设计

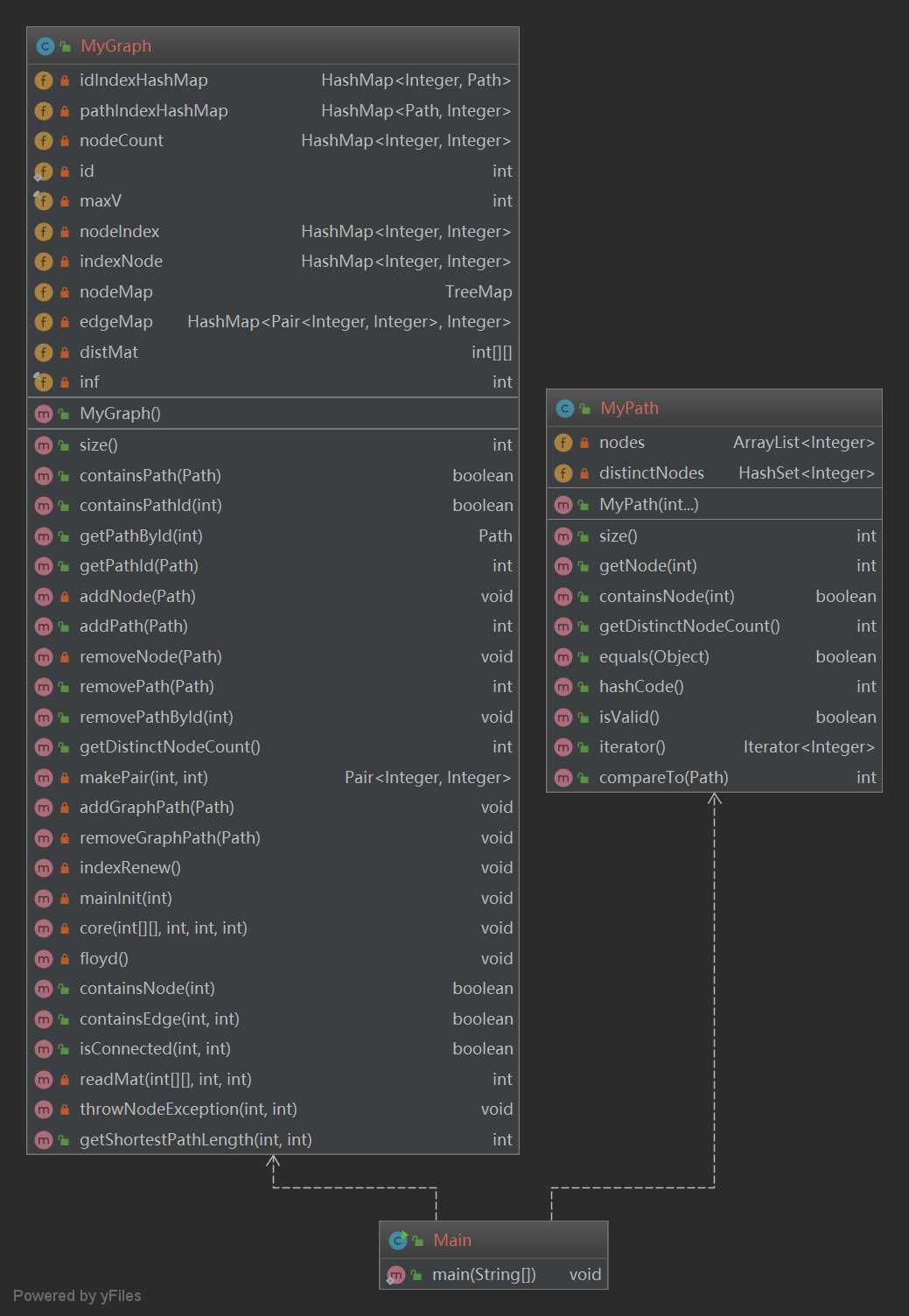
　　本次作业的任务是，实现容器类Path和数据结构类Graph。

　　Graph继承了上次的PathContainer接口，本应采用继承的机制，但由于继承对于父类中的私有成员的访问较麻烦，为了省事选择了复制粘贴 :-) 

　　对于Graph这个数据结构类，采用HashMap<Pair<Integer,Integer>, Integer>记录有边相连的节点及节点间边数；由于选取floyd算法进行最短路的计算，构建静态二维数组distMat记录节点间距离（于是架构很不美观），为此需要为节点编号与二维数组索引用HashMap（nodeIndex/indexNode）构建映射关系；需要注意的是由于增删路径导致节点的增删，每次增删路径都要为所有现存节点更新一次索引值，这里用nodeCount构造TreeMap按节点编号key升序排序，再重新构造索引映射的HashMap；每次增删路径更新完索引值后，调用一次floyd（）算法对距离矩阵进行更新，注意可以利用矩阵的对称性及现存不同节点个数对原始floyd算法进行常数优化（事实证明效果不错）。这样就把最短路等计算的时间复杂度分摊到本就无法降低复杂度的修改类方法中，使得大量查询类指令的复杂度大大降低。

• BUG分析

　　这次真的特别愚蠢，理解错了指导书对于同一时刻最多出现250个不同节点的描述，没有在增删路径时从头更新索引值而是不断让索引下标递增（其实也可以对0~255的索引值设置一个boolean数组标记是否已被使用，就不必从头更新），于是，当上千条指令总共出现过的不同节点超过255个时就会直接爆炸（数组越界异常）。只能说自己没考虑清楚，并且测试的数据量不够大，没能及时发现这个致命的bug。

　　互测时大多是WA类型错误，猜测是使用bfs或dij算法时出了问题（由于时间紧张并没有去读他人代码找逻辑漏洞）。

第十一次作业：简单地铁系统（RailwaySystem）

• 类图　　 

• 架构设计

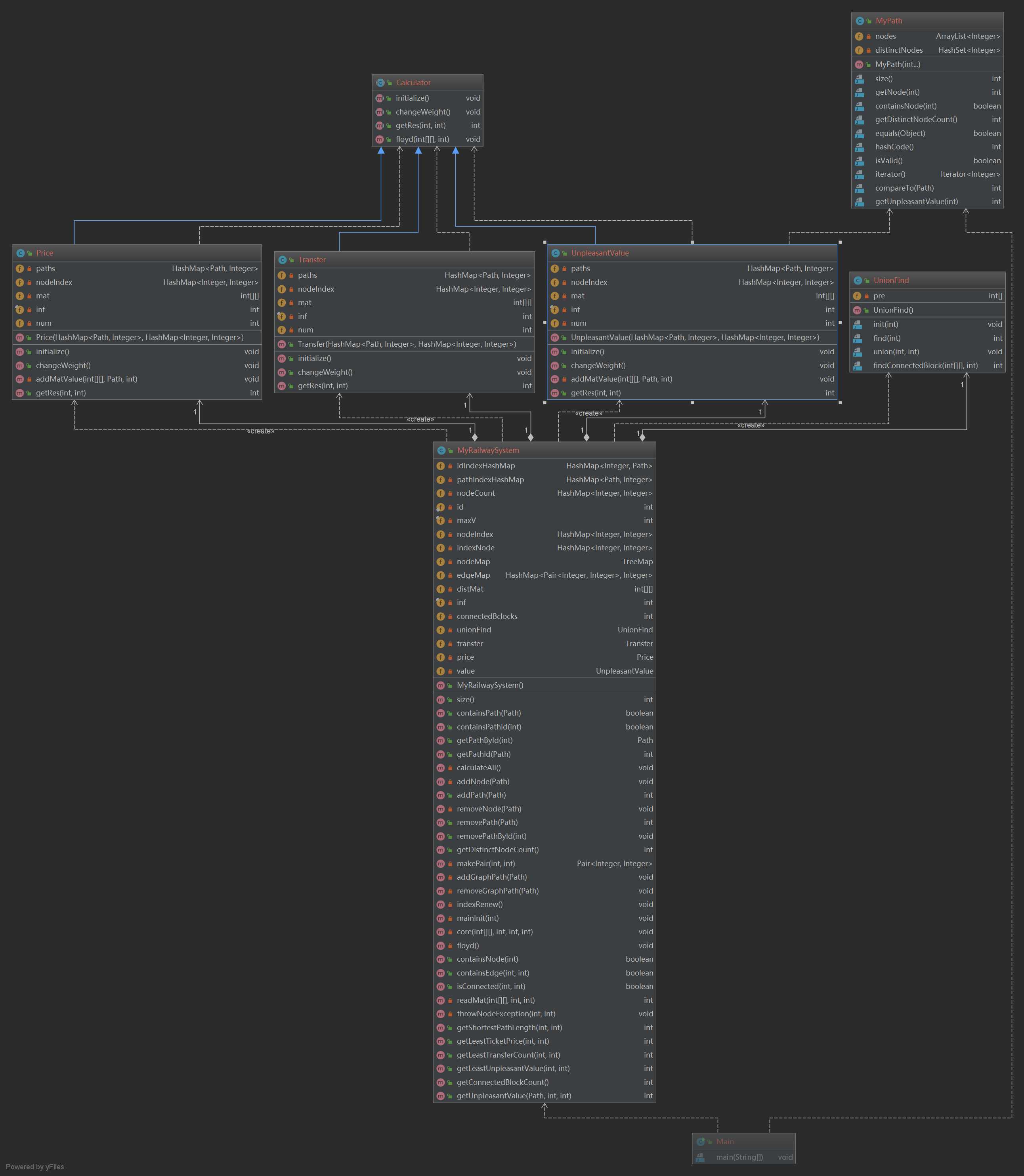
 　　本次作业的任务是，实现容器类Path和地铁系统类RailwaySystem。

　　 同理这次的RailwaySystem延续了上次Graph的所有功能（因此这一部分都没有修改），并在此基础上要求实现计算连通块个数、最少换乘次数、最少票价、最低不满意度的功能。其中换乘次数、票价、不满意度都可抽象成不同边权的问题，关键在于如何处理“换乘”；连通块个数的计算感觉比较孤立，就按查到的常用做法封装了一个并查集类做了。

　　关于如何处理换乘，由于不会拆点，就按讨论区dalao给出的“加边法”来了。把这三类计算单独开类封装，每次增删路径时，对每一条现存Path的各个节点进行节点间“最少”权值的计算（对每条Path应用floyd计算权值可以避免环路造成的一系列问题），并把节点间权值加入到相应的权值矩阵中，注意在权值矩阵应用floyd算法之前各个权值矩阵存储的就是路径中节点间的最小权值，因此出现在不同Path中的相同节点需要不断进行最小权值的更新，全部更新完再对权值矩阵进行floyd的计算。可以看出floyd应用在许多不同层次上，因此更好的做法应该是对floyd这一类计算单独开类封装。

• BUG分析 

　　败得最惨的一次，原因在于写代码之前没有把做法理清楚，对一条Path计算节点间最小权值时错误地采用了for循环顺序遍历，顺序遍历计算最小权值的后果就是一旦出现前溯环路就会计算出错。因此对每条Path应用floyd计算节点间最小权值才是正解。

一些心得体会

•  第一次接触JML，对于规格化设计与契约式编程有了初步的了解。
  • 最初对JML繁多的各种语法约束感到害怕，后来在接触的过程中逐渐加深理解，经过这一单元的训练，读懂那些规格已经不那么困难了。感觉对这种编程形式的好处体会得最深的应该还是这个单元的第一次作业，在理解了实现方法的规格后，按照自己的实现对方法进行填充，每个方法都写得十分精简，最多也才达到十几行，而且可读性极强（来自一个以往都要费尽心思把方法行数压缩在60行以内的人的感慨）。
  • 遗憾的是，从这个单元第二次作业开始，至少我个人就没有体会到JML规格带来的好处了。虽然我会去认真阅读并理解每一个方法的规格，但我并不觉得这对于最终完成作业有什么必要性，比如containsEdge和getShortestPathLength两个方法，在不阅读规格的情况下，我们也能知道这两个方法要求实现的功能；第三次作业给出了大篇幅的规格说明，出于训练的目的通篇看了下来，花了不少时间。说实话，虽然JML语言能保证逻辑的严密性，有时候是不是过于繁杂冗长了呢？至少那些方法我个人还是看指导书才真正理解的。同时，感觉这两次作业过于数据结构，至少个人是把重心都放在算法和数据结构上（当然也可能是因为wtcl）
  • 关于撰写规格，虽然经过这个单元的训练读懂规格已经不成难题，但个人感觉对于撰写规格还是一窍不通。我可以根据给出的方法规格去实现具体的方法；但在这个单元的作业中我从来没有为自己的方法撰写规格、再去实现，我相信绝大多数人都没有做过这件事，大家应该都是想到要实现一个什么功能去构造一个相应的方法，而不会花时间特意去撰写规格。我还是觉得"撰写规格"和"实现规格"不应该是同一个人去做的事情。

OO第三单元总结

标签：十分   无向图   索引下标   做了   接口   ros   boolean   映射   边界条件   

原文地址：https://www.cnblogs.com/Ace424/p/10901860.html