标签:思考 最短路径 满意度 表达式 单元测试 com 起点 ldo 图结构
JML是一种形式化的,面向JAVA的行为接口规格语言,它结合了Eiffel的契约方法和Larch方法,以及细化演算的一些元素,有着坚实的理论基础。
JML最主要的语法有前置条件,后置条件,不变式,通过这些语法对输入和输出进行约束,也就是达成了一种契约。当模块实现后,只要输入输出满足这些约束表达式就满足了规格的要求。JML主要使用java的语法,除此之外还有自己的一些语法,比如/forall,/exist等等,来实现对输入输出的约束。
JML拥有自己的一套工具链,其中最有用的是断言检查编译器jmlc,单元测试工具jmlunit以及jmldoc。另一种OpenJML可以通过命令行工具进行jml语法检查,可以说OpenJML是JML工具链的核心。
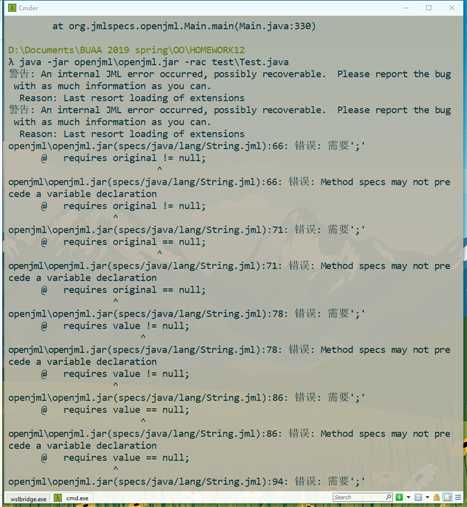
在下载openjml和jmlunitng之后,编译时发生以下错误,在多次尝试后无果
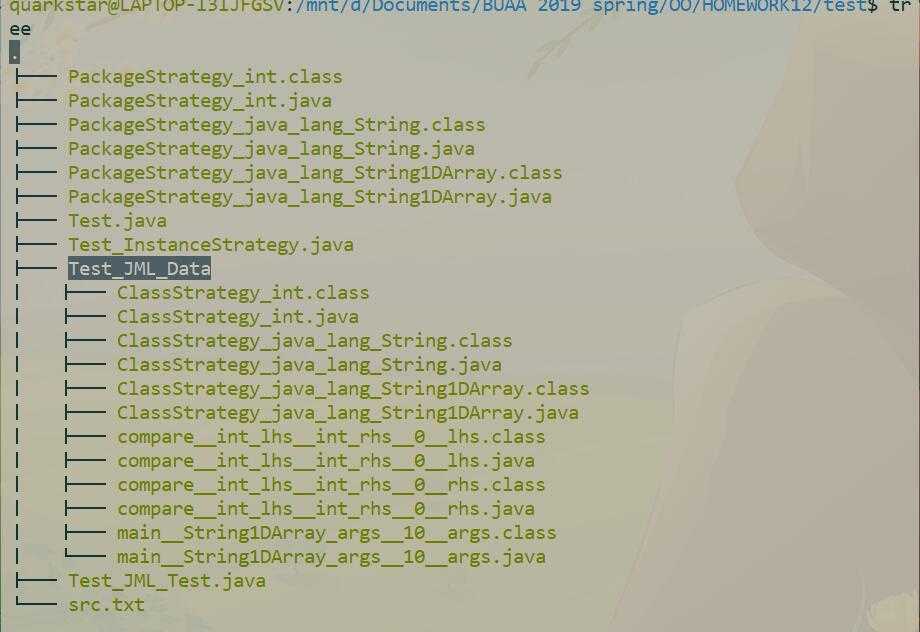
生成测试文件后文件结构如下
通过阅读他人博客,我发现jmlunitng还是有一定局限性的,它生成的测试用例多是边界数据,而且不能很好的符合requires的要求。
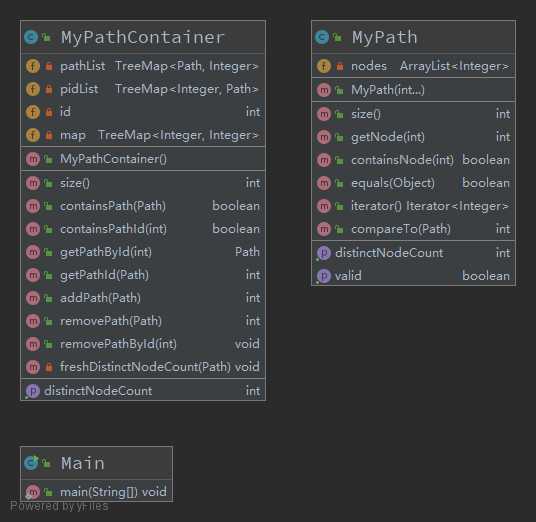
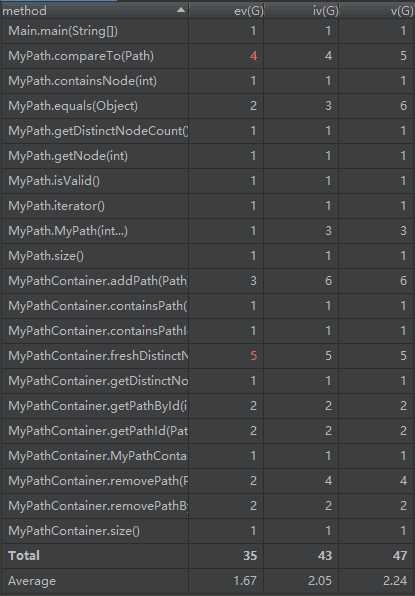
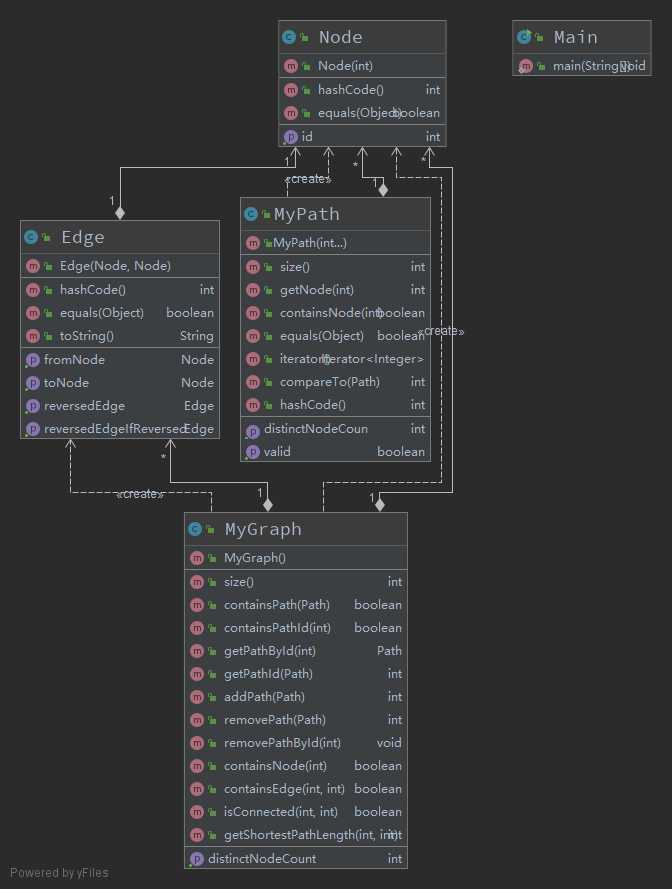
第一次作业比较简单,其中最困难的部分在于如何建立Path和PathId的双向映射,我才用了两个TreeMap,一个是TreeMap<Path, Integer>, 另一个是TreeMap<Integer, Path>,用空间复杂度减少时间复杂度。
在Distinct_Node_Count,我在每次addPath时就将此值计算好,调用时直接返回即可。
本次作业比较简单,我自己在强测和互测中都没有bug,也没能找出别人的bug。
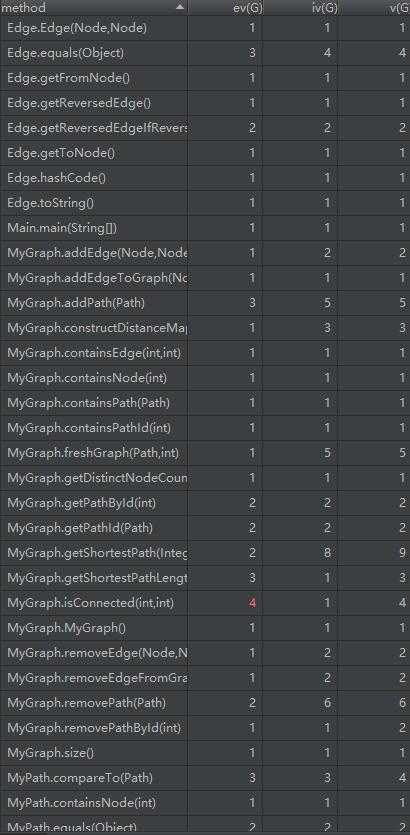
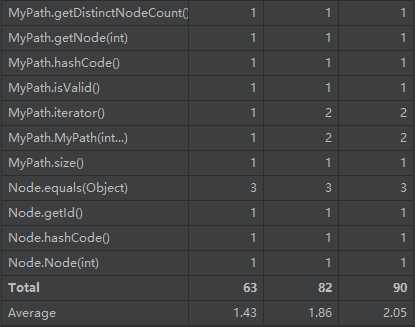
(由于作业提交的代码有点惨……这里使用bug修复后的作业)
这次修复后我将node和edge都提炼成了新的类,也就弃用了上次的代码。距离图也从HashMap<Integer, HashMap<Integer, Integer>>变为了HashMap<Edge, Integer>,不仅时简洁了很多,而且也简化了自己写代码时候的思维。图采用了邻接表的方式储存。
本次作业理论上应该继承上次的PathContainer,但是我的改动比较大,也就整体重写。由于图的结构变更指令比较少,我采用的策略是:每次图结构变更指令后重新构建图,然后将图当作静态图来处理。对于时间复杂度最高的最短路径,我采用了dijkstra算法,并在完成计算后记录“该点为起点的最短路径都已经计算”,将结果缓存下来,加快了计算。
本次作业在强侧部分出现了大面积TLE,而且不仅仅是最短路径搜索算法的问题。据我分析原因主要有两点:
最短路径搜索问题
求最短路径有三种方法,bfs、Floyd算法和Dijkstra算法。其中Floyd算法时间复杂度为o(n^3),运行一次就可以求出整张图上任意两点之间的最短路径,Dijkstra算法时间复杂度低,运行一次可以求出出发点到剩下所有点的最短路径。这两种算法的选择就在于图结构更改的次数。如果图结构更改很少而有大量的查询最短路径的指令,那么floyd算法会更有优势。但是如果图结构更改相对频繁,则Dijkstra算法更快。在本次作业的情形下还是使用Dijkstra算法更能符合题目的要求。
查询问题
在本次作业种包含了大量的查询指令,我在一开始完成作业时不知道remove指令,只会将值设为null,导致查询种出现了很多无谓的循环,我应该在此浪费了很多的时间。这也提醒我要对java语法多加了解,善于运用java种自带的数据结构。
寻找别人bug时我没有针对性查找,只是将自己的测试数据提交了上去。
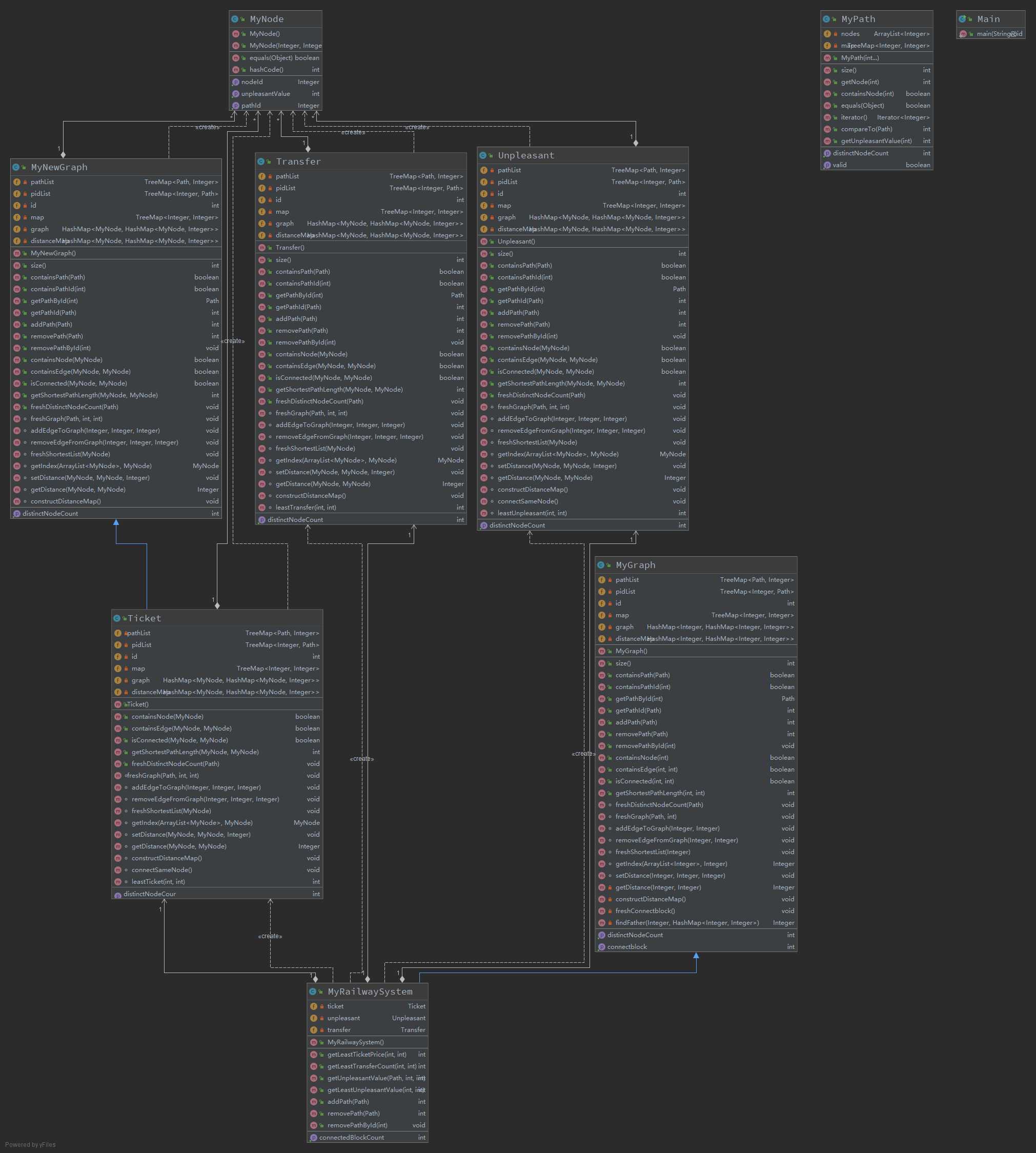
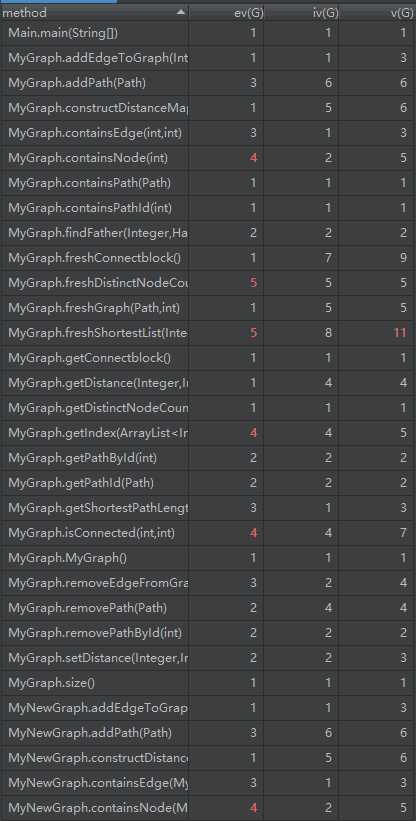
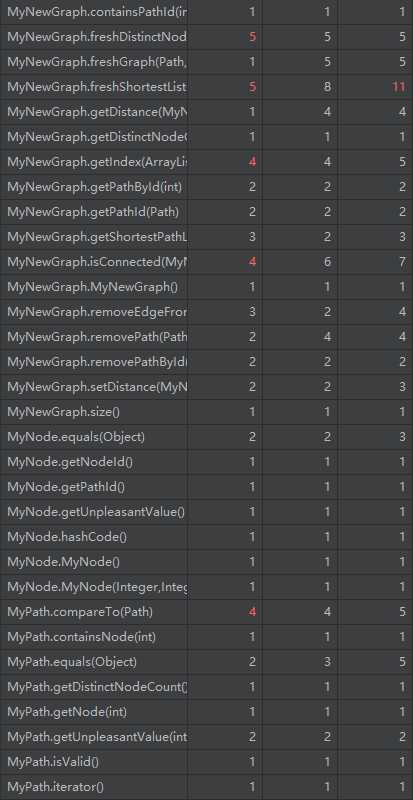
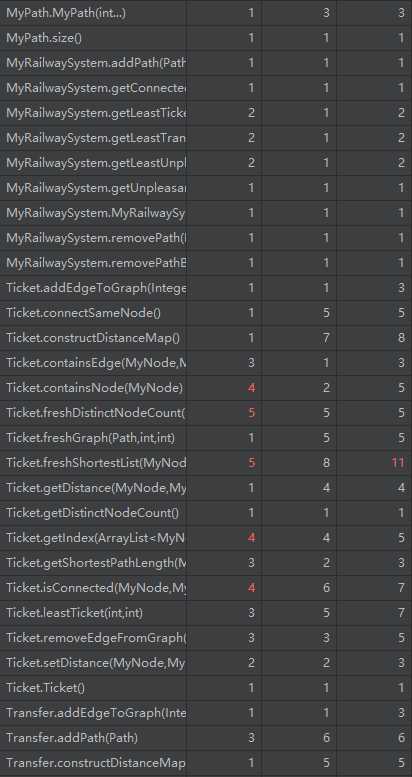
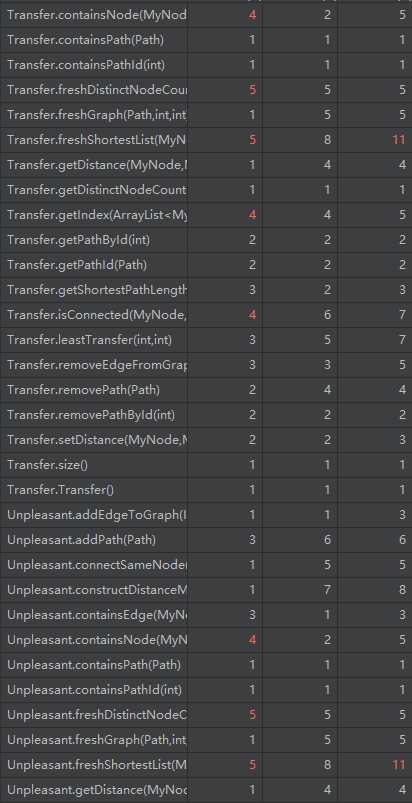
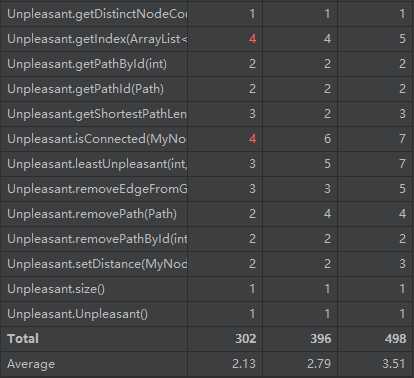
本次作业完成的很差……由于bug一直没有修复好,为了正确性我出现了大量的重复代码。
本次作业一共有四个问题,而不满意度,最少换乘和票价问题其实是同一个问题,只需要设置不同的边的权值。另一个图的联通块问题我采用了并查集,每次图结构变更之后重新计算。
不满意度,最少换乘和票价需要包含三个新的图,这三个图因为换乘的问题与第二次作业中的最短距离问题出现了一些不同。我采用的方法是将经过多个Path的Node拆分,但也在这里出现了新的问题。这一部分将在bug分析里具体描述。
本次作业最主要的问题还是TLE,由于星期日才知道上次作业的bug,并且发现第二次作业的bug不是修修补补就可以修改的,要整体性重写……于是第三次作业跟着一起炸了。除了第二次作业的问题外,我还想说一个拆点的问题:在我提交的作业中,一个Node如果在x个Path上,那么将它拆成x个不同的点。那么查询以它为起点的最短路径的时候,应该用哪个点作为起点呢?我原来的做法是将x个点都作为起点遍历一遍,执行了x次Dijkstra,显然时间复杂度爆炸了。评论区里有一个很好的方法:对每个Node拆成2+x个点,多出来的两个点一个作为起点,一个作为终点,每个地铁站的终点到起点连边的边权为y。每个站台往它所在的终点连边的边权为0,每个地铁站的起点往它的每个站台连边的边权为0。
在学习了一个月的规格后,我印象最深刻的就是老师告诉我们“思维的转变”。写规格就像是写说明书,只需要告诉别人这个黑箱是怎么用的。比如一个求解最短路径的模块,我们由一看到最短路径就想到“迪杰斯特拉”“弗洛伊德”转变为思考我们这个模块要接受什么样的数据进来,要输出什么样的结果出去。这种契约设计的思想,我觉得是将任务的进一步划分。之前自己写代码就将设计和实现混在一起,写的时候先都写上去,发现有哪种方法用的比较多再将他提取出来。而现在则是提前做好完整的规划,然后再将模块一个一个实现。这样子在实现一个模块的时候觉得轻松了很多,不用考虑或者说已经事先考虑好了它给整体带来的影响,只需要实现就好了。在最后测试的时候也方便了许多,验证我的每一块“积木”都是正确的,哪块“积木”坏了就从哪里找问题。整个过程都变得更加井然有序。
标签:思考 最短路径 满意度 表达式 单元测试 com 起点 ldo 图结构
原文地址:https://www.cnblogs.com/quarkstar/p/10908262.html