标签:机器学习 回归 大小 develop tps 复杂 ict 特征 问题
之前介绍的简单线性回归,就是一个回归模型,是一个可用于机器学习的模型。什么意思呢?就是模型的状态(参数集合)是可以进化的,只要合理训练它,模型就能取得更好的预测状态,所以说模型可用于机器学习。
要应用机器学习,一开始就要考虑选择一个良好的模型(分类模型或回归模型),想清楚了,这步是很重要的,如果你选择了一个不对口的模型,你可能花了半辈子的样本挑选与训练,也得不到一个好的模型状态,最终预测不到好的结果。但这里讲的不是怎么选择模型,而是想说,模型是怎么进化的,也就是训练的过程是怎么样的。
又是一些枯燥的内容,但是我也没有办法,难道枯燥就不去了解吗?或者你有更好的表达办法?
你可能已经想像到,训练会一直在调整模型的参数。是的,训练就是要强大,强大就是要固化出最好的参数集合,跟你全面锻炼身体一样,你体重多少?
为了更具体地理解训练的运行原理,可以参考以下这张图(图片源于:https://developers.google.com/machine-learning/crash-course/reducing-loss/an-iterative-approach):
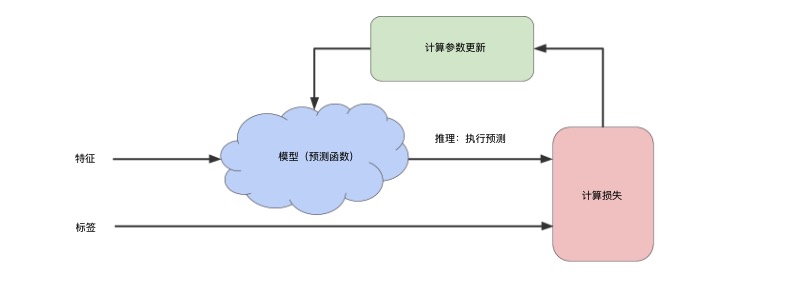
因为训练接受的样本是带标签的,所以交给模型的是特征与标签的组合,但你要注意,模型处理的是“所有”样本,它对“所有”样本进行预测,得到一堆预测标签,然后再计算误差或损失,然后再调整参数。所以你不要理解为一定是先处理一个样本就调参然后再来一个样本。这里,我留了一个后路,为了计算损失,并不一定要所有样本参与,甚至可以一次迭代只用一个样本,这个在最后再说。
比如,套用之前的简单线性回归模型,根据关系y=mx+b,每一个样本都得到预测标签。之后,根据预测标签与真实标签,进行损失计算,比如按均方误差计算出损失,如果损失已经很小了,或者若干次调整都不能让损失变小或变小的幅度很小,那你可以下结论了:这个就是最小损失,不用再训练了,模型的状态是最fit的了--这个叫训练收敛。
如果损失比上一次还小(还小很多)而且还不是你以为最小的值,那说明什么?说明还有好处可捞啊,还要调整参数以取得更小的损失啊。那调整参数之后,是不是预测效果就更好了呢?不知道!这时要对所有样本再预测一遍、再计算一次损失,才知道。于是,迭代开始了。
如此,反复迭代预测、算损失、调参的流程,至到天荒地老(即收敛,收敛了就放过它)。迭代的过程是自驱动的,这个是机器学习的特点。
迭代的流程是比较重要的概念(能让你较全局地理解机器学习),你有必要在脑海中多想一下这个情景,为了配合你,小程把一元回归模型的图放在下面,你想像一下,图里面的那根线,调整一个角度后,对所有点算一次损失,如果不是最小损失,就再调整一个角度...

上面多次说到调整参数,说得轻巧,怎么调整?随便加1或减1吗?
在迭代学习的过程中,机器会自驱动地调整模型的参数。调整模型的参数是机器学习的一个重要环节,那么,如何调整模型的参数呢?
以简单的一元回归(是一块钱回到家的意思吗?)为例:y=wx+b,要调整的参数就是w跟b,怎么调?首先你要记得你的目的,你调参的目的,是为了得到最小损失,那w跟b是何值时,才是最小损失呢?
先说一个不经过设计的自然的想法,假设先调整w(b先随便固定一个值),如果我能把所有的w值的损失都计算出来了,也就是对于w取{1,-1,2,2.5,...}各个值时,都算出所有点的整体损失,那不是有最小损失了吗?最小损失对应的那个w值就是最佳的参数啊。
想法是没错的,但是,一般来说,越自然的想法,越不是一个好的算法。
算法就是设计的东西。怎么调整出最佳参数,同样有更好的算法,而不是对所有w值全量计算(效率太低了!),其中一个常用算法叫梯度下降法。
首先要理解一个前提。据研究(不是我的研究),损失跟权重的关系,是一个碗状图(这就是损失函数),就是这个:
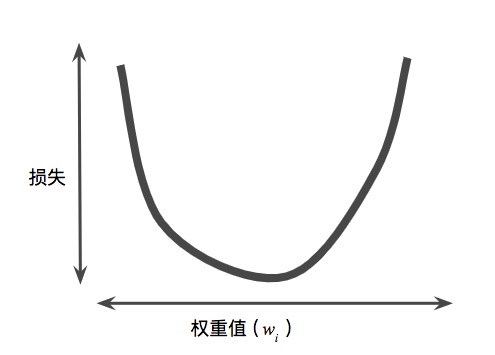
有什么特点?一个特点是,有一个最低点,就是损失最小的点,这个就是我们的目标(对应的w值就是最佳参数),另一个特点是,沿着碗边走,只要方向对而且移动幅度足够小,就一定能到达最低点。
要到达远方,现在就要出发。这里有两个关键点,一个是方向,一个是移动幅度。
怎么确定方向呢?比如对于曲线,往左还是往右(即w是增加还是减小),对于曲面呢?
这时,梯度下降法来帮你,它可以有效地去到最低点。
以下分隔线内的东西,横空而来,你若有兴趣则读一读,它告诉你,什么是梯度。
什么是导数?
导数是函数的导数,函数只有一个自变量时叫导数(否则叫偏导数)。直观点,函数都是曲线,所以导数就是曲线上某一点的导数(不说不可导的情况)。
某一点的导数是什么意思呢,就是这一点的变化率,定义大概是这样的(数学符号不好写):在某一点,在x的增量趋于0时,也就是x的变化很小很小很小时,y的增量与x的增量的比值,就是变化率。明显,以x的增量趋于0来描述了这一点的变化(让变化很小)。这个就是变化率的含义,简单来说,导数就是变化率,描述了变化的情况。
换一个角度来说(只考虑变量值是实数的情况),先看看我的手绘图(你给多少分?):
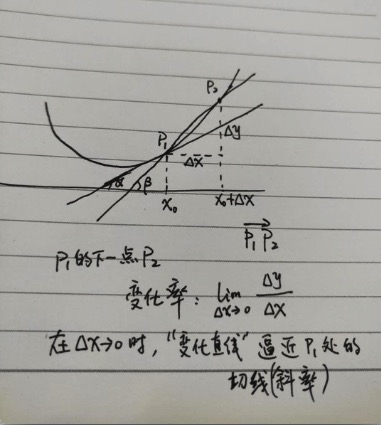
上图,表达的是p1下一步(“附近”)的变化率,为了好画线,找了一个很远的p2点。你可以想象,当p1的下一步变化很小很小时(dx趋于0时),p2就会无限接近p1,而这个过程,直线p1p2的变化是怎么样的?想象一下,是不是p1p2会越来越像p1处的切线?
点p1的导数,从另一个角度来说,就是这个地方的切线斜率。可以想象,如果曲线上的所有点,都取它的切线,就可以逼近曲线。这种用导数来还原曲线(函数)的办法,就叫积分。求导跟积分是互逆过程。
如果你还是不太明白,那知道一个概念就算了:变化、导数跟切线,是关联的东西。
什么是偏导数?
上面提到的损失函数是一个曲线,因为只有一个特征变量。如果有多个特征,那损失函数就不再是曲线,而是曲面(某点的切线有无数条)。曲面(多个自变量)时,不再叫导数,而叫某某变量的偏导数,只是为了明确是谁的变化率。而问题也在这里,为了得到x的偏导数,就要固定其它自变量,而此时的偏导数就只是沿x方向的变化(不能同时考虑进其它方向),这样就没有任意方向了,没有任意方向是个问题吗?
举个例子,假设你在山坡上,你要走到山谷的小湖中。如果每次移动你只能在x、y或z(平面与高度)中的一个方向移动(假设你总能移动哪怕是穿透),那你只能是“直上直下”、“直前直后”的,这个不是高效的走法。此时,为了形象,手绘图再次出场:
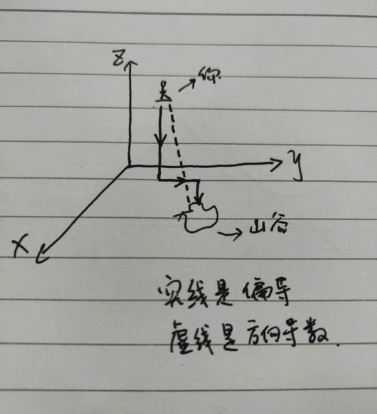
图中的虚线(实际上有无线),可能让你更快地到达小湖洗脚,这个叫方向导数。
什么是方向导数?
为了解决直前直后的偏导数的问题,引入另一个概念就是方向导数。方向导数就是任意方向的导数,可以想象,你所在的山坡的位置,有无数的方向导数,于是,哪一个方向导数(也就是变化率)是变化最大的?变化最大的方向在哪里?这个大小跟方向都是可以求出来的。
为了标志方向导数的最大值跟方向,引入了一个名字,叫梯度。
什么是梯度
终于到我出场了,梯度是一个矢量(有大小跟方向),梯度的值就是最大的变化率(方向导数的最大值),梯度的方向就是最大变化率的方向(取得最大方向导数的方向)。
所以,沿着梯度的反方向,就是下降最快的方向,就是最快到损失最低点的方向,而梯度下降算法就利用了这个特征。
梯度是一个矢量,值是最大方向导数的值,方向是取得最大方向导数的方向。是不是很绕?是的,跟废话一样绕。简单来说,梯度的反方向代表着最佳的前进方向,指引你快速到达损失最低点。
问题是,我不会计算梯度啊,怎么办?在应用的世界,这都不是问题,比如tensorflow会帮你计算梯度,你躺着就好。
但稍微理解一下操作总是要的吧。梯度下降法,在整体操作上,还是较容易理解的。可以参考这个图(图片来源于:https://developers.google.com/machine-learning/crash-course/reducing-loss/gradient-descent):
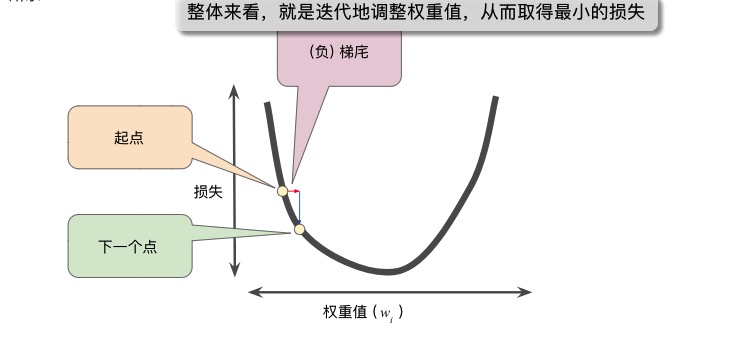
前面提过,走到最低点,一看方向,二看移动幅度。方向的问题用梯度解决了,那移动的幅度呢?这时引入一个概念,叫学习速率(learning_rate),也叫步长。移动的幅度,就是当前点的梯度值乘以学习速率(比如是0.001),再加上原梯度值。
如果学习速率很小,那总会走到损失的最低点,但训练时间有可能很长。如果学习速率很大,那有可能总是跳过最低点而无法收敛(注意,不是说一出现跳过最低点就一定不能收敛,它可以左右摆动最终到达最低点,因为移动幅度是变化的,跟陡峭的程度有关)。
一般可以边训练边观察,寻找一个折中的学习速率值,这个跟样本的数量、特征复杂度等有关。对于学习速率的直观感受,你可以在这个页面操作一下:
https://developers.google.com/machine-learning/crash-course/fitter/graph
以上就介绍了怎么调整参数。
最后,再重提一下损失曲线,上面说每一次迭代都要对所有样本预测并计算损失,而实际上,“所有”并不是终极方案,如果有更优的方案呢,如果不必所有的样本都计算一次呢(毕竟有时样本是海量的)?这时,一些优化方案就出来了,比如随机梯度下降(只使用一个样本)、小批量随机梯度下降(多一点样本),这些就不细说了,谁用谁研究。
总结一下,本文介绍了模型训练的迭代学习的原理。迭代学习的过程,主要是模型的计算参数被调整,进而触发反复的标签预测(预测是为了算损失)、损失计算与模型参数调整,是一个自驱动的过程。在迭代的过程中,调整模型的参数是重要的一环,梯度下降算法可以有效地调整模型参数,以达到最小的损失,从而使训练收敛。

标签:机器学习 回归 大小 develop tps 复杂 ict 特征 问题
原文地址:https://www.cnblogs.com/freeself/p/10919610.html