标签:相同 实例 不同的 价值 方向 bsp 需要 平面 code
降维
降维的动力来自于维度魔咒,动辄几万个甚至更多的特征会导致训练变慢,而且,维数越高越难找到合适的解决方案。特征的维数对应着相同维度的一个高维空间,高维空间中点与点的距离很容易变得很大,也就是实例之间的距离很大,训练集的特征空间很稀疏,这容易导致过拟合,当然,通过添加足够多的训练实例,在理论上可以解决这个问题,然而,这个方法需要增加的实例数是成指数增长的,因此不好用。人们于是转而寻求其他的方法:降维。
降维之所以可行,基于两点:1.某些特征重要性很低,忽略它也不会对结果造成很大的影响;2.某些特征之间有某些联系,可以通过这些联系来简化特征。
降维对于可视化也是有好处的,通过降低维度,然后可视化,可能得到一些有价值的洞见。
PCA
有很多降维方法可以用,比如投影。PCA也是一种投影方法,它的关键在于找到一个最接近数据的超平面,然后投影其上。
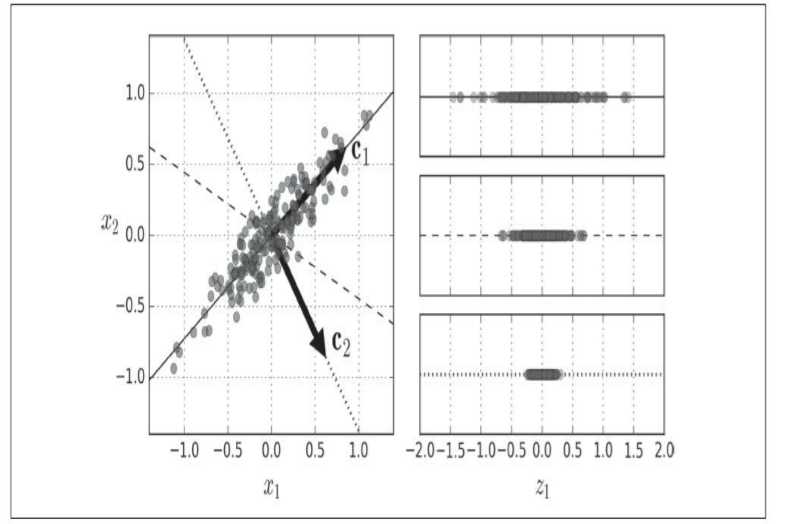
上面将二维数据沿三条不同的轴进行映射,可以看到第一条轴上保留了最大的差异性,而第三条轴只保留了很小的差异性。它的实质是使得原始数据和投影后的数据的均方距离最小。
主成分
PCA方法可以识别出训练集中哪条轴对差异性的贡献最大,这些轴的数量与特征维数相同,相互垂直。第i条轴的单位向量就是第i个主成分。主成分的方向是不稳定的,如果数据被打乱,主成分的方向也发生变化,不过一般它们形成的超平面是不变的。得到主成分的数学方法是矩阵的奇异值分解。
方差解释率表示每个主成分轴对数据的方差的贡献率。它可以作为选择要降低的维数的依据。将主成分方差解释率依次相加,当贡献率足够大时,对应的维数就是应当选择的维数。
用PCA压缩后还可以进行解压,当然它不可能完全还原。
标签:相同 实例 不同的 价值 方向 bsp 需要 平面 code
原文地址:https://www.cnblogs.com/gadflyWZQ/p/10920702.html