标签:http else nbsp return 最大的 public int 最大 状态转移方程
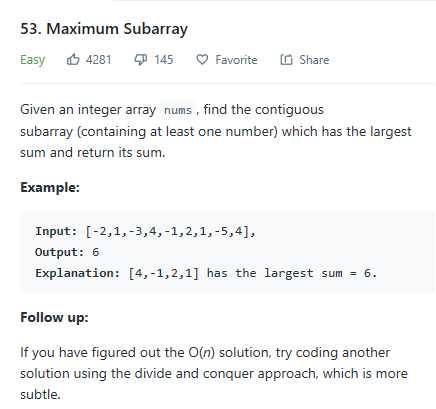
题意:寻找子数组的和最大。
思路:设置dp数组来保存到第i位的最大和。
判断第i-1位的正负,若dp[i-1]<0 则 dp[i] = nums[i]; 若 dp[i-1] > 0 则 dp[i] = dp[i-1] +nums[i];
最后用 max_num = max(max_num, dp[i]); 来存储最大的和。
class Solution { public: int maxSubArray(vector<int>& nums) { int len = nums.size(); if(len == 0) return 0; if(len == 1) return nums[0]; vector<int> dp(len, 0); //dp[i]: 以第i个元素为结尾的最大子序列和 dp[0] = nums[0]; int max_num = dp[0]; for(int i=1; i<len; i++){ if(dp[i-1] > 0) dp[i] = dp[i-1] +nums[i]; else dp[i] = nums[i]; } return max_num; } };

题意:求子数组(数组里的数是连续)的最大乘积。
思路:因为数组里有负号,所以用两个数组dp_max 和 dp_min 分别保存到当前位置i的最大值和最小值。
状态转移方程:
dp_max[i%2] = max( max(dp_max[(i-1)%2]*nums[i], nums[i]), dp_min[(i-1)%2]*nums[i]);
dp_min[i%2] = min(min(dp_min[(i-1)%2]*nums[i], nums[i]), dp_max[(i-1)%2]*nums[i]);
class Solution { public: int maxProduct(vector<int>& nums) { int n = nums.size(); if(n==0) return 0; int dp_max[2]={nums[0], 0}, dp_min[2]={nums[0], 0} ; int ans = nums[0]; for(int i=1; i<n; i++){ dp_max[i%2] = max( max(dp_max[(i-1)%2]*nums[i], nums[i]), dp_min[(i-1)%2]*nums[i]); dp_min[i%2] = min(min(dp_min[(i-1)%2]*nums[i], nums[i]), dp_max[(i-1)%2]*nums[i]); ans = max(ans, dp_max[i%2]); } return ans; } };
标签:http else nbsp return 最大的 public int 最大 状态转移方程
原文地址:https://www.cnblogs.com/Bella2017/p/10957868.html