标签:int info code 导数 gradient src 好的 oba glob
学习率 learning_rate:表示了每次参数更新的幅度大小。学习率过大,会导致待优化的参数在最 小值附近波动,不收敛;学习率过小,会导致待优化的参数收敛缓慢。
在训练过程中,参数的更新向着损失函数梯度下降的方向。
参数的更新公式为: ????+?? = ???? − ????????????????_??????????
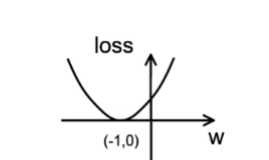
假设损失函数为 loss = (w + 1)2。梯度是损失函数 loss 的导数为 ∇=2w+2。如参数初值为 5,学习
率为 0.2,则参数和损失函数更新如下:
1 次 参数 w:5 5 - 0.2 * (2 * 5 + 2) = 2.6
2 次 参数 w:2.6 2.6 - 0.2 * (2 * 2.6 + 2) = 1.16
3 次 参数 w:1.16 1.16 – 0.2 * (2 * 1.16 + 2) = 0.296
4 次 参数 w:0.296
代码如下:
#coding:utf-8 #设损失函数 loss=(w+1)^2, 令w初值是常数5。反向传播就是求最优w,即求最小loss对应的w值 import tensorflow as tf #定义待优化参数w初值赋5 w = tf.Variable(tf.constant(5, dtype=tf.float32)) #定义损失函数loss loss = tf.square(w+1)#tf.square()是对a里的每一个元素求平方 #定义反向传播方法 train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss) #生成会话,训练40轮 with tf.Session() as sess: init_op=tf.global_variables_initializer()#初始化 sess.run(init_op)#初始化 for i in range(40):#训练40轮 sess.run(train_step)#训练 w_val = sess.run(w)#权重 loss_val = sess.run(loss)#损失函数 print "After %s steps: w is %f, loss is %f." % (i, w_val,loss_val)#打印
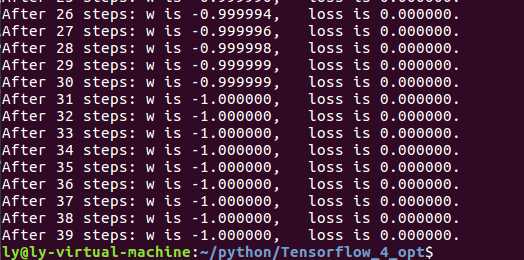
有结果可以很好的反映出w=-1;
学习率过大,会导致待优化的参数在最小值附近波动,不收敛;学习率过小,会导致待优化的参数收
敛缓慢。
例如:
① 对于上例的损失函数 loss = (w + 1)2。则将上述代码中学习率修改为 1,其余内容不变。
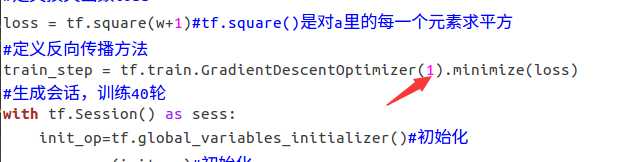
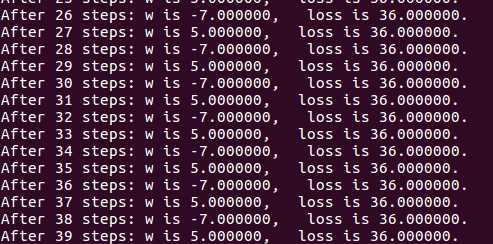
② 对于上例的损失函数 loss = (w + 1)2。则将上述代码中学习率修改为 0.0001,其余内容不变。 实验结果如下:
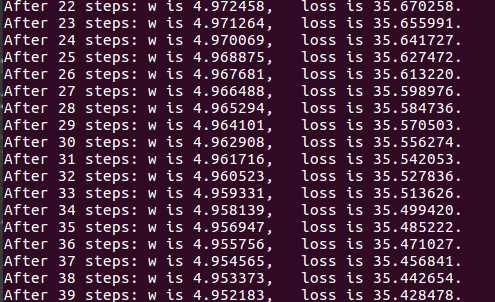
实验结果符号我们的预期学习率过大,会导致待优化的参数在最小值附近波动,不收敛;学习率过小,会导致待优化的参数收敛缓慢。
标签:int info code 导数 gradient src 好的 oba glob
原文地址:https://www.cnblogs.com/fcfc940503/p/10960936.html