标签：存储 算法 other 探测 复杂 turn 分析法 arch while
本章学习了关于查找的算法知识。
查找算法的评价指标：关键字的平均查找长度ASL。
查找成功的平均查找长度：
不成功查找算法：若查找概率相同且进行顺序查找，每次查找都不成功 ASL=n
（1）顺序查找：
【传统】
1 find(SSTable s, KeyType x） 2 { 3 int i; 4 for(i=0;i<=s.length;++i) 5 if(x==s.R.[i].key) 6 return i; 7 return 0; 8 }
特点：<1>时间复杂度为O(n)
<2>比较次数为2n
（返回值可以是key关键字的下标，也可以直接返回数据）
【哨兵查找】
1 find(SSTable s;KeyType x) 2 { 3 int i; //辅助空间，与n无关 4 s.R[0].key=x; //待查找的值放在0号下标 5 for(i=s.length;x!=s.R[i].key;--i); 6 //查找到的情况i介于1~n之间；找不到i=0 7 //当当前关键字与x不同时，x往前推 8 return i; 9 }
特点：<1>时间复杂度为O(n)
<2>比较次数为n
（2）折半查找（又称二分查找）
1 //待查找数字时有序的（前提） 2 int find(int a[], int n, int x) 3 { //在a[1:n]中查找值为x的元素，返回其下标或0 4 int l=1,r=n,mid; 5 while(l<=r){ 6 mid=(l+r)/2; 7 if(x==a[mid]) return mid; 8 if(x>a[mid]) l=mid+1; 9 else r=mid-1; 10 } 11 return 0; 12 }
特点：<1>T(n)=O[log2n]
<2>S(n)=O(1)
若对数组进行二分查找，则时间复杂度为：O(nlog2n)
数组不一定有序，T(n)=O(nlog2n)+O(log2n)=O(nlog2n)
二分查找适用于静态查找，不适用于数据量大的查找（超过内存可用存储空间）
2.树表的查找：
(1)二叉排序树的二叉链表存储表示
1 typedef struct 2 { 3 KeyType key; 4 InfoType otherinfo; 5 }ElemType; 6 typedef struct BSTNode 7 { 8 ElemType data; 9 struct BSTNode *lchild, *rchild; 10 }BSTNode *BSTree;
(2)二叉排序树的递归查找
1 BSTNode* search(BSTree t, KeyType x) 2 { 3 if(t==NULL) return NULL; //为空树的情况表示找不到 4 if(t->data.key==x) return t; //非空，且根结点的值为关键字 5 if(t->data.key>x) 6 return search(t->lchild,x); //返回 7 else return search(t->rchild,x); 8 }
(3)二叉排序树的插入
1 void InsertBST(BSTree &t, ElemType e) 2 { 3 if(t==NULL){ 4 s=new BSTNode; 5 s->data=e; 6 s->lchild=s->rchild=NULL; 7 t=s; 8 } 9 else if(e.key<t->data.key) 10 InsertBST(t->lchild,e); 11 else if(e.key>t->data.key) 12 InsertBST(t->rchild,e); 13 }
建立的过程就是要不断进行动态查找
(4)平衡二叉树
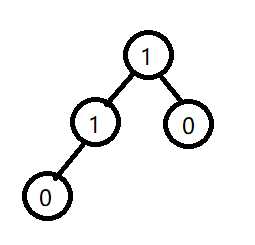平衡二叉树上所有结点的平衡因子只能是1，-1，0.
(5)B-树 B+树
B+树：实现B-树的全部功能，同时增加了区间查找。
3.散列表的查找：
存储结构是一个数组
构造散列函数的几种常用方法：
（1）数字分析法
（2）平方取中法
（3）折叠法
（4）除留余数法
<1>开放地址法
【1】线性探测法
若查找过程中遇到某一单位为空，则判断为找不到。
【2】二次探测法
【3】伪随机探测法
造表时要把序列记录下来，查找也要以同样序列查找
<2>链地址法
本章的学习思路较为清晰，希望下周能好好学好新章节内容，同时花多点时间开始进行复习，多进行实践。
标签：存储 算法 other 探测 复杂 turn 分析法 arch while
原文地址：https://www.cnblogs.com/pppipio/p/10965075.html
