标签:lam color 说明 -o seo 设计 严格 公式 个性
如果\(f\)可分为俩个变量:\(f(x, y)=\varphi(x) + \psi(y)\), 于是:

如果\(f\)是完全可分的,即\(f(x) = \sum_{i=1}^n f_i (x_i)\):
\[
(\mathbf{prox}_f(v))_i = \mathbf{prox}_{f_i}(v_i)
\]
这个性质在并行算法的设计中非常有用。
如果\(f(x) = \alpha \varphi (x) + b\), \(\alpha > 0\):
\[
\mathbf{prox}_{\lambda f} (v) = \mathbf{prox}_{\alpha \lambda \varphi} (v)
\]
如果\(f(x) = \varphi (\alpha x +b)\), \(\alpha \ne 0\):
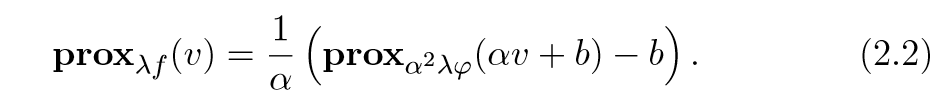
证:
\[
\begin{array}{ll}
\mathbf{prox}_{\lambda f}(v) &= \mathrm{argmin}_x \varphi(\alpha x+b) +\frac{1}{2\lambda}\|x-v\|_2^2 \&= \mathrm{argmin}_x \varphi(z) + \frac{1}{2\lambda}\|(z-b)/\alpha -v\|_2^2 \&= \mathrm{argmin}_x \varphi(z) + \frac{1}{2\lambda \alpha^2}\|z-b -\alpha v\|_2^2 \&= \frac{1}{\alpha} (\mathbf{prox}_{\alpha^2 \lambda \varphi}(\alpha v + b) - b)
\end{array}
\]
其中\(z=\alpha x+b\),证毕.
如果\(f(x) = \varphi(Qx)\),且\(Q\)为正交矩阵:
\[
\mathbf{prox}_{\lambda f} (v) = Q^T \mathbf{prox}_{\lambda \varphi}(Qv)
\]
如果\(f(x) = \varphi(x) + a^Tx + b\),则:
\[
\mathbf{prox}_{\lambda f}(v) = \mathbf{prox}_{\lambda \varphi} (v-\lambda a)
\]
证:
\[
\begin{array}{ll}
\mathbf{prox}_{\lambda f}(v) &= \mathrm{argmin}_x \varphi (x) + a^Tx + b + \frac{1}{2\lambda} \|x-v\|_2^2 \&= \mathrm{argmin}_x \varphi(x) +\frac{1}{2 \lambda} (x^Tx -2v^Tx+2\lambda a^Tx)+c \&= \mathrm{argmin}_x \varphi(x) + \frac{1}{2 \lambda} \|x-(v-\lambda a)\|_2^2 \&= \mathbf{prox}_{\lambda \varphi}(v-\lambda a)
\end{array}
\]
其中\(c\)为与\(x\)无关的项.
如果\(f(x) = \varphi(x) + (\rho/2) \|x -a \|_2^2\), 则:
\[
\mathbf{prox}_{\lambda f} (v) = \mathbf{prox}_{\widetilde{\lambda}\varphi}\big((\widetilde{\lambda}/\lambda)v + (\rho \widetilde{\lambda})a \big)
\]
其中\(\widetilde{\lambda} = \lambda / (1+\lambda \rho)\),证明方法和上面是类似的,重新组合二次项就可以了.
点\(x^*\)最小化\(f\)当且仅当:
\[
x^* = \mathbf{prox}_f (x^*)
\]
这说明,\(x^*\)是\(\mathbf{prox}_f\)的一个不动点,这个性质对于\(\lambda f\)也是成立的.

压缩映射的定义:
考虑映射\(T: (X, \rho) \rightarrow (X, \rho)\). 如果存在\(0 < a < 1\)使得对任意的\(x, y \in X\)有:
\[
\rho (Tx, Ty) < a \rho(x, y)
\]
则称函数\(T\)是\((X, \rho)\)到自身的压缩映射.
如果\(\mathbf{prox}_f\)是一个压缩映射,那么显然,如果我们想要找出最小化\(f\)的\(x^*\),可以用下式迭代:
\[
x^{n+1} = \mathbf{prox}_f(x^n) \rightarrow x^*
\]
比如\(\mathbf{prox}_f\)满足\(L<1\)的Lipschitz条件.
近端算子有这个性质:

这儿有关于这块内容的讨论.
\(x = \mathbf{prox}_f(v) \Leftrightarrow v-x \in \partial f(x)\),其中\(\partial\)表示次梯度.
设\(u_1 = \mathbf{prox}_f(x), u_2 = \mathbf{prox}_f(y)\),则:
\[
x - u_1 \in \partial f(u_1) \y - u_2 \in \partial f(u_2)
\]
因为\(f\)是凸函数,所以\(\partial f\)是单调增函数:
\[
<x - u_1 - (y-u_2), u_1-u_2> \ge 0 \\Rightarrow \|u_1 - u_2\|_2^2 \le (x-y)^T(u_1-u_2)
\]
上面的单调增函数,翻译的估计不对,主要是我对这方面的只是也不了解,原文用的是monotone mapping, 我们来看凸函数\(f(x)\):
\[
f(y) \ge f(x) + \partial f(x)^T (y-x) \f(x) \ge f(y) + \partial f(y)^T(x-y)
\]
相加即得:
\[
(\partial f(x) - \partial f(y))^T (x-y) \ge 0
\]
还有严格凸的情况下有个特殊情况,这个怎么证明啊...而且,似乎在不是严格凸的,利用上面的迭代公式也是能够收敛到不动点的,可似乎不满足不动点定理啊.
而且作者将这个与平均算子(averaged operators)联系起来:
\[
T = (1-\alpha)I+\alpha N, \alpha \in (0, 1)
\]
以及迭代公式:
\[
x^{k+1}:=(1-\alpha ) x^k + \alpha N
\]
有以下事实成立:

以下的证明是属于

沿用其符号,令(注意是\(\inf\)不是\(\mathrm{argmin}\))
\[
f_{\mu}(x) = \inf_y \{f(y) + \frac{1}{\mu} \|x-y\|_2^2\}
\]
我们可以其改写为:

注意\(-\sup A=\inf -A\)
假设\(f\)是凸函数且可微的,那么:
\[
f^*(y)={x^*}^T \nabla f(x^*) - f(x^*)
\]
其中,\(x\)满足:\(y=\nabla f(x^*)\)。于是(注意\(\nabla f(x^*)=y\), 且上式是关于\(y\)求导):
\[
\nabla f^* (y) = x^*
\]
这就是\(\nabla f_{\mu} (x)\)的由来.
我们再来看其对偶表示:

其拉格朗日对偶表示为:

如果满足强对偶条件:
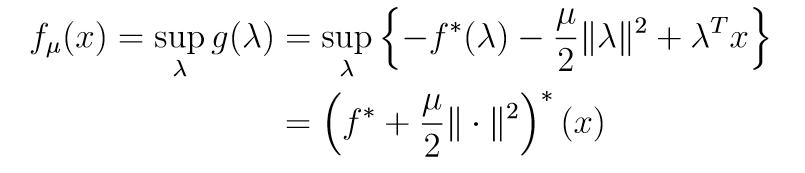
所以:
\[
f_{\mu}(x) = \frac{1}{2 \mu} \|x\|^2-\frac{1}{\mu}(\mu f+\frac{1}{2}\|\cdot\|^2)^*(x) =(f^* + \frac{\mu}{2} \|\cdot\|^2)^*(x) \\Rightarrow \frac{1}{2}\|x\|^2= ( \mu f + \frac{1}{2}\|\cdot\|^2)^*(x)+\mu (f^*+\frac{\mu}{2}\|\cdot\|^2)^*(x) \\Rightarrow x= \mathbf{prox}_{\mu f}(x) + \mu\mathbf{prox}_{\frac{1}{\mu}f^*}(\frac{x}{\mu})=x = \mathbf{prox}_{\mu f}(x) + \mathbf{prox}_{(\mu f)^*}(x)
\]
最后一步的结果通过对上式俩边求导得到的,不知道对不对,但是\(\mu=1\)的时候,下式是一定成立的:
\[
x = \mathbf{prox}_f(x) + \mathbf{prox}_{f^*}(x)
\]
Proximal Algorithms 2 Properties
标签:lam color 说明 -o seo 设计 严格 公式 个性
原文地址:https://www.cnblogs.com/MTandHJ/p/10990368.html