标签:资料 detail nbsp 输出 font 情况 大于 info 提升
kmeans 中k值一直是个令人头疼的问题,这里提出几种优化策略。
核心思想
1. 肉眼评价聚类好坏是看每类样本是否紧凑,称之为聚合程度;
2. 类别数越大,样本划分越精细,聚合程度越高,当类别数为样本数时,一个样本一个类,聚合程度最高;
3. 当k小于真实类别数时,随着k的增大,聚合程度显著提高,当k大于真实类别数时,随着k的增大,聚合程度缓慢提升;
4. 大幅提升与缓慢提升的临界是个肘点;
5. 评价聚合程度的数学指标类似 mse,均方差,是每个类别的样本与该类中心的距离平方和比上样本数;
示例代码
import numpy as np import matplotlib.pyplot as plt from matplotlib.font_manager import FontProperties from sklearn.cluster import KMeans from scipy.spatial.distance import cdist # 1 数据可视化 cluster1 = np.random.uniform(0.5, 1.5, (2, 10)) cluster2 = np.random.uniform(3.5, 4.5, (2, 10)) X = np.hstack((cluster1, cluster2)).T plt.figure() plt.axis([0, 5, 0, 5]) plt.grid(True) plt.plot(X[:, 0], X[:, 1], ‘k.‘) plt.show() # 2 肘部法求最佳K值 K = range(1, 10) mean_distortions = [] for k in K: kmeans = KMeans(n_clusters=k) kmeans.fit(X) mean_distortions.append( sum( np.min( cdist(X, kmeans.cluster_centers_, metric=‘euclidean‘), axis=1)) / X.shape[0]) plt.plot(K, mean_distortions, ‘bx-‘) plt.xlabel(‘k‘) font = FontProperties(fname=r‘c:\windows\fonts\msyh.ttc‘, size=20) plt.ylabel(u‘平均畸变程度‘, fontproperties=font) plt.title(u‘用肘部法确定最佳的K值‘, fontproperties=font) plt.show()
输出手肘图
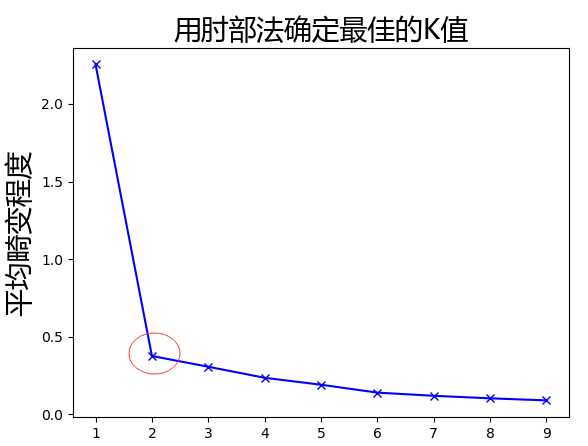
可以明显看出红色圆圈是个肘点。
缺点
1. 不是所有的数据都能呈现这样明显的肘点;
2. 单纯地以数据选择k值,可能脱离实际;
补充
在实际任务中,我们可能根据业务来确定 k 值,如区分男女,k=2,区分人种,k=3,黄黑白;
结合类内聚合度和类间分离度来评价聚类效果。
计算方法
1. 计算样本 i 到同簇内其他样本的平均距离 ai;【ai越小,说明该样本越应该被分到该簇,故可将 ai 视为簇内不相似度】
2. 计算簇内所有样本的 ai;
3. 计算样本 i 到其他簇内所有样本的平均距离 bi,并取min;【bi 视为 i 的类间不相似度,bi为i到其他类的所有bi中min,bi越大,越不属于其他类】
4. 样本 i 的簇内不相似度 ai 和类间不相似度 bi,计算轮廓系数
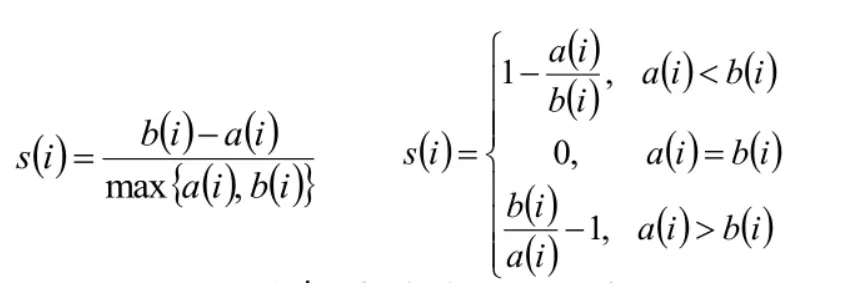
□ s_i 越接近1, 则说明样本 i 聚类合理。
□ s_i 越接近-1,说明样本 i 更适合聚到其他类
□ s_i 越接近0,则说明样本 i 在两个簇的边界上
这种方法计算量大,视情况使用。
参考资料:
https://blog.csdn.net/xiligey1/article/details/82457271
https://www.jianshu.com/p/f2b3a66188f1
标签:资料 detail nbsp 输出 font 情况 大于 info 提升
原文地址:https://www.cnblogs.com/yanshw/p/10955809.html