标签:har dfs include ack its href inline png ora

就是大概这么个东西
根据题意,我们可以清楚的知道:这个题我不会,这个题需要先将2n个数进行排序
这样每对于一个小的前(后)缀和总会在队列最前或队列最后
设这个数为k
那么判断总的Sum(n)-k是否在集合之中就可以啦
当然,如果不在集合之中,我们就要重新的回溯一遍
直到成功
PS:若k既满足于前缀和又满足于后缀和,先放在前面
因为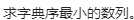
下放代码:
//weight #include <bits/stdc++.h> using namespace std; const int N = 0x3f3f3f3f; int n, s[N], m, a[N], t[N], flag, ans[N], all; inline int read() { int x = 0, y = 1; char z = getchar(); while (z < ‘0‘ || z > ‘9‘) { if (z == ‘-‘) { y = -1; z = getchar(); } } while (z >= ‘0‘ && x <= ‘9‘) { x = (x << 3) + (x << 1) + z - ‘0‘; z = getchar(); } } inline void dfs(int l, int r, int now, int sum1, int sum2) { if (flag) return; if (l == r) { int w3 = all - sum1 - sum2; if (t[w3]) { ans[l] = w3; flag = 1; } return; } int w1 = s[now] - sum1; if (w1 <= 500 && w1 >= 1 && t[w1]) //属于前缀 { ans[l] = w1; dfs(l + 1, r, now + 1, s[now], sum2); } if (flag) return; int w2 = s[now] - sum2; if (w2 <= 500 && w2 >= 1 && t[w2]) //属于后缀 { ans[r] = w2; dfs(l, r - 1, now + 1, sum1, s[now]); } } int main() { scanf("%d", &n); for (int i = 1; i <= 2 * n; i++) //前后缀和 scanf("%d", &s[i]); scanf("%d", &m); for (int i = 1; i <= m; i++) { scanf("%d", &a[i]); t[a[i]] = 1; } sort(s + 1, s + 2 * n + 1); all = s[2 * n]; dfs(1, n, 1, 0, 0); for (int i = 1; i <= n; i++) printf("%d ", ans[i]); return 0; }
标签:har dfs include ack its href inline png ora
原文地址:https://www.cnblogs.com/gongcheng456/p/11007401.html