标签:定义 ref semi uri wol ilo 题解 图像 而且
判断函数 \(f(x)=ln(x+\sqrt{1+x^{2}})\) 的奇偶性。
\(log_{a}(MN)=log_{a}M+log_{a}N\)
在 MATLAB (下面的代码在 MATLAB 9.1.0.441655 (R2016b) 中测试通过) 中输入如下代码:
x=0:0.01:10;
semilogy(x,log(x))可以绘制出 \(y=ln(x)\) 的图像:
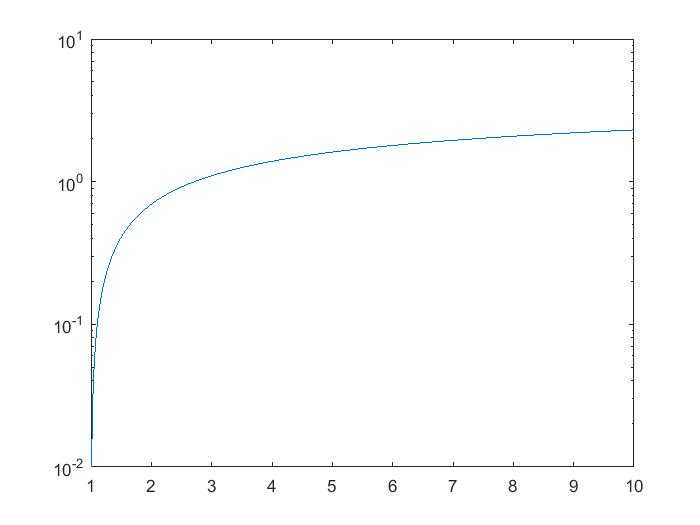
图 1
有图像可以看到,自然对数 \(ln(x)\) 只在 \((0,+\infty)\) 的区间里有定义,不符合对数函数或者偶数函数对于“定义域 \(X\) 关于原点对称”的要求。不过题目中的函数可以看作是一个符合函数,因此,我们还需要结合 \(g(x)=x+\sqrt{1+x^{2}}\) 的定义域来确定 \(f(x)\) 的定义域。
因为:
\(\sqrt{1+x^{2}}>\sqrt{x^{2}}>|x|>0\)
则:
当 \(x\in (-\infty,+\infty)\) 时 \(x+\sqrt{1+x^{2}} > 0\) 满足自然对数函数 \(ln(x)\) 对定义域的要求,而且,当 \(x=0\) 时,\(f(x)=ln(1)=0\), 也满足奇函数“当f(x)在原点处有定义时,f(0)=0”的要求。
到这里,定义域的问题解决了,下面要解决的是函数是关于 \(y\) 轴对称,还是关于原点对称的问题。
由于:
\(f(x)=ln(x+\sqrt{1+x^{2}})\)
\(f(-x)=ln(-x+\sqrt{1+x^{2}})\)
则:
\(f(x)+f(-x)=ln(\sqrt{1+x^{2}}+x)+ln(\sqrt{1+x^{2}}-x)=ln[(\sqrt{1+x^{2}}+x)(\sqrt{1+x^{2}}-x)]=ln(1+x^{2}-x^{2})=ln(1)=0\)
上面的运算结果符合奇函数的定义,因此,\(f(x)=ln(x+\sqrt{1+x^{2}})\) 是一个奇函数。
此外,使用 WolframAlpha 画出的函数 \(f(x)=ln(x+\sqrt{1+x^{2}})\) 的图像如下:

图 2. 图片来自 https://www.wolframalpha.com/
由图像我们也可以看出这是一个奇函数。
EOF
标签:定义 ref semi uri wol ilo 题解 图像 而且
原文地址:https://www.cnblogs.com/zhaokaifeng/p/11015909.html