标签:ring 素数 原来 计算机 构造 叠加 middle 也有 方便
1.顺序查找
顺序查找进行遍历元素,进行查找
总计全部比较次数为:1+2+…+n = (1+n)n/2
若求某一个元素的平均查找次数,还应当除以n(等概率), 即: ASL=(1+n)/2 ,时间效率为 O(n)
解释:ASL表示average search length 平均查找长度
public static void main(String[] args) { int[] a=new int[] {5,1,6,9,2,4,8}; System.out.println(linearSearch(a, 9)); } public static int linearSearch(int[] arr,int searchNum) { int res=-1; for(int i=0;i<arr.length;i++) { if(arr[i]==searchNum) { res=i; break; } } return res; }
2.二分查找法
前提,序列有序
平均每个数据的查找时间还要除以n,所以:
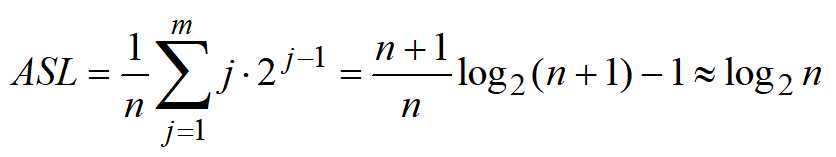
public static void main(String[] args) { int[] a=new int[] {1,2,3,4,5,6,7}; System.out.println(linearSearch(a, 3)); } public static int binarySearch(int[] arr,int searchNum) { int low,high,middle; low=0; high=arr.length-1; middle=(low+high)/2; for(int i=0;i<arr.length;i++) { if(searchNum==arr[middle]) { return middle; }else if(searchNum>arr[middle]) { low=middle; middle=(low+high)/2; }else { high=middle; middle=(low+high)/2; } } return -1; }
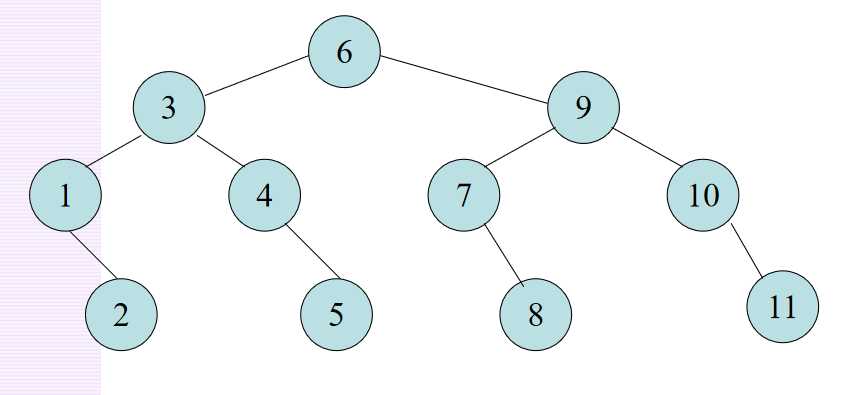
查找过程可用二叉树描述:每个记录用一个结点表示;结点中值为该记录在表中位置,这个描述查找过程的二叉树称为判定树。
n个元素的表的二分查找的判定树是唯一的,即:判定树由表中元素个数决定。
3.分块查找
这是一种顺序查找的另一种改进方法。 先让数据分块有序,即分成若干子表,要求每个子表中的数值(用关键字更准确)都比后一块中数值小(但子表内部未必有序)。
然后将各子表中的最大关键字构成一个索引表,表中还要包含每个子表的起始地址。
① 对索引表使用二分查找法(因为索引表是有序表);
② 确定了待查关键字所在的子表后,在子表内采用顺序查找法(因为各子表内部是无序表);
查找效率分析:ASL=Lb+Lw
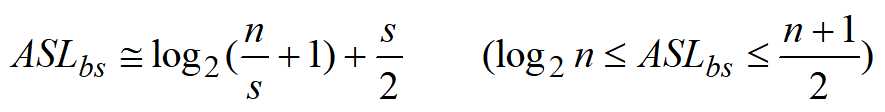
前提:自定义每个区块的数量会影响查找的速度,分块查找在大数据中也有一定的作用,类似大数据的分机器先排序内,再排序外的排序法,只不过这边的区块内部是有序的
4.散列查找(哈希查找)
哈希(Hash)表:即散列存储结构。 散列法存储的基本思想:建立关键码值与其存储位置的对应关系,或者说,由关键码的值决定数据的存储地址。
优点:查找速度极快(O(1)),查找效率与元素个数n无关!
按照计算哈希直接存入计算机地址,Java可以用一个数组空间进行模拟,只要进行计算即可
直接定址法
Hash(key) = a·key + b (a、b为常数) 优点:以关键码key的某个线性函数值为哈希地址,不会产生冲突. 缺点:要占用连续地址空间,空间效率低。
除留余数法
Hash(key)=key mod p (p是一个整数) 特点:以关键码除以p的余数作为哈希地址。
关键:如何选取合适的p? 技巧:若设计的哈希表长为m,P通常取小于或等于散列表长m的最大素数(p≤m),Java中选用了31,因为31正好是2<<5-1
平方取中法
特点:对关键码平方后,按哈希表大小,取中间的若干位作为哈希地址。
理由:因为中间几位与数据的每一位都相关。 例:2589的平方值为6702921,可以取中间的029为地址。
折叠法
特点:将关键码自左到右分成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和(舍去进位)作为散列地址。
法1:移位法 ── 将各部分的最后一位对齐相加。
法2:间界叠加法──从一端向另一端沿分割界来回折叠后,最后一位对齐相加。
例:元素42751896, 用法1: 427+518+96=1041 用法2: 427 518 96—> 724+518+69 =1311
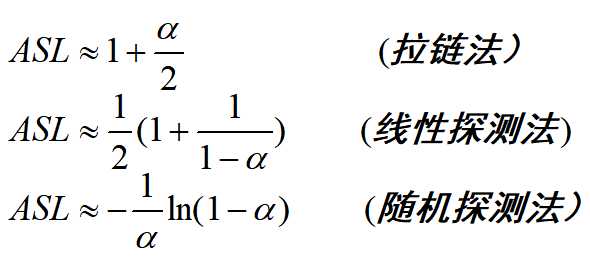
5.二叉排序树(中序序列顺序的树)
关于查找:与根节点比较,如果大则右查找,如果小为左查找
关于插入:按照查找进行插入
关于删除,如果是叶子节点直接删除,如果有一个子树,那么删除后把子节点回归,如果有左右两个子树,那么把左子树的最大或者右子树的最小放在原来节点
6.平衡二叉树(AVL树)(可参考这个博客:https://blog.csdn.net/saasanken/article/details/80796178,关于AVL树)
平衡二叉树又称AVL树,它是具有如下性质的 二叉树:
左、右子树是平衡二叉树; 所有结点的左、右子树深度之差的绝对值≤ 1
即|左子树深度-右子树深度|≤ 1
为了方便起见,给每个结点附加一个数字,给 出该结点左子树与右子树的高度差。这个数字 称为结点的平衡因子balance。这样,可以得到 AVL树的其它性质:
如果在一棵AVL树中插入一个新结点,就有可能造成失衡,此时必须重新调整树的结构,使之恢复平衡。我们称调整平衡过程为平衡旋转。
平衡旋转可以归纳为四类:
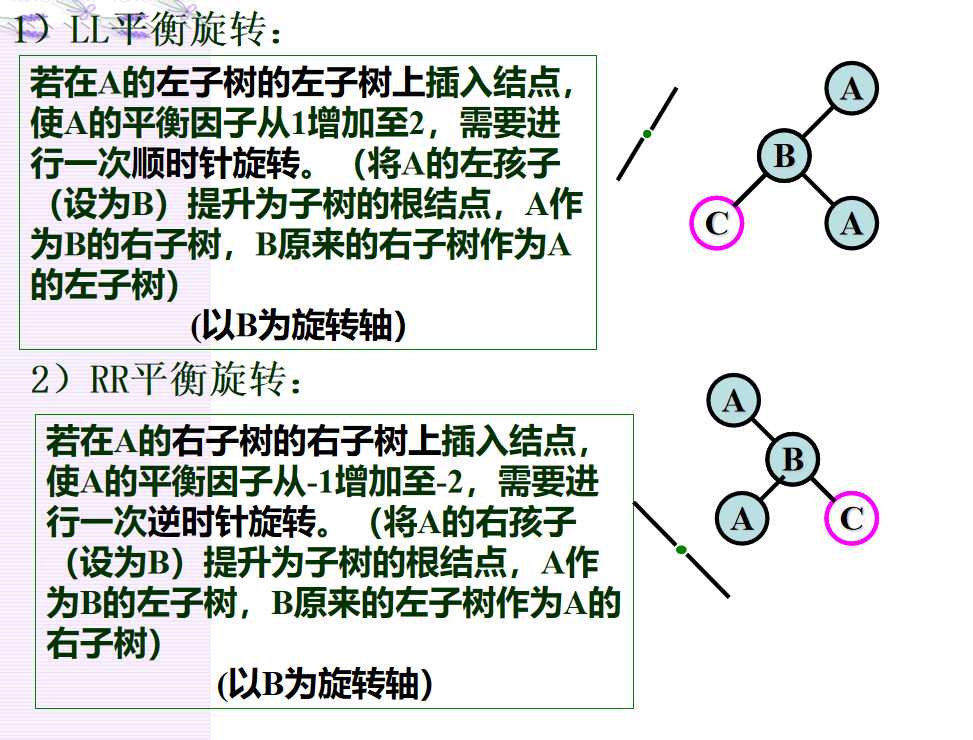
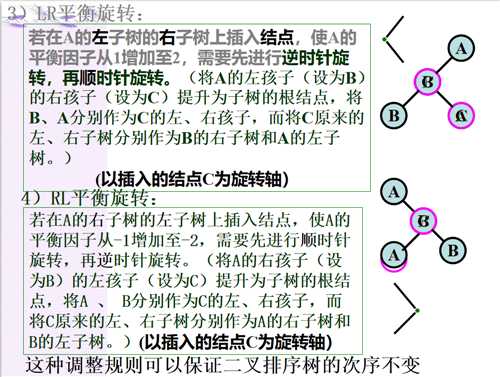
优点和缺点:
优点:层数较少,可以尽快查到
缺点:插入时需要旋转多次,这样会小号大量的磁盘IO
标签:ring 素数 原来 计算机 构造 叠加 middle 也有 方便
原文地址:https://www.cnblogs.com/littlepage/p/11016551.html