标签：个数   rac   title   规范   序列   canonical   anon   mic   数据集   

一、简介

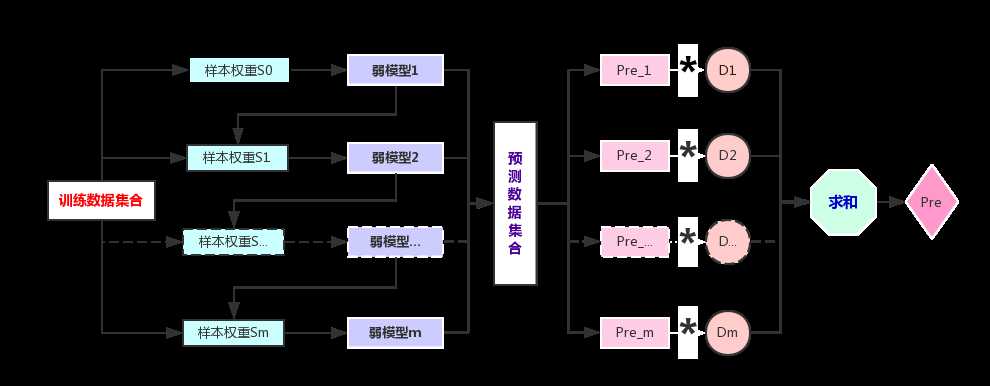
这个方法主要涉及到2个权重集合：

样本的权重集合
每个样本都对应一个权重。 在构建第一个弱模型之前，所有的训练样本的权重是一样的。第一个模型完成后，要加大那些被这个模型错误分类(分类问题)、或者说预测真实差值较大(回归问题)的样本的权重。依次迭代，最终构建多个弱模型。每个弱模型所对应的训练数据集样本是一样的，只是数据集中的样本权重是不一样的。
弱模型的权重集合
得到的每个弱模型都对应一个权重。精度越高(分类问题的错分率越低，回归问题的错误率越低)的模型，其权重也就越大，在最终集成结果时，其话语权也就越大。

二、步骤

1.分类问题

• 训练数据集

　　　令Yi = 1 or -1，这种定义便于后面的结果集成。集合Y0表示数据集样本的真实类别序列。

• 初始的样本权重集合S1，弱模型的权重集合为D　　

　　  n为数据集样本个数，m为要建立的弱模型的个数

• 针对数据集构建弱模型M1，得到这个弱模型的错分率为

　　　假设弱模型M1的训练数据集的预测类别序列为P1，预测数据集的预测类别序列为Pre_1。

          ，

　　   其中Cerror表示被弱模型M1错分的样本个数，CData为全部的样本个数，也就是n。

• 计算弱模型M1的权重

• 更改样本的权重

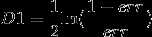
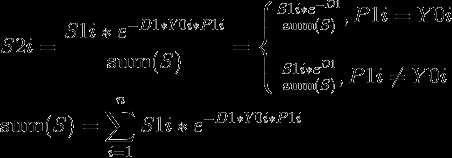
　　  D1为非负数，因此预测正确的样本的权重会比上一次的降低，预测错误的会比上一次的增高。

　　  其中除以sum(S)，相当于将样本权重规范化。

• 迭代

　　  当达到设定的迭代次数时停止，或者错分率小于某个小的正数时停止迭代。

　　  此时得到m个弱模型，以及预测数据集对应的预测结果序列Pre_1，Pre_2， ……Pre_m，

　　  以及模型的权重集合D。

• 结果集成

　　 针对第i个预测样本的集成结果为JI_i,

        ，sign为符号函数。

　　回归问题和分类问题的最大不同在于，回归问题错误率的计算不同于分类问题的错分率，下面给出回归问题的步骤，因为回归算法有很多的变种，这里以Adaboost R2算法为例说明：

2.回归问题

•  训练数据集

          ，输出值的序列为Y0。

• 初始的样本权重集合S1，弱模型的权重集合为D

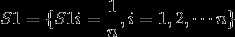
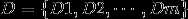
　　  n为数据集样本个数，m为要建立的弱模型的个数

• 针对数据集构建弱模型M1，得到这个弱模型的错误率为

  假设弱模型M1的训练数据集的预测类别序列为P1，预测数据集的预测类别序列为Pre_1。

  

  • 误差损失为线性

    

  • 误差损失为平方

    

  • 误差损失为指数

    

  错误率的计算公式为：

  

adaboost草稿

标签：个数   rac   title   规范   序列   canonical   anon   mic   数据集   

原文地址：https://www.cnblogs.com/nxf-rabbit75/p/11024554.html