标签:dir schedule ges moved nes rnn boolean 编号 state
Amazon‘s distribution network consists of fulfillment centers located in N cities. Some of the cities are directly connected to each other by bidirectional roads. To prepare for the holiday season and satisfy customer demands, items will have to be moved between cities on regularly-scheduled delivery routes. A delivery route is the path that connects the two cities either directly or via some other cities. Amazon-already has delivery routes between some of the cities, but needs to augment this set of routes with additional ones to connect them all. Before any new routes can be developed, new roads need to be constructed such that all cities are accessible from each other. Amazon will be assisting in the planning and construction of the new roads. Write an algorithm to calculate the minimum cost to add new roads between the cities such that all the cities are accessible from each other.
Input
The input to the function/method consists of five arguments:
nurnTotalAvailableCities, an integer representing the total number of cities (N) (e.g., if N = 3, the cities are represented as 1, 2, 3);
numTotalAvailableRoads, an integer representing the total number of currently available roads;
roadsAvailable, a list where each element consists of an integer pair representing the cities directly connected by a road,
numNewRoadsConstruct, an integer representing the total number of roads that can be added;
costNewRoadsConstruct, a list where each element consists of an integer triplet representing the pair of cities between which the road can be added and the cost of addition of the road, respectively (es [1, 3, 10] means to construct a road between cities 1 and 3, the cost would be 10)
Output
Return an integer representing the minimum cost incurred to add new roads such that all the cities are accessible from each other. If there is no solution, return -1
ConItrains
0 <= nurnTotatAvaliableCities <= 50 (ie., total available cities is between 0 and 50)
1 <= costatewRoadsConstruct[i][2]<= 1000 (i.e. the cost to construct any new road is between 1 and 1000)
0 <= i < nurnNewRoadsConstruct
Example
Input:
numTotalAvailableCities = 6
numTotalAvailableRoads = 3
roadsAvallable = [[1,4], [4,5], [2,3]]
numNewRoadsConstruct = 4
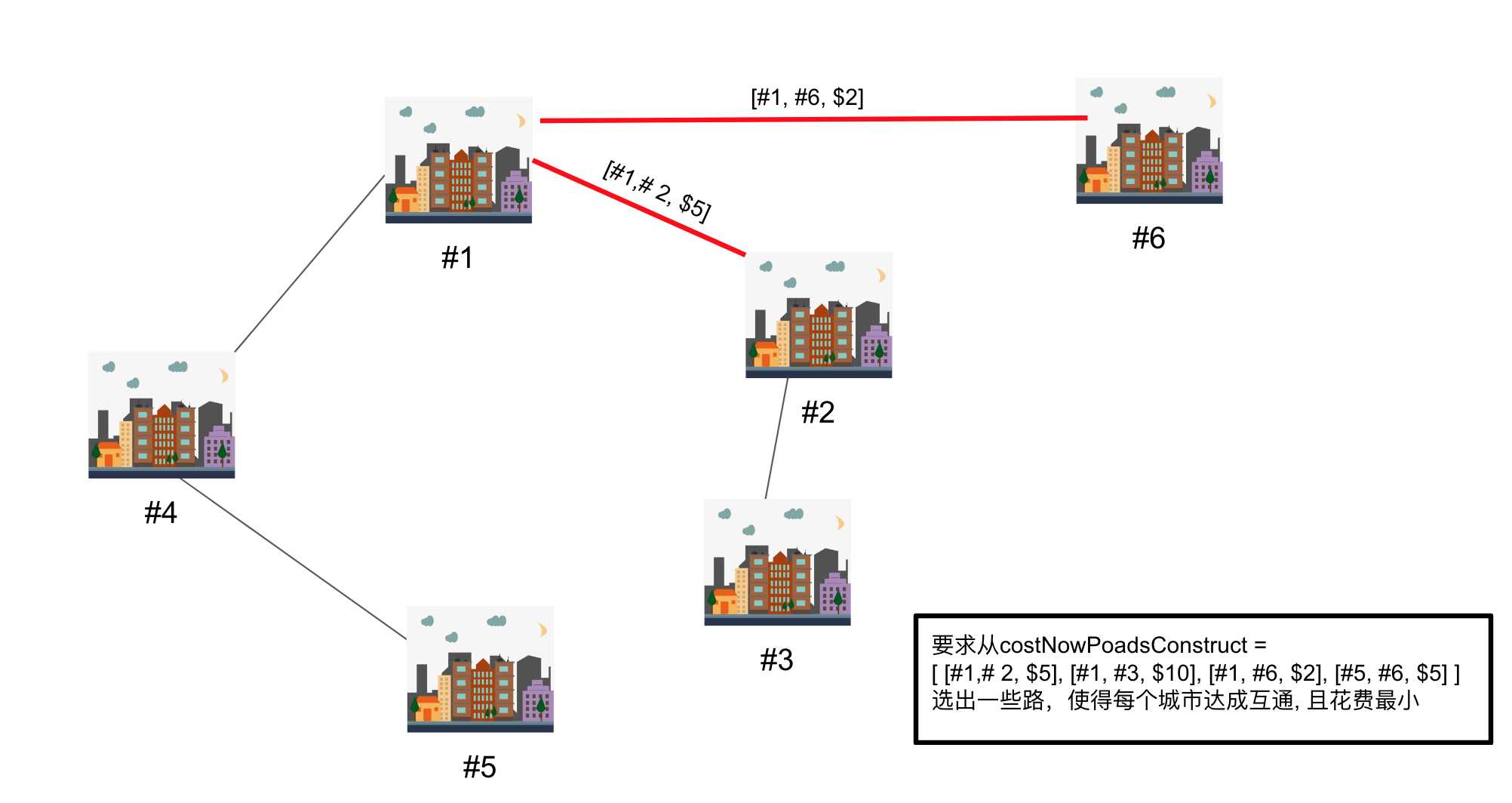
costNowPoadsConstruct = [ [1, 2, 5], [1, 3, 10], [1, 6, 2], [5, 6, 5] ]
Output
7
Explaination:
There are three networks: [1,4,5], [2,3] and [6].
We can connect these networks into a single network by connecting the city 1 to city 2 and city 1 to city 6 at a minimum cost of 5+2
So, the output is 7
题意:
numTotalAvailableCities = 6 意思是城市的编号从 1 到 6。基于提供的 roadsAvailable list, 这 6 个城市中 已经形成了三个岛, 分别为 [1, 4, 5], [2, 3] 和 [6]。 现在要从 costNewRoadsConstruct list 选出一些路,使得每个城市达成互通, 且花费最小
思路
这是个最小生成树(MST)问题。但要注意整个图中已经有一些边了,不是从0开始的最小生成树。具体来说,可以先Union-Find所有已经有的路 in roadsAvailable list,然后把所有可以建的路 in costNewRoadsConstruct list 按照 cost 排序放入 min-heap。然后每次从 min-heap 中拿出最小 cost 的路来接着 Union-Find整个图。每次需要Union的时候,累积目前为止的 cost。当总的 edges 数目等于总的 vertices 数目减 1 时,整个图就被构建成了一颗树。这时输入累积的cost作为输出。
注意:
这个题不太容易过所有的 test case (目前有19个test cases),因为有些坑需要避免。
1. 城市的ID是从1开始,不是从0开始。所以UnionFind的时候要多注意。
2. 输入的roadsAvailable list 和 costNewRoadsConstruct list 互相之间可能有重复。所以不要在算Graph中的 edges 数目的时候要格外注意。
代码
1 import java.util.ArrayList; 2 import java.util.List; 3 import java.util.PriorityQueue; 4 5 public class MinCostToConstruct { 6 int getMinimumCostConstruct(int numTotalAvailableCities, 7 int numTotalAvaiableRoads, 8 List<List<Integer>> roadsAvaiable, 9 int numNewRoadsContruct, 10 List<List<Integer>> costNewRoadsConstruct){ 11 // CORNER CASE 12 if(numTotalAvailableCities < 2 || numTotalAvaiableRoads >= numTotalAvailableCities -1) return 0; 13 14 UnionFind uf = new UnionFind(numTotalAvailableCities); 15 int existingRoadCount = 0; 16 for(List<Integer> pair : roadsAvaiable){ 17 int city1 = pair.get(0); 18 int city2 = pair.get(1); 19 if(!uf.find(city1, city2)){ 20 uf.union(city1, city2); 21 existingRoadCount ++; 22 } 23 } 24 // 网上写法: 25 // PriorityQueue<Connection> pq = new PriorityQueue<Connection>(numNewRoadsContruct, (a,b)->(Integer.compare(a.cost, b.cost)) 26 PriorityQueue<Connection> pq = new PriorityQueue<Connection>((o1, o2) ->o1.cost - o2.cost); 27 for(List<Integer> newRoad: costNewRoadsConstruct){ 28 Connection cn = new Connection(newRoad.get(0), newRoad.get(1), newRoad.get(2)); 29 pq.offer(cn); 30 } 31 32 List<Connection> mst = new ArrayList<>(); 33 34 while(pq.size() > 0 && mst.size() + existingRoadCount < numTotalAvailableCities - 1){ 35 Connection tmpCn = pq.poll(); 36 int city1 = tmpCn.city1; 37 int city2 = tmpCn.city2; 38 if(!uf.find(city1, city2)){ 39 uf.union(city1, city2); 40 mst.add(tmpCn); 41 } 42 } 43 if(mst.size() + existingRoadCount < numTotalAvailableCities -1) return -1; 44 int sum = 0; 45 for(Connection cn : mst){ 46 sum += cn.cost; 47 48 } 49 return sum; 50 } 51 52 class Connection{ 53 int city1; 54 int city2; 55 int cost; 56 public Connection(int city1, int city2, int cost){ 57 this.city1 = city1; 58 this.city2 = city2; 59 this.cost = cost; 60 } 61 } 62 63 class UnionFind{ 64 private int[]ids; 65 public UnionFind(int size){ 66 this.ids = new int[size + 1]; 67 for(int i = 0; i < size + 1; i ++){ 68 this.ids[i] = i; 69 } 70 } 71 72 public int root(int i){ 73 while(ids[i] != i ){ 74 i = ids[i]; 75 } 76 return i; 77 } 78 public boolean find(int i, int j ){ 79 return root(i) == root(j); 80 } 81 public void union(int i , int j ){ 82 int rooti = root(i); 83 int rootj = root(j); 84 ids[rooti] = rootj; 85 } 86 } 87 }
标签:dir schedule ges moved nes rnn boolean 编号 state
原文地址:https://www.cnblogs.com/liuliu5151/p/11026107.html