运筹学-敏感性分析,建立模型

标签：作业   图片   一个   初始   alt   范围   思想   最小   ima   

灵敏度分析

在条件AX = b中若某些b发生了改变时，计算最优解是否改变的方法

对于一个已求解完成的单纯形，我们有

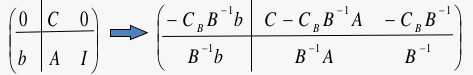
原来是单位阵的地方，现在变成B^-1

解为B^-1*b

当b变为b+ Δb时，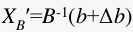

Δb的计算:

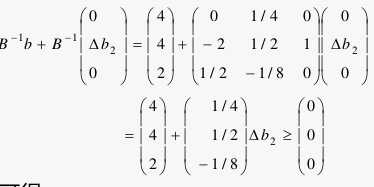
有X必须要>0可以求出b的取值范围

对于Δc的计算

要使得最优解不变则需

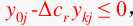
比如C2

那么第一列的2就变成2 + Δc₂ 

那么这个-1.5(第一行) - 0.5(-1.5对应的那一列的对于x2的那一行)*Δc₂ <= 0 

-0.125 - (-0.125) * Δc₂ <= 0 

建立目标规划模型

这个比较简单，就不写了

运输问题的求解与线性规划的关系

表上作业法

利用贪心的思想，先配送运费最小的地方从而得到一个可行解、不断划去以满足的行或列

利用最小元素法给出的初始解是单纯形法求解运输问题的基可行解

运筹学-敏感性分析,建立模型

标签：作业   图片   一个   初始   alt   范围   思想   最小   ima   

原文地址：https://www.cnblogs.com/shensobaolibin/p/11030568.html