2014鞍山现场赛部分题解。

标签：algorithm   dp   iostream   namespace   鞍山邀请赛   

首先说1004，是个比较坑的题目。

题意：给出n个星星的位置，所有质量都为1，在一维坐标上，然后可以移动其中的k个，w是质量，di 是距离质心的距离，要求这样一个值 I 最小。

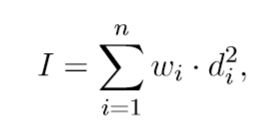
首先说一下质心的定义：质量与位置的成绩和除以质量和。

那么我们可以这样想，移动k个，那么会剩余ff = n - k 个，那么必然留下来相邻的是最优的，我们可以用O（n）的复杂度枚举所有相邻的 ff 个区间，然后求一个最小值。

我们知道 i 求的话，需要知道 di ^2 ,假设质心为 x ，坐标为 xi ，要求（x - xi）^2 = x^2 + xi^2 - 2 *x * xi，我们可以先预处理一个前缀和和前缀平方和，就可以了、

这题很多人没过的坑点在于，他有可能不移动是更优的，所有还要考虑不移动的情况，去一个最小值

AC代码：

#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
#define Del(a,b) memset(a,b,sizeof(a))
const int N = 70000;
double a[N],sum[N];
double seq[N];
int main()
{
    //freopen("Input.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n,k;
        scanf("%d%d",&n,&k);
        int ff = n-k;
        for(int i=1;i<=n;i++)
            scanf("%lf",&a[i]);
        if(ff== 0 || ff==1)
        {
            puts("0");
            continue;
        }
        sort(a+1,a+n+1);
        sum[0] = 0;
        seq[0] = 0;
        for(int i=1;i<=n;i++)
        {
            sum[i]=sum[i-1]+a[i];
            seq[i] = seq[i-1] + (a[i]*a[i]);
        }
//        for(int i=0;i<n;i++)
//            printf("%.2lf ",sum[i]);
        double tmp = sum[n] / ff;
        double ans = seq[n] + ff *tmp *tmp - 2*tmp*sum[n];
        for(int  i = ff;i<=n;i++)
        {
            //printf("YES%d\n",ff);
            tmp = (sum[i] - sum[i-ff])/ff;
            double pps = 0;
            pps = (seq[i] - seq[i-ff]) + ff*(tmp*tmp) - 2 * tmp *(sum[i]-sum[i-ff]);
//            for(int j = i-ff+1;j<=i;j++)
//                pps+=((a[i]-tmp)*(a[i]-tmp));
            //printf("tmp:%.5lf \n",pps);
            ans = min(pps,ans);
        }
        printf("%.10lf\n",ans);
    }
    return 0;
}

直接枚举所有情况dp【i】【j】合并前 i 个第 i 个是第 j 个的结果

转移方程：

 dp[i][k] = max(dp[i][k],dp[i-1][j]+a[j][k]);

直接上代码：

#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
#define Del(a,b) memset(a,b,sizeof(a))
const int N = 120;
int dp[N][60];
int a[60][60];
int s[N];
int main()
{
    //freopen("Input.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=m;i++)
            for(int j = 1;j<=m;j++)
                scanf("%d",&a[i][j]);
        memset(dp,-1,sizeof(dp));
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&s[i]);
        }
        if(s[1]!=-1)
            dp[1][s[1]] = 0;
        else
            for(int i=1;i<=m;i++)
                dp[1][i] = 0;
        for(int i=2;i<=n;i++)
        {
            for(int j = 1;j<=m;j++)
            {
                if(dp[i-1][j] == -1)
                    continue;
                if(s[i]!=-1)
                {
                    //printf("NO\n");
                    dp[i][s[i]] = max(dp[i][s[i]],dp[i-1][j]+a[j][s[i]]);
                    continue;
                }
                for(int k = 1;k<=m;k++)
                {
                    //printf("YES\n");
                    dp[i][k] = max(dp[i][k],dp[i-1][j]+a[j][k]);
                }
            }
        }
        int ans = 0;
        for(int i=1;i<=m;i++){
            //printf("%d %d\n",i,dp[n][i]);
            ans = max(ans,dp[n][i]);
        }
        printf("%d\n",ans);
    }
    return 0;
}

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;

const int N = 1005;
struct POINT
{
    double x, y;
    double t;
}p[N];

double dis(POINT a, POINT b)
{
    return sqrt(pow(a.x - b.x, 2.0) + pow(a.y - b.y, 2.0));
}

int main()
{
    int T;
    scanf("%d", &T);
    while(T --){
        int n;
        scanf("%d", &n);
        for(int i = 0; i < n; i ++){
            scanf("%lf %lf %lf", &p[i].t, &p[i].x, &p[i].y);
        }
        double ans = 0.0;
        for(int i = 1; i < n; i ++){
            ans = max(ans, dis(p[i], p[i - 1]) / (p[i].t - p[i -1].t));
        }
        printf("%.10lf\n", ans);
    }
    return 0;
}

2014鞍山现场赛部分题解。

标签：algorithm   dp   iostream   namespace   鞍山邀请赛   

原文地址：http://blog.csdn.net/y990041769/article/details/40378447