标签:顺序 == 相加 不用 中间 图片 程序员 转换 组成
在编程工作种,我们时常需要对不同的进制的数进行转换,以方便我们的工作、阅读和理解。在计算机领域,主要设计二进制、八进制、十进制和十六进制,下面我们就来讲讲这四种机制的整数相互转换方法。
一、查表法
就是我们制作一张包含各种进制的值一 一对应数值表,需要时查表就得,但是,我们知道,这不太现实,因为数是无穷的,我们不可能做一张无穷的表。在次但是,这也不是说查表法就不用了,其实我们一直在使用,你可能会说,没有,没见过,不对,有的,就在你的脑海里,我相信绝大部分程序员都有,比如,问你,(15)10对应的十六进制是多少,你肯定张口就答(F)16,为什么你能很快答出,是因为我们在日常工作和学习中,无形在脑海里建立了这张表。只是这张表很有限,更大的数你就不能一口答了,所以需要其他的转换方法。
我们至少要建立起如下的一张表
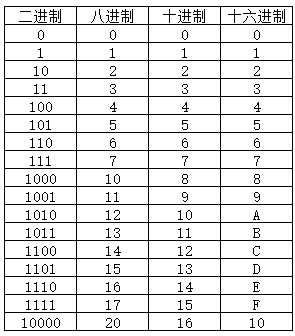
二、短除法
短除法运算方法是先用一个除数除以能被它除尽的一个质数,以此类推,除到商是质数为止。具体在我们的进制换算里,当一个M进制数转N进制数时,就是用这个数除N取余,逆序排列。具体做法是:将N作为除数,用M进制整数除以N,可以得到一个商和余数;保留余数,用商继续除以N,又得到一个新的商和余数;仍然保留余数,用商继续除以N,还会得到一个新的商和余数;如此反复进行,每次都保留余数,用商接着除以N,直到商为0时为止
下面举例:
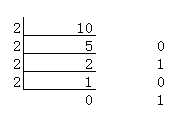
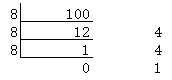
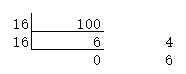

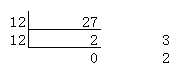

结果,(756)8--->(1EE)16
二进制转其他进制和十六进制转其他进制我就不一一举例了,通过上面的例子,我们可以看到用短除法我们是可以进行任意进制的相互转换的,同时我们也可以发现,将高进制向低进制(只限于这几种进制,我们姑且认为高低顺序为:二进制<八进制<十进制<十六进制)转换时,要先有一步进制基数的查表换算过程,在加上我们人对二、八、十六进制的四则运算不熟悉,所以这三种进制进行短除法换算比较困难。由于十进制的基数本身就是十六进制的数码,同时代表的量意义也一样,所以总的来说,短除法特别适合十进制向二、八、十六进制的转换。三、位权相加法
我们知道,任何进制的数都是由:位、数码、位权等要素构成,这也为我们进制间的转换提供了一种方法:位权相加法。假设当前数字是N进制,那么:对于整数,从右往左看,第i位的位权等于Ni-1。更加通俗的理解是,假设一个多位数(由多个数字组成的数)某位上的数字是1,那么它所表示的数值大小就是该位的位权。当我们由M进制转为N进制时要进行这样的运算:a*Ni-1+aNi-2+...+a*N1+a*N0。
下面举例:
我们可以看到,位权相加法特别适合二、八、十六进制转十进制,对其它情况则很困难,特别是高进制转低进制更是困难。
四、借桥法
对某些困难的情况,我们可以先转位十进制或二进制,然后在转为对应的进制,我成为借桥法,中间的进制就是桥。比如十六进制转八进制,我们可以先用位权相加法转为十进制,在用短除法转为八进制。这就不举例了。
五、总结
标签:顺序 == 相加 不用 中间 图片 程序员 转换 组成
原文地址:https://www.cnblogs.com/yilang/p/11050115.html