标签:code mic 它的 最优 oid memset mamicode ems 蓝色
http://acm.hdu.edu.cn/showproblem.php?pid=2196
题意:给你一棵树,已知每条边的权值。求每个点所能达到的最远点的距离。
思路:先将无根树转为有根树,比如以1为根,对于每个点来说它所能达到的最远距离,就是已自身为根结点向下dfs最大的距离,或者通过自身父节点,在加上父节点不经过自身所能达到的最远距离(这时又有两种情况,1.父节点最远距离是以它为根结点向下产生(如果最远距离经过这个子节点需要考虑父节点向下的第二远的距离),2.父节点也是通过它的父节点产生的最远距离)
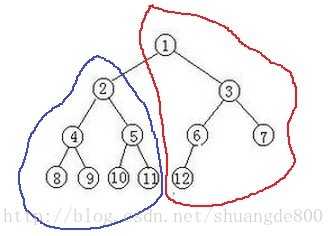
比如下图,对于2点来说,它的最远距离可能是以它为根的子树(蓝色部分)产生的最大值,或者,通过它父节点不经过本身结点所能达到的最远点(也就是整棵树除蓝色部分,相当于红色部分)。
此时
设f(x,0)表示以x为根形成的子树,x所能达到的最远距离
f(x,1)表示,以x为根形成的子树,x所能达到的第二远的距离
f(x,2)表示,x通过父节点不经过自身结点,所能达到的最远距离
对于f(x,0)和f(x,1)可以通过一遍dfs一次得到。
对于f(x,2)可以通过已知父节点的f(x,0)f(x,1)f(x,2)的最优情况,来推出子节点的最优情况,还是从根向子节点遍历一遍求出答案。
每个点答案就是Max(f(x,0),f(x,2))
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e4+10;
#define ll long long
int head[maxn],ver[maxn],nxt[maxn],edge[maxn];
int tot;
ll f[maxn][3];
int rx[maxn];
void dfs1(int x,int fa)
{
for(int i=head[x]; i; i=nxt[i])
{
int y=ver[i];
int w=edge[i];
if(y==fa) continue;
dfs1(y,x);
if(f[x][0]<=f[y][0]+w)
{
f[x][1]=f[x][0];
f[x][0]=f[y][0]+w;
rx[x]=y;
}
else if(f[y][0]+w>f[x][1])
f[x][1]=f[y][0]+w;
else if(f[y][1]+w>f[x][1])
f[x][1]=f[y][1]+w;
}
}
void dfs2(int x,int fa)
{
for(int i=head[x]; i; i=nxt[i])
{
int y=ver[i];
if(y==fa) continue;
int w=edge[i];
if(rx[x]==y)
f[y][2]=max(f[x][1]+w,f[x][2]+w);
else
f[y][2]=max(f[x][0]+w,f[x][2]+w);
dfs2(y,x);
}
}
void add(int u,int v,int w)
{
edge[++tot]=w;
ver[tot]=v;
nxt[tot]=head[u];
head[u]=tot;
}
int main()
{
int n;
while(~scanf("%d",&n))
{
tot=0;
memset(f,0,sizeof(f));
memset(rx,0,sizeof(rx));
memset(head,0,sizeof(head));
for(int i=2; i<=n; i++)
{
int v,w;
scanf("%d%d",&v,&w);
add(i,v,w);
add(v,i,w);
}
dfs1(1,1);
dfs2(1,1);
for(int i=1; i<=n; i++)
{
printf("%lld\n",max(f[i][0],f[i][2]));
}
}
}
标签:code mic 它的 最优 oid memset mamicode ems 蓝色
原文地址:https://www.cnblogs.com/dongdong25800/p/11056413.html