机器学习概述

标签：利用   样本   原理   图片   code   应用   img   输入数据   src   

机器怎么学习？

　　处理某个特定的任务，以大量的“经验”为基础；

　　对任务完成的好坏，给予一定的评判标准；

　　通过分析经验数据，任务完成得更好了；

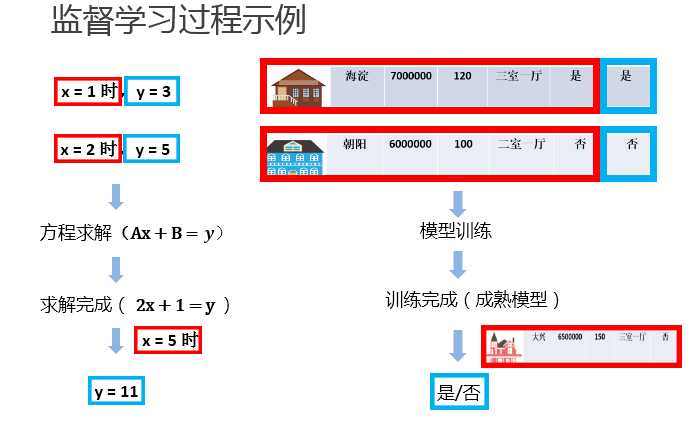
输入海量训练数据对模型进行训练，使模型掌握数据所蕴含的潜在规律，进而对新输入的数据进行准确的分类或预测。

机器学习主要分类：

无监督学习（Unsupervised Learning）：提供输入数据并且不提供数据对应结果的机器学习过程。

　　　　　　寻找数据中的内在共性结构特征来进行样本点的分组或聚类；对于一个新数据，可以通过判断其中是否存在这种特征，来做出相应的反馈；

　　　　　　核心应用是统计学中的密度估计和聚类分析，无监督聚类应用的一个例子就是在谷歌新闻中：分组，组成有关联的新闻，然后按主题显示给用户。

强化学习：通过与环境交互并获取延迟返回进而改进行为的学习过程。

有监督学习：提供输入数据并提供数据对应的输出结果模型的机器学习过程。（主要分为分类和回归）

　　　　　　①当输出被限制为有限的一组值（离散数值）时使用分类算法；

　　　　　　②当输出可以具有范围内的任何数值（连续数值）时使用回归算法。

　　　　　　③相似度学习是和回归和分类都密切相关的一类监督机器学习，它的目标是使用相似性函数从样本中学习，这个函数可以度量两个对象之间的相似度或关联度。它在排名、推荐系统、视觉识别跟踪、人脸识别等方面有很好的应用场景。

　　　　　　应用于预测房价或房屋出售情况。

监督学习三要素：

模型（model）：总结数据的内在规律，用数学函数描述的系统

策略（strategy）：选取最优模型的评价准则

算法（algorithm）：选取最优模型的具体方法

步骤：

①得到一个有限的训练数据集；②确定包含所有学习模型的集合

③确定模型选择的准则，也就是学习策略；  ④实现求解最优模型的算法，也就是学习算法

⑤通过学习算法选择最优模型；⑥利用得到的最优模型，对新数据进行预测或分析

模型评估策略

模型评估
　　训练集和测试集
　　损失函数和经验风险
　　训练误差和测试误差
模型选择
　　过拟合和欠拟合
　　正则化和交叉验证
训练集：输入到模型中对模型进行训练的数据集合。
测试集：模型训练完成后测试训练效果的数据集合。

 损失函数

损失函数用来衡量模型预测误差的大小。
　　定义：选取模型f为决策函数，对于给定的输入参数 X，f(X) 为预测结果，Y为真实结果；
　　f(X)和Y之间可能会有偏差，我们就用一个损失函数（loss function）来度量预测偏差的程度，记作 L(Y,f(X))
　　损失函数是系数的函数
　　损失函数值越小，模型就越好

风险和误差

经验风险
　　模型 f(X) 关于训练数据集的平均损失称为经验风险（empirial risk），记作 R_emp

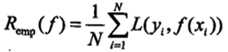
经验风险最小化（Empirical Risk Minimization，ERM）
　　这一策略认为，经验风险最小的模型就是最优的模型
　　样本足够大时，ERM 有很好的学习效果，因为有足够多的“经验”
　　样本较小时，ERM 就会出现一些问题

训练误差
　　训练误差（training error）是关于训练集的平均损失。

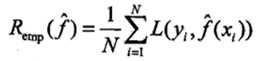
　　训练误差的大小，可以用来判断给定问题是否容易学习，但本质上并不重要；
测试误差
　　测试误差（testing error）是关于测试集的平均损失。

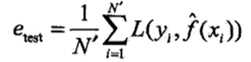
　　测试误差真正反映了模型对未知数据的预测能力，这种能力一般被称为泛化能力；

过拟合和欠拟合

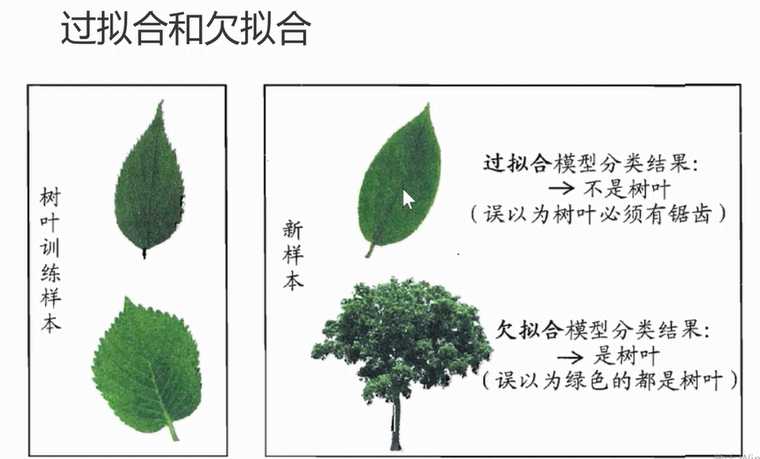
　　模型没有很好地捕捉到数据特征，特征集过小，导致模型不能很好地拟合数据，称之为欠拟合（under-fitting）。
欠拟合的本质是对数据的特征“学习”得不够

　　把训练数据学习的太彻底，以至于把噪声数据的特征也学习到了，特征集过大，这样就会导致在后期测试的时候不能够很好地识别数据，
即不能正确的分类，模型泛化能力太差，称之为过拟合（over-fitting）。 （把局部特质学习成全局）

模型的选择

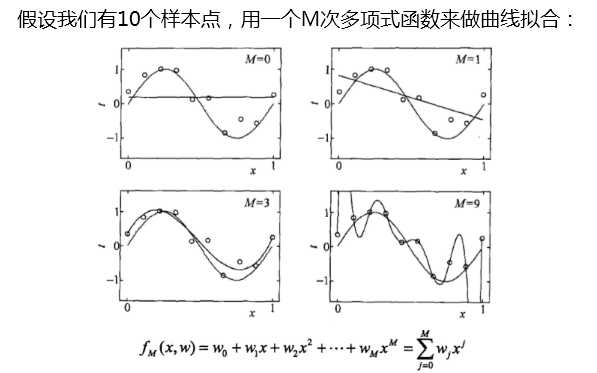
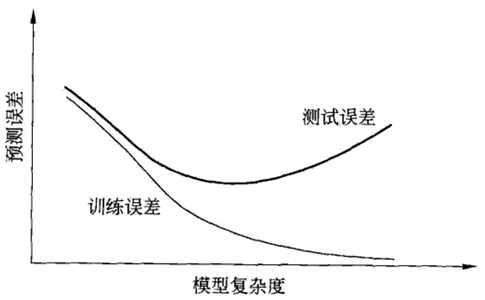
　　当模型复杂度增大时，训练误差会逐渐减小并趋向于0；而测试误差会先减小，达到最小值之后再增大
　　当模型复杂度过大时，就会发生过拟合；所以模型复杂度应适当

正则化：

结构风险最小化（Structural Risk Minimization，SRM）

• 是在 ERM 基础上，为了防止过拟合而提出来的策略
• 在经验风险上加上表示模型复杂度的正则化项（regularizer），或者叫惩罚项
• 正则化项一般是模型复杂度的单调递增函数，即模型越复杂，正则化值越大

结构风险最小化的典型实现是正则化（regularization）
形式：

• 　　第一项是经验风险，第二项 J (f ) 是正则化项， 是调整两者关系的系数
• 　　正则化项可以取不同的形式，比如，特征向量的L1范数或L2范数

奥卡姆剃刀

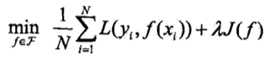
　　奥卡姆剃刀(Occam‘s razor)原理：如无必要，勿增实体
　　正则化符合奥卡姆剃刀原理。它的思想是：在所有可能选择的模型中，我们应该选择能够很好地解释已知数据并且十分简单的模型
　　如果简单的模型已经够用，我们不应该一味地追求更小的训练误差，而把模型变得越来越复杂

交叉验证

数据集划分

• 如果样本数据充足，一种简单方法是随机将数据集切成三部分：训练集（training set）、验证集（validation set）和测试集（test set）
• 训练集用于训练模型，验证集用于模型选择，测试集用于学习方法评估

数据不充足时，可以重复地利用数据——交叉验证（cross validation）
简单交叉验证

• 数据随机分为两部分，如70%作为训练集，剩下30%作为测试集
• 训练集在不同的条件下（比如参数个数）训练模型，得到不同的模型
• 在测试集上评价各个模型的测试误差，选出最优模型

S折交叉验证

• 将数据随机切分为S个互不相交、相同大小的子集；S-1个做训练集，剩下一个做测试集
• 重复进行训练集、测试集的选取，有S种可能的选择

留一交叉验证

分类和回归：

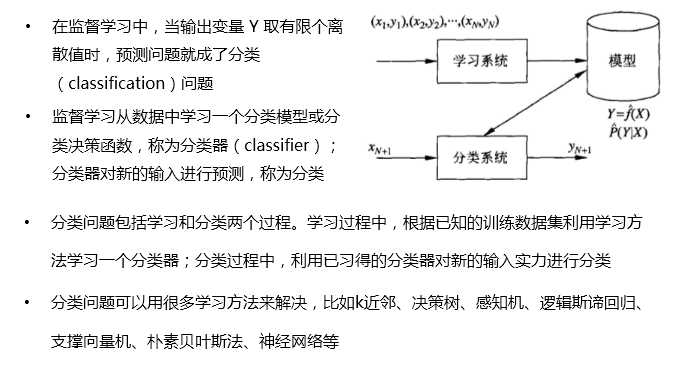
监督学习问题主要可以划分为两类，即 分类问题 和 回归问题

• 分类问题预测数据属于哪一类别。 —— 离散
• 回归问题根据数据预测一个数值。 —— 连续

通俗地讲，分类问题就是预测数据属于哪一种类型，就像上面的房屋出售预测，通过大量数据训练模型，然后去预测某个给定房屋能不能出售出去，属于能够出售类型还是不能出售类型。
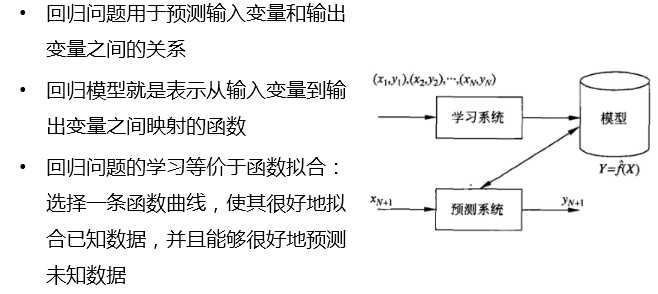
　　回归问题就是预测一个数值，比如给出房屋一些特征，预测房价
如果将上面的房屋出售的问题改为预测房屋出售的概率，得到的结果将不再是可以售出（1）和不能售出（0），将会是一个连续的数值，例如 0.5，这就变成了一个回归问题

 回归问题：

精确率和召回率：

回归问题：

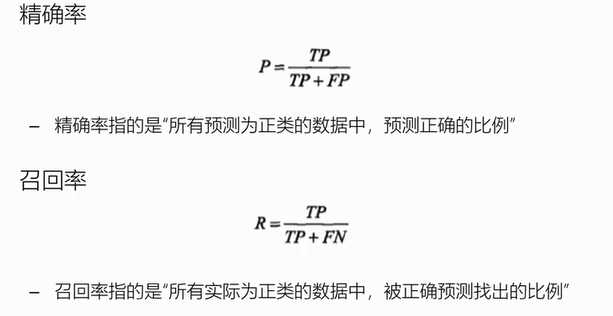
回归问题的分类

• 按照输入变量的个数：一元回归和多元回归
• 按照模型类型：线性回归和非线性回归

回归学习的损失函数 —— 平方损失函数
如果选取平方损失函数作为损失函数，回归问题可以用著名的 最小二乘法（least squares）来求解

 梯度下降算法

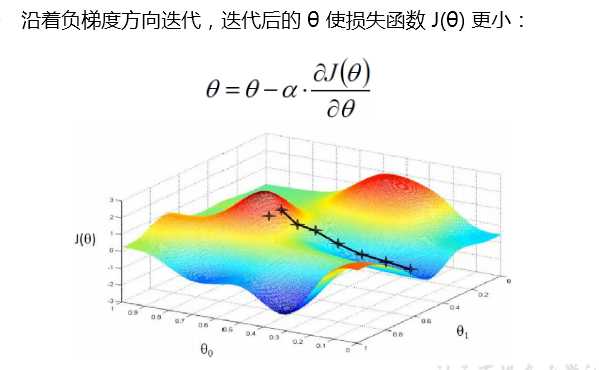
　　梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解
　　如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解

机器学习概述

标签：利用   样本   原理   图片   code   应用   img   输入数据   src   

原文地址：https://www.cnblogs.com/shengyang17/p/11037582.html