标签:style blog http color os ar for sp div
又是计算几何,我感觉最近对计算几何上瘾了。
当然,工作上也会用一些,不过工作上一般直接调用boost的geometry库。
上次写过最小包围圆,这次是最小包围矩形,要比最小包围圆复杂些。
最小包围矩形可不一定是个直立的矩形,也可能像下图一样是倾斜的。
求法如下:
1.求多边形凸包,这里凸包直接调用系统函数了,细节可以参考这里,虽然当时写的不怎么样。
2.将凸包两个相邻的点连线作为矩形一条边。
3.寻找凸包上距离已得到的边最远的点,过该点做平行线,得到矩形第二条边。
4.将凸包上点向已求得的边投影,求得投影点相距最远的两个点,过该两点做直线,作为矩形另外两条边。
5.遍历凸包所有相邻两点从新运行2~4,将面积最小的矩形作为求得结果。
通常情况下,矩形会过随机点中的5个点。
结果如下:
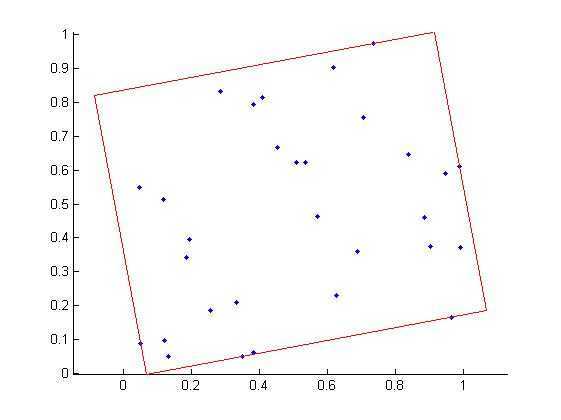
matlab代码如下:
clear all;close all;clc; n=30; p=rand(n,2); ind=convhull(p(:,1),p(:,2)); l=length(ind); hull=p(ind,:); %随机点凸包 area=inf; for i=2:l p1=hull(i-1,:); %凸包上两个点 p2=hull(i,:); k1=(p1(2)-p2(2))/(p1(1)-p2(1)); %连接两点的直线,作为矩形的一条边 b1=p1(2)-k1*p1(1); d=abs(hull(:,1)*k1-hull(:,2)+b1)/sqrt(k1^2+1); %所有凸包上的点到k1,b1直线的距离 [h ind]=max(d); %得到距离最大的点距离,即为高,同时得到该点坐标 b2=hull(ind,2)-k1*hull(ind,1); %相对k1,b1直线相对的另一条平行边k1,b2; k2=-1/k1; %以求得的直线的垂线斜率 b=hull(:,2)-k2*hull(:,1); %过凸包所有点构成的k2,b直线系 x1=-(b1-b)/(k1-k2); %凸包上所有点在已求得的第一条边的投影 y1=-(-b*k1+b1*k2)/(k1-k2); x2=-(b2-b)/(k1-k2); %凸包上所有点在已求得的第二条边的投影 y2=-(-b*k1+b2*k2)/(k1-k2); [junk indmax1]=max(x1); %投影在第一条边上x方向最大与最小值 [junk indmin1]=min(x1); [junk indmax2]=max(x2); %投影在第二条边上x方向最大与最小值 [junk indmin2]=min(x2); w=sqrt((x1(indmax1)-x1(indmin1))^2+(y1(indmax1)-y1(indmin1))^2); %矩形的宽 if area>=h*w %使面积最小 area=h*w; pbar=[x1(indmax1) y1(indmax1); %矩形四个角点 x2(indmax2) y2(indmax2); x2(indmin2) y2(indmin2); x1(indmin1) y1(indmin1)]; end end pbar(5,:)=pbar(1,:); hold on; plot(p(:,1),p(:,2),‘.‘); plot(pbar(:,1),pbar(:,2),‘r‘) axis equal;
标签:style blog http color os ar for sp div
原文地址:http://www.cnblogs.com/tiandsp/p/4044282.html