标签:方式 表示 椭圆 block 也会 问题 html 一个 file
曾经的《几何学观止》我觉得并没有写出我想要的感觉,事实证明原本的想法并不是一个好的主意。
但是,我又有了新的主意,这次我从例子出发,首先从不同角度出发,介绍了代数拓扑,微分流形甚至代数几何,椭圆曲线,表示论视角下的不同几何对象,另外把一些『等同』写出来,我觉得这样才有『叹为观止』的感觉。
当然,这些都只是故事的开始,数学永没有观止的一天。
附1:目录
Preface i
Contents iii
1 二维平面 $\mathbb{R}^2$ 1
2 一维圆周 $\mathbb{S}^1$ 15
3 二维球面 $\mathbb{S}^2$ 28
4 二维轮胎面 $\mathbb{T}^2$ 44
5 射影平面 $\mathbb{P}^2$ 60
6 上半平面 $\mathbb{H}^2$ 76
7 三维正交群 $\mathsf{SO}_3$ 92
List of Figures 108
Index 112
附2:前言
首先, 我认为自己的几何水平并不高, 严格意义上说我只是一个 “几何爱好者”, 本书只是一些我喜欢的, 并且乐于谈论的几何常识. 由于个人的学识有限, 也受制于学习经历, 当中有错误或有偏颇也在所难免, 还请诸位方家斧正.
何谓 “几何”, 这是一个曾经被热烈讨论的议题. 我认为, 简单来说, 就是关于 “形” 的数学. 不论是公理化的几何, 代数拓扑, 微分几何, 代数几何, 能够 “被看见” 往往是第一步. 因此代数拓扑, 微分几何, 代数几何都被我归入广义的 “几何” 门类下.
但是现在很多 “几何” 书, 图的数量实在少的可怜. 我认为一个原因是抽象. 诚然, 现代数学是高度抽象的, 但是往往抽象是建立在具体的, 甚至可以说是 “可见的” 的例子或者现象之上. 因此我挑选了很经典的那些几何对象, 从不同角度提供一些现象, 解释或者计算. 这些例子其实都是几何学家所能熟练把玩的几何对象. 我认为另一原因在于几何的 “感觉”. 很多时候我们需要把“感觉” 传达到位往往词不达意, 因此我尽量多地插图和用 “生动形象” 的语言描述和解释.
在谈论过程中用到了很多拓扑和几何的概念和定理, 我认为这不可避免的, 而且使用起来也无可厚非. 不理解则跳过理解能够理解的, 或者部分理解再以此为动机去学习相关理论都是健康的阅读方式. 另外, 几何无可避免地记号多且不自明, 我会尽量采用最自明的记号和解释说明来描述. 几何学的各个角度看待同一事物会有不同的理解方式, 几何与其他数学分支相互交融, 也会产生不同的观点. 这是我认为几何的妙处之一, 也是我最想在书中体现的.
同时我还好为人师地安排了一些习题. 这些内容往往能再提供一些例子或者理解方式, 或者隐射到更深层面的内容.
每章最后附了一些参考文献, 这并非意味着我认同其写作模式, 或者可以在上面看到我提到的某种理解方式, 只是在这些书上可以找到我提到的结论.实际上, 采用这种不严格的参考文件格式实在是因为, 有不少解释和感觉是我自己想通的, 找不到落实到文字上的文献. 如果你喜欢我的理解方式我感到非常荣幸, 但是专业学习宜咨询专家, 而我只是一个爱好者.
感谢免费好用的作图软件 ipe, 本书中所有插图都是由其制作. 感谢俄罗斯圣彼得堡国立大学对我的赏识, 让我能够静下心来编纂这本书.
最后尤其感谢朱奕这段时间和我讨论很多数学问题, 很多问题是几何的.而且他也教会我一些几何. 为了表示感谢, 他在本书中拥有一整页有着他喜欢动漫角色的专属页面.
熊锐
2019 年 6 月 17 日凌晨
附3:精选画廊
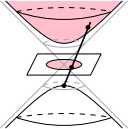
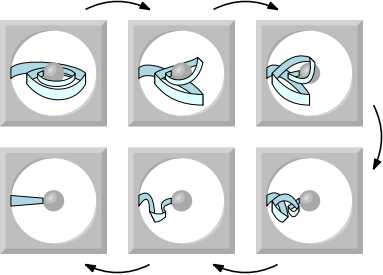
附4:封面

标签:方式 表示 椭圆 block 也会 问题 html 一个 file
原文地址:https://www.cnblogs.com/XiongRuiMath/p/11075081.html