标签:总决赛 学习 是什么 表示 机器 amazon inf strong 阅读
目录
最近在学习统计学相关的知识,在阅读《Head First 统计学》的过程中,遇到了标准差这个概念,当时理解的不是很透彻,就这样略过阅读下面的章节。
直到最近在学习PMP过程中看到了杨述老师对标准差概念的讲解,虽然简单,但是使我对标准差的理解一下子就提升了一大半,因此在这里我试着记录下来,一来巩固理解,二来测试一下自己是否真的理解到位了,毕竟,只有说的明白,才算是真的理解。
篮球教练在招收球员入队的时候,需要有一系列的指标作为入队标准;当两个球员的身体素质等都差不多的时候,就很难抉择该选择谁入队,这时候标准差就是一个非常好的参考;
同样,我们在做两个球星的差距的时候,标准差就能非常有效的描述差距的大小。
西格玛标准差其实是衡量数据或概率分布的曲线的胖瘦。
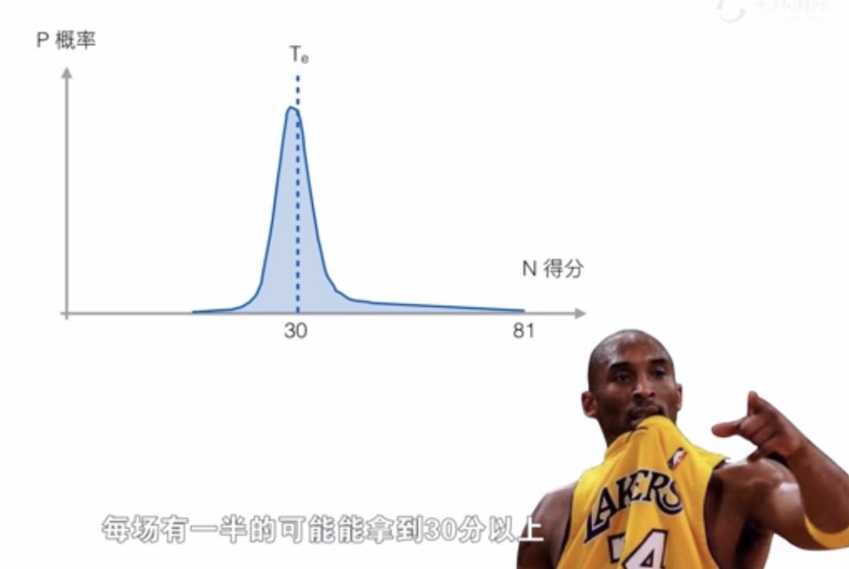
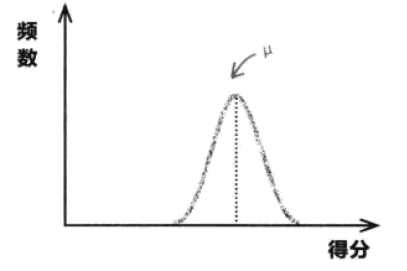
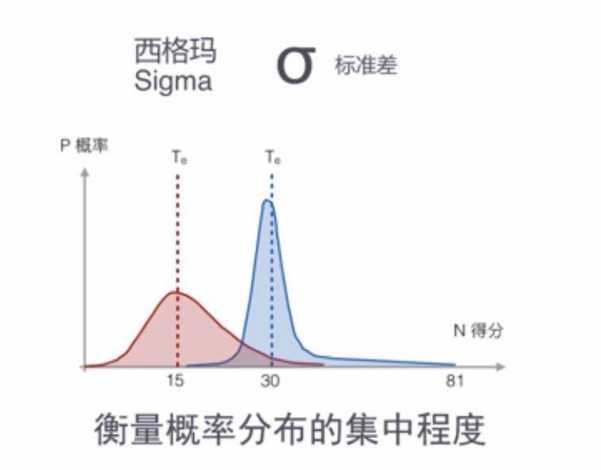
标准差是描述数据或概率分布的集中程度。标准差大小,数据/概率都离这个期望值不远;反之,如果标准差大则表示数据/概率离期望值很远,什么都有可能发生。
举一个极端不稳定的情况,一个球员上场要么得60分,要么得0分,那么均值看起来是30分,和科比一样高呢。但是这样的球员你敢在总决赛那天送他上场吗?你送他上场,他送你上天。
因此均值显然没有体现事情的全部真像,你正在需要知道的是变化幅度(Variance)。均值给出了平均数,而标准差给出了分散程度。
不一定,如果你是找出每场发挥稳定的球员,标准差小就是你要找的人;或者是你正在生存机器零件,标准差小那么零件越一致。
如果你准备入职一家新公司准备大干一场,如果这家公司工资的标准差很小,表示你大干一场或者不干都差不多,你也许应该找一家标准差大的公司大干一场。
标准差的平方就是方差。由于在统计带有负号的数据的时候,如果不用平方最后求出来的标准差可能为0,因此才产生了方差。具体两者关系可以参考《Head First 统计》
就是方差的根号:
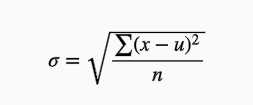
其中:x表示一组数据集内的每一个数据,u表示这组数据集的均值, n表示数据集内的个数。
又可以简化成:
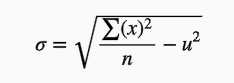
标签:总决赛 学习 是什么 表示 机器 amazon inf strong 阅读
原文地址:https://www.cnblogs.com/wanglee/p/11076254.html