标签:分治 center set cout div 数字 完全 font 位置
残缺棋盘的覆盖问题
问题描述:
在一个有2N ×2N个方格组成的棋盘中,有一个方格残缺(残缺方格位置随机),要求用如下①~④的三格板完全覆盖棋盘中为残缺的方格。

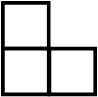
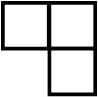
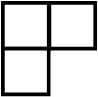
① ② ③ ④
例如:
下面是一个4×4的棋盘,其中黑色的方格代表残缺的方格。

使用三格板覆盖后如下图,其中相同的数字表示同一块三格板。
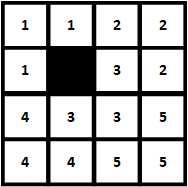
分析:

1×1 2×2 4×4 8×8
当棋盘大小为1×1时,棋盘残缺,不需要三格板覆盖;当棋盘大小为2×2时,有一个方格残缺,用一个三格板正好能完全覆盖;当棋盘越来越大时,覆盖棋盘的方式便较难确定。但是棋盘较小时,问题就比较容易解决了,所以可以采用分治法来解决。

上图是一个4×4的残缺棋盘,我们可以将这个4×4的棋盘分成4个2×2的棋盘, 其中有一个2×2的棋盘存在残缺方格,剩下三个则没有残缺方格。但是只有当棋盘中存在一个残缺方格是,棋盘才能用三格板完全覆盖,所以我们可以为那三个没有残缺方格的棋盘加一个残缺方格,残缺方格不能随便加,下图中灰色的方块便是加的残缺方块,加的三个残缺方块必要能组成一个三格板才行。



代码:
#include <iostream> #include<iomanip> using namespace std; const int MAXSIZE = 100; int tile = 1; int board[MAXSIZE][MAXSIZE]; void chessBoard(int tr, int tc, int dr, int dc, int size) { if(size == 1) return; int t = tile++; int s = size / 2; //覆盖左上角棋盘 if(dr < tr + s && dc < tc + s) {//残缺方格在左上角 chessBoard(tr, tc, dr, dc, s); } else {//此部分无残缺方格,将右下角方格当成残缺方格 board[tr + s - 1][tc + s - 1] = t; chessBoard(tr, tc, tr + s - 1, tc + s - 1, s); } //覆盖右上角棋盘 if (dr < tr + s && dc >= tc + s) {//残缺方格在右上角 chessBoard(tr, tc + s, dr, dc, s); } else {//此部分无残缺方格,将左下角方格当成残缺方格 board[tr + s -1][tc + s] = t; chessBoard(tr, tc + s, tr + s - 1, tc + s, s); } //覆盖左下角棋盘 if (dr >= tr + s && dc < tc + s) {//残缺方格在左下角 chessBoard(tr + s, tc, dr, dc, s); } else {//此部分无残缺方格,将右上角方格当成残缺方格 board[tr + s][tc + s - 1] = t; chessBoard(tr + s, tc, tr + s, tc + s -1, s); } //覆盖右下角棋盘 if (dr >= tr + s && dc >= tc + s) {//残缺方格在右下角 chessBoard(tr + s, tc + s, dr, dc, s); } else {//此部分无残缺方格,将左上角方格当成残缺方格 board[tr + s][tc + s] = t; chessBoard(tr + s, tc + s, tr +s, tc + s, s); } } int main() { int size; cin>>size; int dr, dc; cin >> dr >> dc; chessBoard(0, 0, dr, dc, size); for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) cout << setw(5) << setiosflags(ios::left) << board[i][j]; cout << endl; } return 0; }
输入:
8
1 1
输出:
3 3 4 4 8 8 9 9
3 0 2 4 8 7 7 9
5 2 2 6 10 10 7 11
5 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21
标签:分治 center set cout div 数字 完全 font 位置
原文地址:https://www.cnblogs.com/yichenxing/p/11077053.html