标签:etc cond bre 构造函数 alt 数学 运算 || 指定
昨天写完了T1,T2竟然忘记保存了qaq
T1:Jelly的难题1




真.题面:

这看起来像一个bfs,所以我们就用bfs来做就好了
对于每个是"#"的点来说,高度就是总时间-该点被蔓延到的时间+1,最后一个被蔓延到的点的时间就是总时间。
每个点被蔓延到的时间就是当前出队的点的时间+1
代码:
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> #include<queue> using namespace std; const int mod=19260817; int n,m,sx,sy,hi[509][509],pi[509][509]; char ma[509][509]; int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1},lx,ly; bool vis[509][509]; struct dl{ int x,y; dl(int xx,int yy):x(xx),y(yy){}//构造函数 }; queue <dl> q; int read() { char ch=getchar(); int x=0;bool flag=0; while(ch<‘0‘||ch>‘9‘) { if(ch==‘-‘)flag=1; ch=getchar(); } while(ch>=‘0‘&&ch<=‘9‘) { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } if(flag)x=-x; return x; } bool hf(int xx,int yy) { if(vis[xx][yy])return false; if(ma[xx][yy]==‘o‘)return false; if(xx>n||xx<1||yy>m||yy<1)return false; return true; } void bfs() { while(!q.empty())//一个bfs { dl ex=q.front(); q.pop(); for(int i=0;i<=3;i++) { int xx=ex.x,yy=ex.y; xx+=dx[i];yy+=dy[i]; if(hf(xx,yy)) { pi[xx][yy]=pi[ex.x][ex.y]+1; lx=xx;ly=yy;//记录最后一个被遍历到的点 vis[xx][yy]=1; q.push(dl(xx,yy)); } } } } int main() { n=read();m=read(); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { ma[i][j]=getchar(); while(ma[i][j]!=‘*‘&&ma[i][j]!=‘#‘&&ma[i][j]!=‘o‘)ma[i][j]=getchar();//因为读入有空格,所以要处理(过滤非法字符) if(ma[i][j]==‘*‘) { sx=i;sy=j;//记录起点 } } } vis[sx][sy]=1; q.push(dl(sx,sy)); bfs();int ans=0; for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(ma[i][j]==‘#‘) {hi[i][j]=pi[lx][ly]-(pi[i][j]-1); if(pi[i][j]==0)//这里原本是判断无解的,但题目没有无解情况,所以没有遍历到的点的高度就是0 { hi[i][j]=0; } ans+=hi[i][j]; ans=(ans+mod)%mod; } } } printf("%d\n%d",pi[lx][ly],ans); }
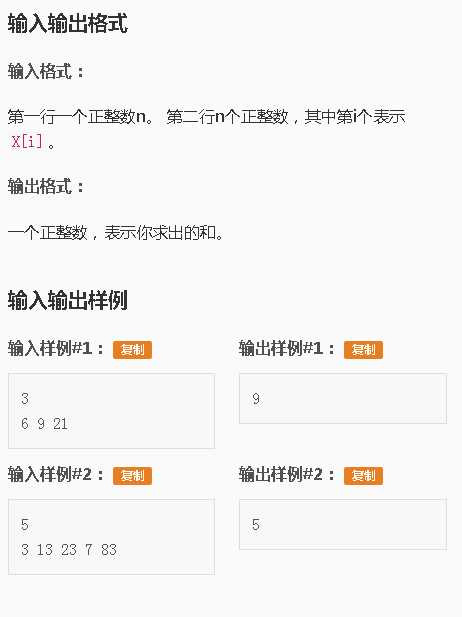
T2:音乐会【二重变革】

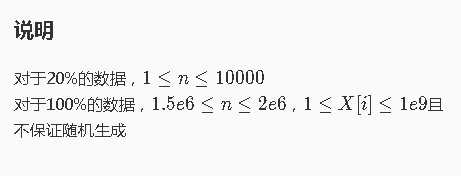
时空限制: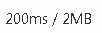
看到这个数据范围,显然直接交上去这个代码它会T的飞起(事实上只有10分)
所以我们要进行一番玄学思考,推理出数学的做法。
我们先分析样例,样例1的三个数的gcd是3,n=3,3*3=9,样例2的所有数的gcd是1,n=5,1*5=5
所以我们求出所有数的gcd,然后乘n,就是答案。
怎么证明?
我们看n=2的情况,这就是更相减损术。
n>2,可以视为n=2+1+1+1+....,所以每读入进来一个x,还是相当于之前用更相减损术求出来的gcd再进行一次更相减损术,所以最后还是gcd(个人证法)
_rqy的证法:

我们再考虑空间限制。显然开数组的话,光存储x数组基本就没有其他空间了,加之一个x求完gcd之后就没有用了,所以我们可以边读入边求,每次读入的x都会覆盖掉上一个x,这样就可以大幅度的节省空间
然后就是ac了
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> #include<queue> using namespace std; int n,x,agcd; int gcd(const int &a,const int &b)//非递归形式,我猜大概可以省空间吧 { int m=a,k=b; while(k) { int r=m; m=k; k=r%k; } return m; } void read(int &x)//据说可以省空间的取地址的快读 { char ch=getchar(); x=0;bool f=0; while(ch<‘0‘||ch>‘9‘) {if(ch==‘-‘)f=1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘) {x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } if(f)x=-x; } int main() { read(n); read(x); agcd=x; for(int i=2;i<=n;i++) { read(x); agcd=gcd(agcd,x); if(agcd==1)break;//节约时间 } printf("%d",agcd*n); return 0; }
T3:音乐会【道路千万条】
OI千万条,暴力第一提条,骗分不规范,爆0两行泪



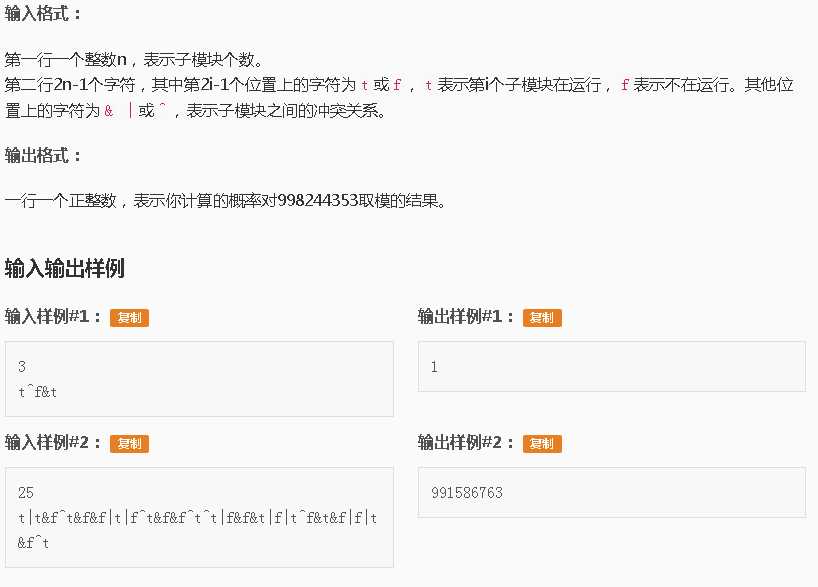

真.题面还是在最后
又是bool表达式问题。
可以想到表达式的值(虽然wz说还有一道加分二叉树也是,但是没见过,不会做,没思路)
我们复习一下关于bool表达式的true与false的关系(下面用t[x]表示x为true的方案数,f[x]表示x为false的方案数)
"&":左右两边同时为真,结果为true,否则为false。t[x&y]=t[x]*t[y],f[x&y]=t[x]*f[y]+f[x]*t[y]+f[x]*f[y]
"|":左右两边只要有一边为真,表达式的值为真,只有当左右两边的值都为假的时候,表达式为假。t[x|y]=t[x]*t[y]+t[x]*f[y]+f[x]*t[y],f[x|y]=f[x]*f[y]
"^"(异或):左右两边相同为假,不同为真。t[x^y]=t[x]*f[y]+f[x]*t[y],f[x^y]=t[x]*t[y]+f[x]*f[y]。
这个题要我们求随机指定顺序的概率。爆搜顺序在大数据面前肯定会挂的。我们可以先确定最后求哪一个运算符,再递归求下一个要计算的运算符。
但据water_lift说递归会炸。
所以就有了下一个思路记忆化搜索。(代码不会啊)
我们也可以搞一个区间dp,分别开两个数组,一个记录当前的字符(t或f),一个记录第i个与第i+1个字符直接的运算符,在dp时根据运算符讨论情况。(具体的式子就是上面推导的辣)
区间dp:第一层枚举区间长度,第二层枚举起点,算出终点,不断更新
考虑到在模意义下做除法,我们还得求逆元。
虽然里面讲了线性筛,但是我只会exgcd(现在连exgcd都快忘辣)
先上wz的代码(自己的还木有搞出来)
#include<bits/stdc++.h> using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<‘0‘||ch>‘9‘) { if(ch==‘-‘)f=1; ch=getchar(); } while(ch>=‘0‘&&ch<=‘9‘) { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } if(f)x=-x; return x; } inline char gc()//忽略无用字符 { char c; do { c=getchar(); } while(c==‘ ‘||c==‘\n‘||c==‘\r‘||c==‘\0‘||c==‘\t‘); return c; } int n; char s[501],ops[501];//s存操作数(t or f),ops存操作符(&,|,^) long long t[501][501],f[501][501];//i到j的true方案数,false的方案数 const int mod=998244353; pair<long long,long long> extgcd(long long a,long long b) { if(b==0) { return make_pair<long long,long long>(1,0); } pair<long long,long long>rtn=extgcd(b,a%b); rtn.first ^=rtn.second^=rtn.first^=rtn.second;//交换两个变量 rtn.second-=a/b*rtn.first; return rtn; } int main() { n=read(); for(int i=1;i<=n-1;i++) { s[i]=gc(); ops[i]=gc(); } s[n]=gc(); for(int i=1;i<=n;i++)//初始化 { if(s[i]==‘t‘) t[i][i]=1,f[i][i]=0; else f[i][i]=1,t[i][i]=0; } for(int len=2;len<=n;len++)//区间dp枚举区间长 { for(int i=1;i+len-1<=n;i++)//枚举起点 { int j=i+len-1;//计算终点 for(int k=i;k<j;k++)//枚举断点 { if(ops[k]==‘&‘) { t[i][j]=(t[i][j]+(t[i][k]*t[k+1][j])%mod)%mod;//为‘&‘,true为左右两边都必须是true f[i][j]=(f[i][j]+(f[i][k]*f[k+1][j])%mod+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod)%mod; //false:左右都是false,左false右true,左true右false } if(ops[k]==‘|‘) { t[i][j]=(t[i][j]+(t[i][k]*t[k+1][j])%mod+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod)%mod; //true:两端true,左true右false,左false右true f[i][j]=(f[i][j]+(f[i][k]*f[k+1][j])%mod)%mod; //false:两端都false } if(ops[k]==‘^‘) { t[i][j]=(t[i][j]+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod)%mod; //true:左false右true,左true右false(两端不同) f[i][j]=(f[i][j]+(t[i][k]*t[k+1][j])%mod+(f[i][k]*f[k+1][j])%mod)%mod; //false:左true右true,左false右false(两边不同) } } } } cout<< (t[1][n] * ((extgcd(t[1][n] +f[1][n] %mod, mod).first%mod+mod) %mod)) %mod<<endl;//t(1,n)/(t(1,n)+f(1,n)) % mod }
标签:etc cond bre 构造函数 alt 数学 运算 || 指定
原文地址:https://www.cnblogs.com/lcez56jsy/p/11105752.html