标签:des style http color io os ar java for
Galaxy
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 553 Accepted Submission(s): 126
Special Judge
Problem Description
Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.
To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.
Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.
The moment of inertia I of a set of n stars can be calculated with the formula
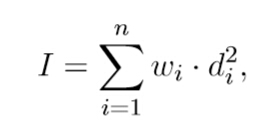
where w
i is the weight of star i, d
i is the distance form star i to the mass of center.
As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial
pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.
Now, you are supposed to calculate the minimum moment of inertia after transportation.
Input
The first line contains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.
Output
For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.
Sample Input
2
3 2
-1 0 1
4 2
-2 -1 1 2
Sample Output
题意:数轴上有n个点,每个点重量1 ,可以移动其中k个点到任何位置, 使得题中式子值最小
di表示第i个点距离现在n个点的重心(即平均距离)的距离。
思路:选择区间长度为N - K的连续的数, 然后其余的K个数都移动到这N-K个数的中心就可以。
区间长度为 t = N - K的连续的数的值: p=(a[i]-x)*(a[i] - x)+ (a[i+1] - x)*(a[i+1]
- x)
+ ......+(a[t-1+i]-x)*(a[t-1+i]-x);(其中x为平均距离)
p = (a[i]*a[i] +a[i+1]*a[i+1] +......+a[t-1+i]*a[t-1+i]) - 2*x*(a[i]+a[i+1]+......+a[ t-1+i ] ) + t*x*x ;
令sum1[ i ] 表示a数组前i项的平方和,sum2[ i ] 表示a数组前i项的和;
即 x=(sum2[ t+i-1 ]-sum2[ i -1 ] )/ t ;
sum1[ t+i-1 ]-sum1[ i -1 ] = a[i]*a[i] +a[i+1]*a[i+1]
+......+a[t-1+i]*a[t-1+i] ;
sum2[ t+i-1 ]-sum2[ i -1 ] = a[i]+a[i+1]+......+a[t-1+i]
;
所以 p = sum1[ t+i-1 ]-sum1[ i -1 ] - (sum2[ t+i-1 ]-sum2[ i -1 ] )*(sum2[
t+i-1 ]-sum2[ i -1 ] )/ t ;
然后枚举 i ,算出最小的即为答案 。 (注意精度问题)
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
const int maxn=50050;
double sum1[maxn],sum2[maxn],a[maxn];
int n,k;
void input()
{
scanf("%d %d",&n,&k);
for(int i=1; i<=n; i++) scanf("%lf",&a[i]);
}
void solve()
{
double ans;
if(k==n) ans=0.0;
else
{
sort(a+1,a+n+1);
sum1[0]=sum2[0]=0.0;
for(int i=1; i<=n; i++)
{
sum1[i]=sum1[i-1]+a[i]*a[i];
sum2[i]=sum2[i-1]+a[i];
}
int t=n-k;
for(int i=1; i+t<=n+1; i++)
{
double p=sum1[i+t-1]-sum1[i-1]-(sum2[i+t-1]-sum2[i-1])*(sum2[i+t-1]-sum2[i-1])/t;
if(i==1) ans=p;
else ans=min(ans,p);
}
}
printf("%.9lf\n",ans);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
input();
solve();
}
return 0;
}
hdu 5073 Galaxy (数学+推导)
标签:des style http color io os ar java for
原文地址:http://blog.csdn.net/u012596172/article/details/40386979