标签:const user inline 需要 也有 cal lin 最小 英文
模板题,无背景。
定义积性函数$f(x)$,且$f(p^k)=p^k(p^k-1)$($p$是一个质数),求
$$\sum_{i=1}^n f(x)$$
对$10^9+7$取模。
一行一个整数$n$。
输出格式:一个整数表示答案。
$f(1)=1,f(2)=2,f(3)=6,f(4)=12,f(5)=20$
$f(6)=12,f(7)=42,f(8)=56,f(9)=72,f(10)=40$
对于$30\%$的数据,保证$1\le n\le 10^6$。
对于$100\%$的数据,保证$1\le n\le 10^{10}$
求\(\sum_{i=1}^nf(i)\),其中\(f(i)\)是一个积性函数,且\(f(p^k)=p^k(p^k-1)\)。
为什么这个筛法叫做Min25筛呢?因为这个算法是Min25发明的。
假设我们要求一个\(\sum_{i=1}^nf(i)\),满足\(f(x)\)是一个积性函数,且\(f(p^e)\)是一个关于\(p\)的低阶多项式。
因为多项式可以拆成若干个单项式,所以我们只需要考虑求出\(f(p)=p^k\)的前缀和,然后每一项加起来就行了。
那么如何求出每一项的和呢?
\[\sum_{i=1}^nf(i)=\sum_{1\le p\le n}f(p)+\sum_{i=1\&\text{i is not a prime}}^nf(i)\]
然后,我们枚举后面合数的最小质因子以及最小质因子的次数。注意所有合数的最小质因子一定都小于等于\(\sqrt n\):
\[\sum_{1\le p\le n}f(p)+\sum_{1\le p^e\le n,1\le p\le \sqrt n}f(p^e)\left(\sum_{1\le i\le n/p^e\&minp>p}f(i)\right)\]
其中\(minp\)表示\(i\)的最小质因子,因为公式中文太丑了所以就只好写英文了。
这样,整个式子就变成了两个部分,第一部分是所有质数的\(f\)之和,另一部分是枚举最小质因子后,求所有最小质因子大于这个质因子的\(f\)之和。
我们考虑一个DP的思路(天哪这是怎么想到的):我们不知道从哪里找来了一个DP数组\(g(n,i)\),满足
\[g(n,j)=\sum_{i=1}^n[\text{i is a prime or minp$> p_j$}]i^k\]
这里的\(k\)就是前面我们说的低阶多项式的一项(此题中\(k\in\{1,2\}\))。注意\(i^k\)并不是我们要求的\(f\),只是一个和\(f\)在质数处的取值一样的完全积性函数,这样后面计算起来比较方便。
这个式子说人话就是\(g(n,j)\)表示求\(1\)到\(n\)之间所有满足条件的数的\(k\)次方和,条件就是要么是质数要么最小质因子大于\(p_j\)。
我们考虑\(g(n,j-1)\)如何转移到\(g(n,j)\)。随着\(j\)的增大,满足条件的数变少了,所以我们需要减去一些原来满足条件而现在不满足条件的数。
这些数应该是最小质因子恰好为\(p_{j}\)的合数。
我们可以提出来一个\(p_{j}\)作为最小质因子,这样剩下的就不能有小于它的质因子了,也就是\(g\left(\dfrac{n}{p_{j}},j\right)-g(p_{j-1},j-1)\),后面那个\(g\)是为了把所有的质数去掉。
这样我们就得到了\(g\)的递推式:
\[g(n,j)=g(n,j-1)-p_j^k\left(g\left(\dfrac{n}{p_j},j\right)-g(p_{j-1},j-1)\right)\]
完全积性函数的好处在这里就体现出来了:由于只提出了一个\(p_i\),所以后面还有可能有\(p_i\)这个因子,如果是完全积性函数的话就可以将函数值直接相乘,而不用管是否互质。
注意到后面的\(g(p_{j-1},j-1)\)其实就是前\(j-1\)个质数的\(k\)次方和。由于\(p_j\le \sqrt n\),所以这一部分可以用线性筛预处理,我们设\(sp_n=\sum_{i=1}^np_i^k\),也就是前\(n\)个质数的\(k\)次方和。
\(1\)到\(n\)中所有质数的\(k\)次方和其实就是\(g(n,x)\),其中\(p_x\)是最后一个小于等于\(\sqrt n\)的质数。为了方便,我们把它记作\(g(n)\)。
但是因为\(n\)太大,我们还是没法对于每一个\(n\)求出\(g(n,x)\),所以我们可以想到另一个重要的结论:
\[\left\lfloor\dfrac{\lfloor\dfrac na\rfloor}{b}\right\rfloor=\lfloor\dfrac{n}{ab}\rfloor\]
也就是说,无论你每一次把\(n\)除以几,最后你能得到的数一定是某一个\(\lfloor\dfrac nx\rfloor\),所以我们没必要算出来所有的\(n\),只需要算出可以写成\(\lfloor\dfrac{n}{x}\rfloor\)这种形式的数,这样的数一共有\(O(\sqrt n)\)个。
那么我们如何存储这\(\sqrt n\)个数呢?
首先我们不能直接下标访问,这样下标可以到\(n\)。我们需要对下标离散化。
但是离散化之后,我们还需要知道对于每一个\(\lfloor\dfrac nx\rfloor\),它对应的下标是什么。
如果偷懒的话可以用map,但是时间复杂度会多一个\(\log\)。我们可以用\(ind1[x]\)表示\(x\)这个数对应的数组下标,\(ind2[x]\)表示\(n/x\)这个数对应的下标。这样两个\(ind\)数组最大都只会到\(\sqrt n\)。
具体实现可以看代码。数组的记录上需要精细实现一下。
我们还是可以考虑DP的思想。设\(S(n,x)\)表示求\(1\)到\(n\)中所有最小质因子大于\(p_x\)的函数值之和,注意这里是\(f\)而不是\(k\)次方。答案就是\(S(n,0)\)。
我们将满足条件的数分成两部分,第一部分是大于\(p_x\)的质数,也就是\(g(n)-sp_x\),另一部分是最小质因子大于\(p_x\)的合数,枚举最小质因子:
\[S(n,x)=g(n)-sp_x+\sum_{p_k^e\le n\&k>x}f(p_k^e)\left(S\left(\dfrac{n}{p_k^e},k\right)+[e\neq 1]\right)\]
这样问题就解决了,我们可以递归求解这个问题。根据某玄学定理,不需要记忆化。
一些细节
\(1\)既不是质数也不是合数,不含任何一个质因子,那么求解的过程中\(g\)和\(S\)到底是否包含\(1\)呢?其实是否包含都可以,但是处理上略有差别。我的\(g\)和\(S\)都没有包含\(1\),只需要最后加一就行了。
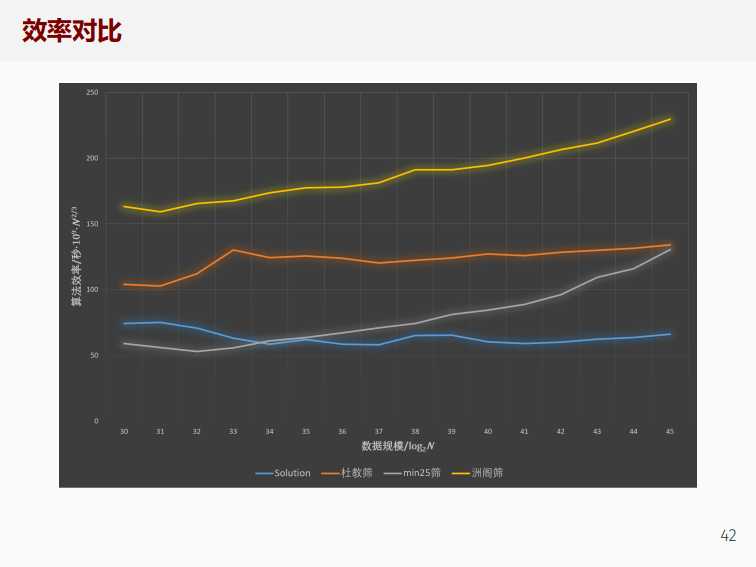
min25筛的时间复杂度据说是\(O\left(\dfrac{n^{3/4}}{\log n}\right)\),也有人说是\(O(n^{1-\epsilon})\),在这道题上大致是1e10跑1s左右的样子。但是这个算法常数很小,具体表现参加WC2019课件里面的一张图:(灰色的是min25)
#include<bits/stdc++.h>
#define il inline
#define co const
template<class T>T read(){
T data=0,w=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
return data*w;
}
template<class T>il T read(T&x) {return x=read<T>();}
typedef long long LL;
using namespace std;
co int mod=1e9+7,i2=500000004,i6=166666668;
il int add(int a,int b){
return (a+=b)>=mod?a-mod:a;
}
il int mul(int a,int b){
return (LL)a*b%mod;
}
//int fpow(int a,int b){ // calc inv
// int ans=1;
// for(;b;b>>=1,a=mul(a,a))
// if(b&1) ans=mul(ans,a);
// return ans;
//}
co int N=2e5+1; // edit 1: size
LL n;
int sqr,pri[N],num,sp1[N],sp2[N];
LL w[N];int tot,g1[N],g2[N],ind1[N],ind2[N];
void init(){
pri[1]=1;
for(int i=2;i<=sqr;++i){
if(!pri[i]){
pri[++num]=i;
sp1[num]=add(sp1[num-1],i);
sp2[num]=add(sp2[num-1],mul(i,i));
}
for(int j=1;j<=num&&i*pri[j]<=sqr;++j){
pri[i*pri[j]]=1;
if(i%pri[j]==0) break;
}
}
}
int S(LL x,int y){
if(pri[y]>=x) return 0;
int k=x<=sqr?ind1[x]:ind2[n/x];
int ans=add(add(g2[k],mod-g1[k]),mod-add(sp2[y],mod-sp1[y]));
for(int i=y+1;i<=num&&(LL)pri[i]*pri[i]<=x;++i){
LL p=pri[i];
for(int e=1;p<=x;++e,p=p*pri[i]){
int t=p%mod;
ans=add(ans,mul(t,mul(t-1,add(S(x/p,i),e!=1))));
}
}
return ans;
}
int main(){
sqr=ceil(sqrt(read(n))),init();
// part 1
for(LL l=1,r;l<=n;l=r+1){ // init g(w,0)
r=n/(n/l);
w[++tot]=n/l; // big->small
g1[tot]=g2[tot]=w[tot]%mod;
g1[tot]=mul(i2,mul(g1[tot],g1[tot]+1)),g1[tot]=add(g1[tot],mod-1);
g2[tot]=mul(i6,mul(g2[tot],mul(g2[tot]+1,2*g2[tot]+1))),g2[tot]=add(g2[tot],mod-1);
if(n/l<=sqr) ind1[n/l]=tot;
else ind2[n/(n/l)]=tot;
}
for(int i=1;i<=num;++i) // DP g(w,i)
for(int j=1;j<=tot&&(LL)pri[i]*pri[i]<=w[j];++j){
int k=w[j]/pri[i]<=sqr?ind1[w[j]/pri[i]]:ind2[n/(w[j]/pri[i])];
g1[j]=add(g1[j],mod-mul(pri[i],add(g1[k],mod-sp1[i-1])));
g2[j]=add(g2[j],mod-mul(pri[i],mul(pri[i],add(g2[k],mod-sp2[i-1]))));
}
// part 2
printf("%d\n",add(S(n,0),1));
return 0;
}这题数组空间,我开刚好\(\sqrt{n}\),也就是1e5,就会炸掉。试了一下开到2e5才过。大概是数据有问题。
标签:const user inline 需要 也有 cal lin 最小 英文
原文地址:https://www.cnblogs.com/autoint/p/11113256.html