计算机组成原理(科学出版社) 第二章：运算方法和运算器

标签：就是   n+1   back   ima   补全   总线   sla   常用   src   

复习

20190630

一、 原码、补码、反码、移码

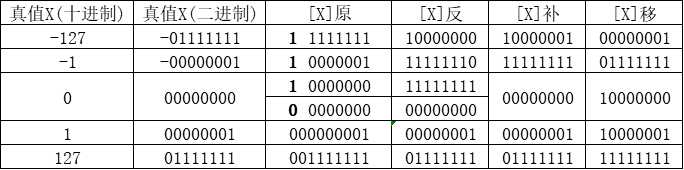
真值(十进制数) 转换为真值(二进制数)最好补全为八位，对应的原码就是将最高位写成符号位(还是八位)

具体思维导图如下：

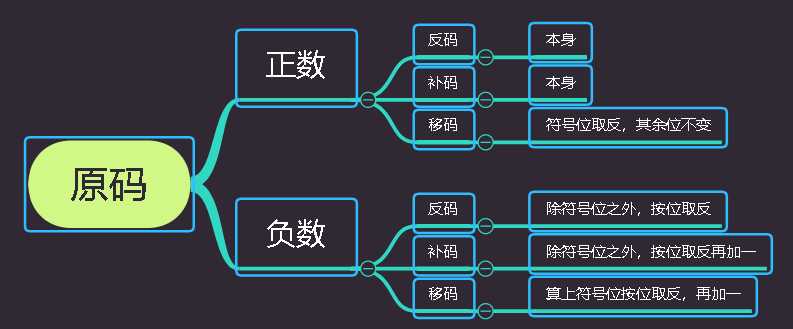
原码求补码的简便方法：除符号位之外，从最低位开始，遇第一个1之前的各位保持不变，其余各位按位取反

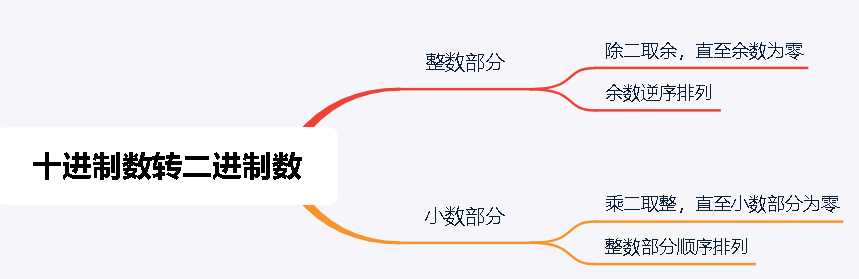
进制之间的转换，思维导图如下：

二、补码加减法

1. 补码加法公式：[X]补 + [Y]补 = [X+Y]补    (mod  2n+1)

定理：任意两数补码之和等于该两数之和的补码

2.  补码的乘法和除法就是将[X]的补码向左或者右移位一次，符号位移走之后照原来的补上，这就是算术移位。

算术移位：

由[X]补求[X/2]补

—  [X]补    =   10101000

—  [X/2]补 =    110101000

3. 补码的减法公式：[X — Y]补 = [X]补 — [Y]补 = [X]补 + [—Y]补

又知道，[—Y]补 等于[Y]补 取反，末位加1，所以可化为加法运算

4. 注意检测溢出，单双符号位

三、 定点运算器

1. 逻辑运算

(1). 逻辑非

• 逻辑非又叫求反，按位取反

(2). 逻辑加

• 逻辑加又叫逻辑或，常用+来表示

(3). 逻辑乘 

• 逻辑乘又叫逻辑与，常用 。来表示 

(4). 逻辑异

• 对两数进行逻辑异就是按位求他们的模2和，所以逻辑异又称为按位加，常用记号来表示

2. 多功能算术/逻辑运算单元ALU

(1). 串行加法器的不足:速度慢

(2). ALU的设计思想：

• 增加函数发生器
• 增加逻辑运算功能
• 增加先行进位

(3). 多功能算术/逻辑运算单元ALU（四）——总体设计

• 单级先行进位方式：片内先行进位，片间串行进位。
• 两级先行进位方式：片内先行进位，片间先行进位。

3. 内部总线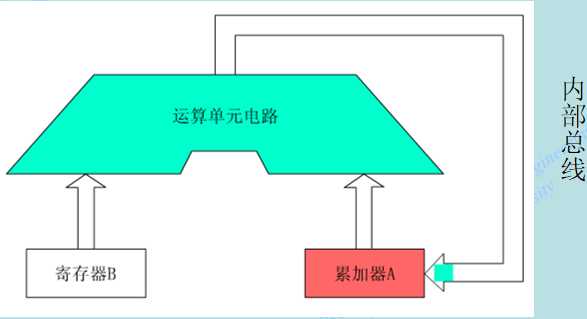

4. 定点运算器的基本结构

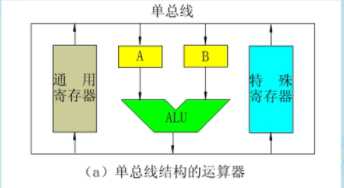
（1）. 单总线结构的运算器

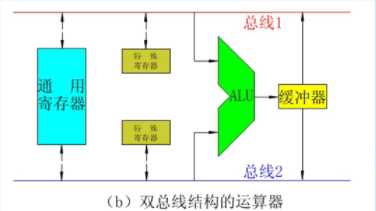
（2）. 双总线结构的运算

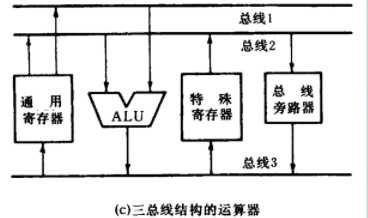
（3）. 三总线结

六、 浮点运算器

(1). 浮点加减法运算  (重点)

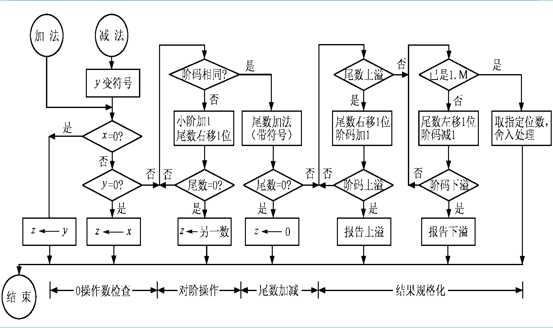
运算步骤如下：

1. 0操作数的检查，看有无简化操作的可能

2. 比较阶码大小并完成对阶(小阶向大阶对齐)；

3. 尾数进行加减运算

4. 结果规格化并进行舍入处理

       注：

• • 浮点数中  零操作数的含义：当一个浮点数的尾数为0，则不论其阶码为多少，该浮点数的值都为0.
  • 当阶码的值遇到比它所能表示的最小数还小的值时，不管尾数现在值是多少，计算机都把该浮点数看成0，通常叫做机器0，这时计算机一般将该浮点数的所有各位清0。

浮点数规格化的定义是1/2≤|M|<1，显然，是真值的规格化。变成码制就不一定是规格化的数了。采用双符号位时，对正数有M=00.1øø…ø。对于负数，其补码形式为11.0øø…ø。可见，只要对运算结果的符号位和小数点后的第一位进行比较，如果他们不等，即为00.1øø…ø或11.0øø…ø，就是规格化数；如果他们相等，即00.0øø…ø或11.1øø…ø，就不是规格化数，这种情况下，尾数左移实现规格化，叫向左规格化，规则为：尾数左移1位，阶码减1。

当出现01. øø…ø或10.øø…ø时，在定点数中是溢出，但浮点数中则是非规格化数，表示结果绝对值大于1。此时需向右规格化，规则为：尾数右移一位，阶码加1。

无论左移还是右移，符号位保持不变。

(2). 浮点乘除法运算

(3). 对阶小数点

(4). 尾数求和

(5). 防溢出

(6). 结果规划

计算机组成原理(科学出版社) 第二章：运算方法和运算器

标签：就是   n+1   back   ima   补全   总线   sla   常用   src   

原文地址：https://www.cnblogs.com/yuandongshisan/p/11110887.html