标签：向量   mda   存在   使用   类别   auto   有一个   样本   事件   

贝叶斯决策

贝叶斯公式（后验概率）：

• p(w)：每种类别分布的概率——先验概率；
• p(x|w)：某类别下x事件发生的概率——条件概率；
• p(w|x)：x事件已经发生，属于某类的概率——后验概率；
  • 后验概率越大，说明x事件属于这个类的概率越大，就越有理由把事件x归到这个类下

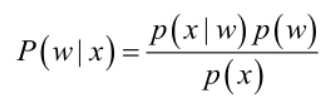
实际问题中，我们只知道优先数目的样本数据，先验概率和条件概率不知道，求不出后验概率。这个时候需要对先验概率和条件概率进行估计，然后再使用贝叶斯分类器。

先验概率的估计方法：

1. 每个样本的属于哪个类是已知的（有监督学习）；
2. 依靠经验；
3. 用训练样本中各类出现的频率估计；

后验概率的估计（很难）：

概率密度函数包含的信息很多，样本数据不多，特征向量维度很大，所以估计这个概率密度函数很难。

因此将概率密度函数的估计转化为估计参数，就是极大似然估计。

当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值，如果模型都错了，那估计半天的参数，肯定也没啥意义了。

前提

使用极大似然估计的前提：

训练样本的分布能代表样本的真实分布；每个样本集中的样本都是独立同分布的随机变量；有充分的训练样本。

极大似然估计

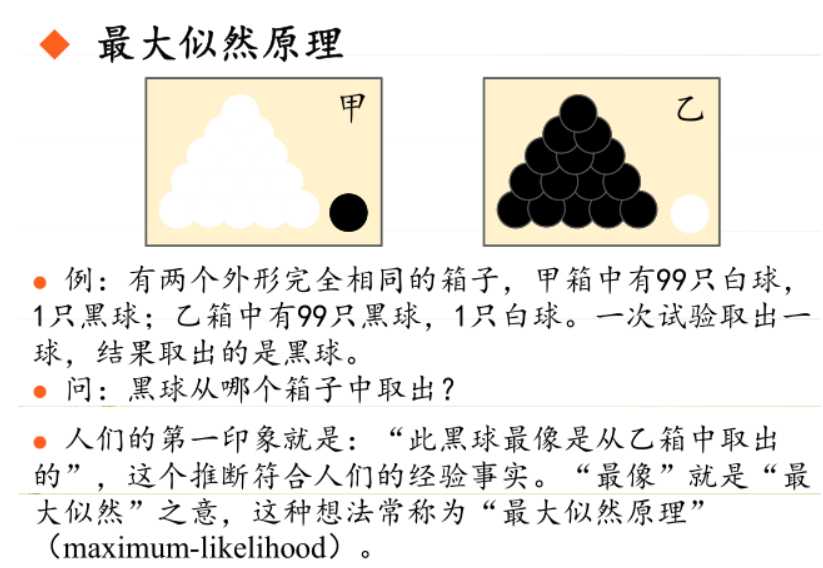
模型已定，参数未知：利用已知的样本结果，反推最有可能（最大概率）导致这种结果的参数值。

通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

由于样本集中的样本都是独立同分布，可以只考虑一类样本集D，来估计参数向量θ。记已知的样本集为：

似然函数（linkehood function）：

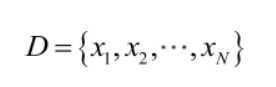
联合概率密度函数称为相对于样本集的θ的似然函数。

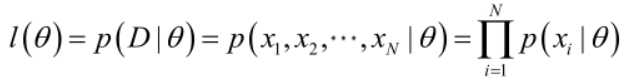
如果存在一个参数值θ使得整个似然函数得到最大值，那么这个θ就是极大似然估计量，他是样本集的函数：

求解极大似然函数

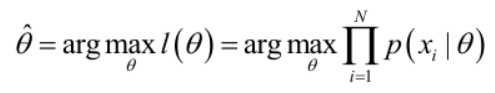
实际中为了便于分析，定义了对数似然函数：

1. 未知参数只有一个（θ为标量）：

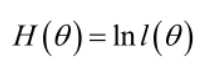
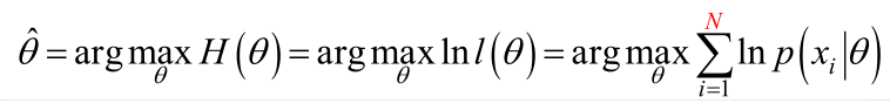
在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：

2.未知参数有多个（θ为向量）

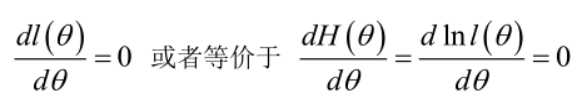
则θ可表示为具有S个分量的未知向量：

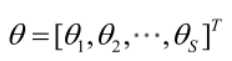
记梯度算子：

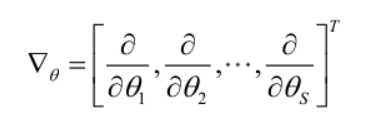
若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解：

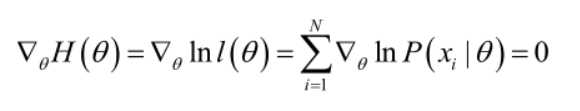
方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。

特点：

简单，收敛性好，样本数目越多收敛性能越好；依赖模型，如果模型就是错的，那么估计出的参数肯定也是错的，最后的结果会很差。

贝叶斯————极大似然估计

标签：向量   mda   存在   使用   类别   auto   有一个   样本   事件   

原文地址：https://www.cnblogs.com/pacino12134/p/11114314.html