标签:否则 ofo 不为 特点 一个 image 特殊 图片 tree
一、树的定义树的定义
?树是一种非线性的数据结构
?树是由 n (n≥0) 个结点组成的有限集合
??如果 n = 0,称为空树 ;
??如果 n > 0,则 :
???有一个特定的称之为根 (root) 的结点,它只有直接后继,但没有直接前驱
???除根以外的其它结点划分为 m (m≥0) 个互不相交的有限集合T0, T1, …,Tm-1, 每个集合又是一棵树, 并且称之为根的子树(subTree)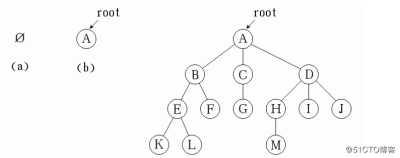
树家族中的概念
?树的结点包含一个数据及若干指向子树的分支
?结点拥有的子树数称为结点的度
??度为0的结点称为叶结点
??度不为0的结点称为分支结点
?树的度定义为所有结点中的度的最大值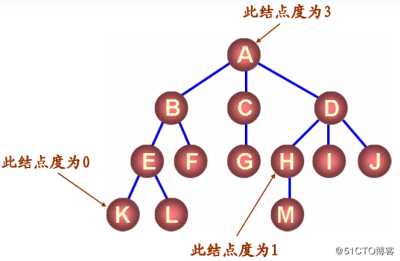
?结点的直接后继称为该结点的孩子
??相应的,该结点称为孩子的双亲
?结点的孩子的孩子的…… 称为该结点的子孙
??相应的,该结点称为子孙的祖先
?同一个双亲的孩子之间互称兄弟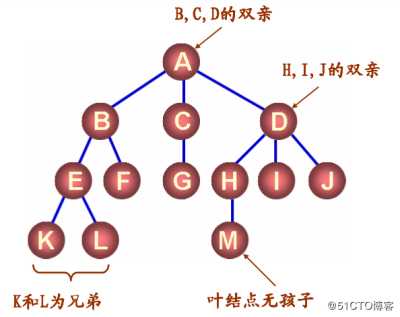
?结点的层次
??根为第1层
??根的孩子为第2层
? ?……
?树中结点的最大层次称为树的深度或高度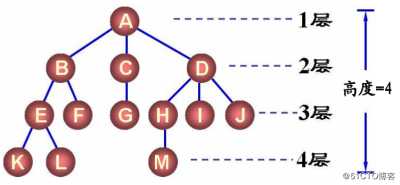
如果树中结点的各子树从左向右是有次序的,子树间不能互换位置 ,则称该树为有序树 ,否则为无序树。
森林是由 n ( n≥0) 棵互不相交的树组成的集合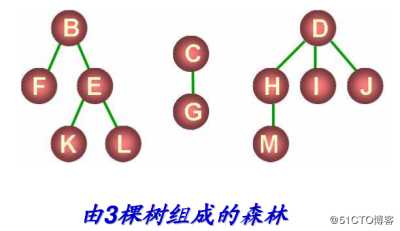
树的一些常用操作
创建树
销毁树
清空树
插入结点
删除结点
获取结点
获取根结点
获取树的结点数
获取树的高度
获取树的度
树的存储结构
?无法直接用数组表示树的逻辑结构
?但可以设计结构体数组对结点间的关系进行表述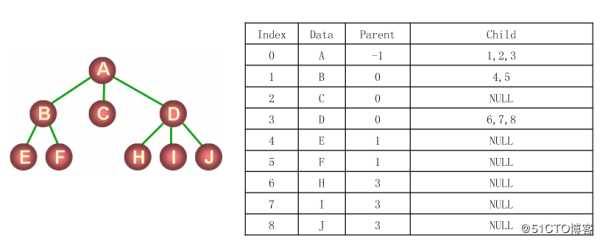
利用链表组织树中的各个结点
链表中的前后关系不代表结点间的逻辑关系
结点的逻辑关系由 child 数据域描述
child 数据域保存其他结点的存储地址
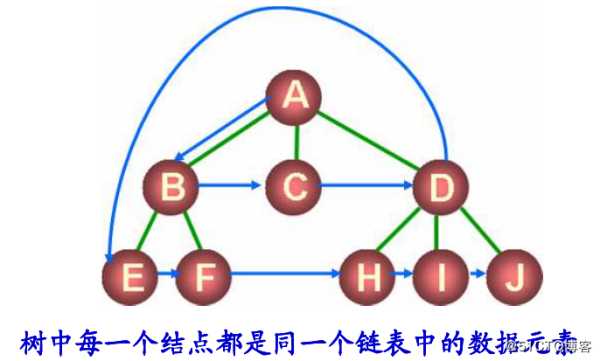
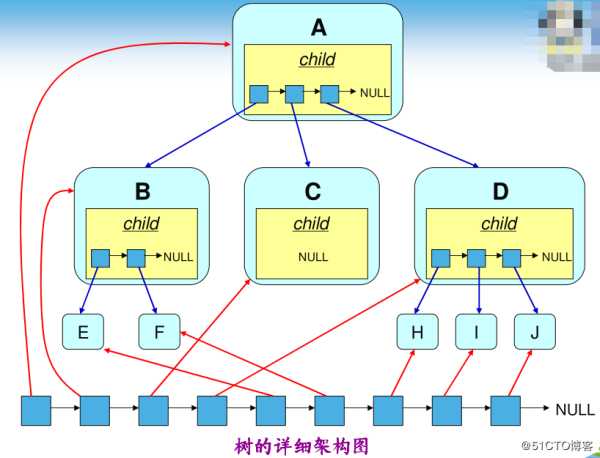
另一种树结构模型
孩子兄弟表示法模型
?每个结点都有一个指向其第一个孩子的指针
?每个结点都有一个指向其第一个右兄弟的指针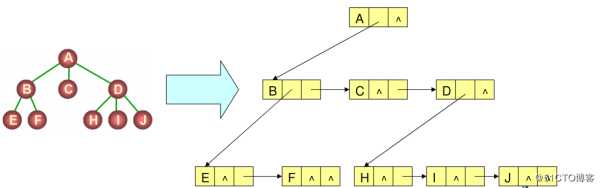
每个结点包含一个数据指针和两个结点指针
?数据指针 : 指向保存于树中的数据
?孩子结点指针 : 指向第一个孩子
?兄弟结点指针 : 指向第一个右兄弟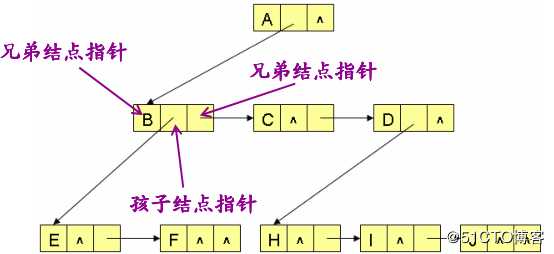
孩子兄弟表示法的特点
?能够表示任意的树形结构
?每个结点中有且仅有三个指针域
??数据指针,孩子结点指针,兄弟结点指针
?每个结点的结构简单
??只有孩子结点指针和兄弟结点指针构成了“树杈"
二叉树的定义
二叉树是由n ( n ≥0) 个结点组成的有限集合, 该集合或者为空, 或者是由一个根结点加上两棵分别称为左子树和 右子树的 、 互不相交的二叉树组成。
特殊的二叉树
满二叉树(Full Binary Tree)
如果 二叉树中所有分支结点的度数都为2, 且叶子结点都在同一层次上 , 则称这类二叉树为满二叉树 。
完全二叉树 (Complete Binary Tree)
如果一棵具有n个结点的高度为k的二叉树, 它的每一个结点都与高度为k 的满二叉树中编号为1—n 的结点一一对应, 则称这棵二叉树为完全二叉树。(从上到下从左到右编号)
完全二叉树的叶结点仅出现在最下面两层
??最下层的叶结点一定出现在左边
??倒数第二层的叶结点一定出现在右边
?完全二叉树中度为1的结点只有左孩子
?同样结点数的二叉树 , 完全二叉树的高度最小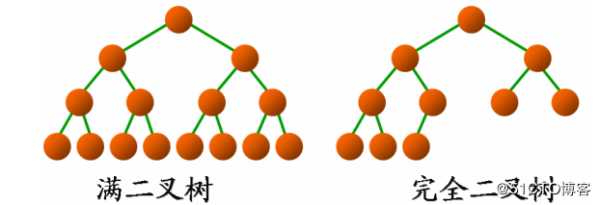
通用树实现源码
标签:否则 ofo 不为 特点 一个 image 特殊 图片 tree
原文地址:https://blog.51cto.com/yinsuifeng/2416183